Problems
Let \(n\) be a positive integer. Prove that it’s impossible to have a closed knight’s tour on a \(4\times n\) grid.
Find an open knight’s tour on a \(2\times2\times2\) cube.
Let \(s\) and \(t\) be two positive integers. Can we have \(s^2=t^2+2\)?
Eleven sages were blindfolded and on everyone’s head a cap of one of \(1000\) colours was put. After that their eyes were untied and everyone could see all the caps except for their own. Then at the same time everyone shows the others one of the two cards – white or black. After that, everyone must simultaneously name the colour of their caps. Will they succeed?
The recertification of the Council of Sages takes place as follows: the king arranges them in a column one by one and puts on a cap of white or black colours for each. All the sages see the colours of all the caps of the sages standing in front, but they do not see the colour of their own and all those standing behind. Once a minute one of the wise men must shout one of the two colours. (each sage shouts out a colour once). After the end of this process the king executes every sage who shouts a colour different from the colour of his cap. On the eve of the recertification all one hundred members of the Council of Sages agreed and figured out how to minimize the number of those executed. How many of them are guaranteed to avoid execution?
At the elections to the High Government every voter who comes, votes for himself (if he is a candidate) and for those candidates who are his friends. The forecast of the media service of the mayor’s office is considered good if it correctly predicts the number of votes at least for one of the candidates, and not considered good otherwise. Prove that for any forecast voters can show up at the elections in such a way that this forecast will not be considered good.
Prove Sperner’s lemma in dimension \(1\), namely on a line.
The simplex in this case is just a segment, the triangulation is
subdivision of the segment into multiple small segments, and the
conditions of a Sperner’s coloring are the following:
There are only two colors;
The opposite ends of the main segment are colored differently;
Then one needs to prove that there exists a small segment with two ends colored in different colors. In particular there is an odd number of such small segments.
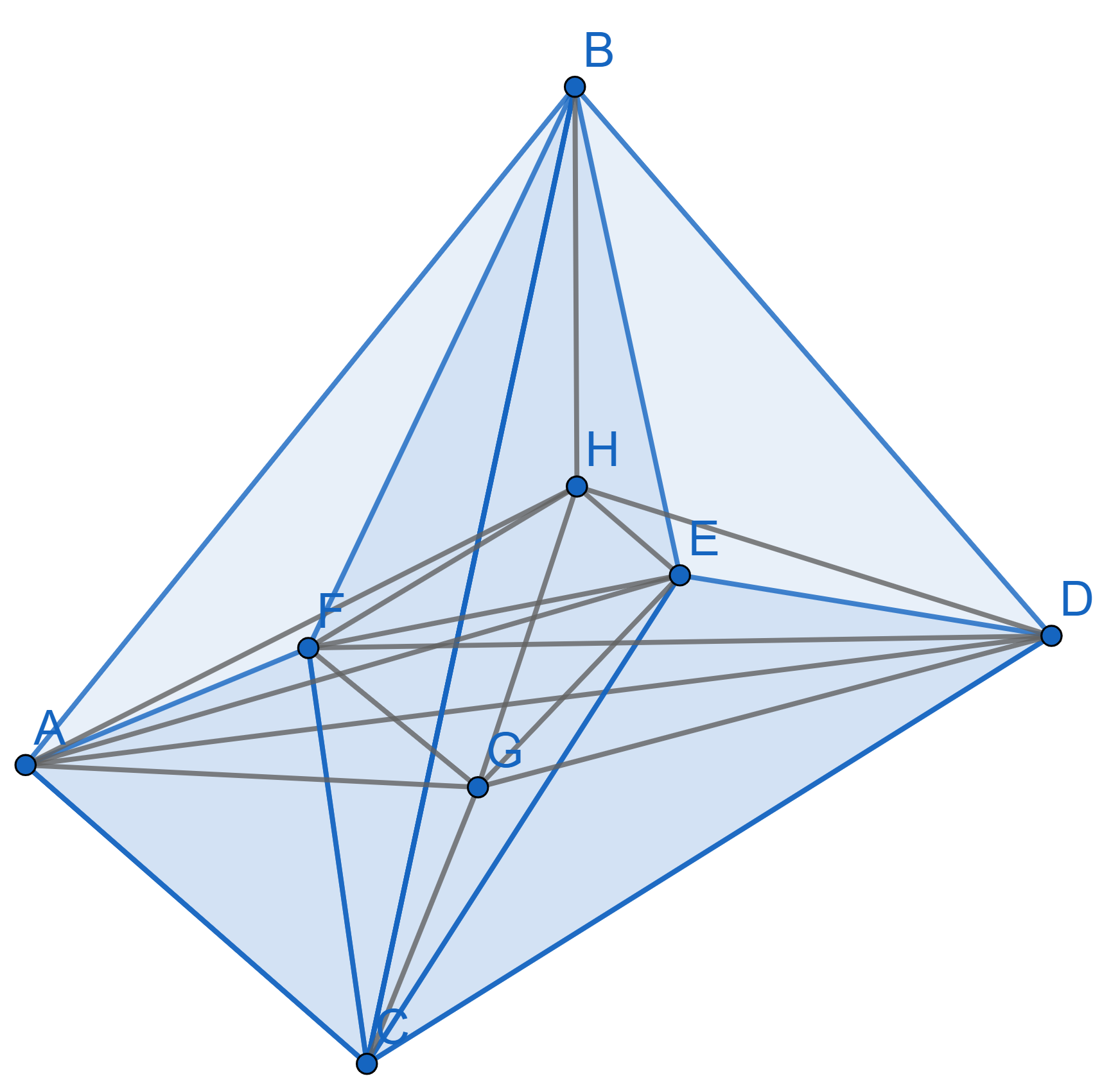
Draw a Sperner’s coloring for the following \(3\)-dimensional simplex. The blue segments are visible, the grey ones are inside the tetrahedron. The point \(F\) is on the face \(ABC\), point \(E\) is on the face \(BCD\), point \(G\) is on the face \(ACD\) and the point \(H\) is on the face \(ABD\).
Four football teams play in a tournament. There’s the Ulams (\(U\)), the Vandermondes (\(V\)), the Wittgensteins (\(W\)) and the Xenos (\(X\)). Each team plays every other team
exactly once, and matches can end in a draw.
If a game ends in a draw, then both teams get \(1\) point. Otherwise, the winning team gets
\(3\) points and the losing team gets
\(0\) points. At the end of the
tournament, the teams have the following points totals: \(U\) has \(7\), \(V\)
has \(4\), \(W\) has \(3\) and \(X\) has \(2\).
Work out the results of each match, including showing that there’s no other way the results could have played out.
Naomi and Rory get tired of playing Nim, so decide to change the rules to mix it up. They call their new variant ‘Wonim’. There are two piles of four matchsticks each. They take it in turns to take matchsticks. Each player has to take at least one matchstick, and they can take as many as they like from one pile only.
Except, their new rule is that a player cannot take the same number of matchsticks that their opponent just did. For example, consider Wonim(\(5\),\(10\)). If Naomi’s first move is to take \(4\) matchsticks from the pile of size \(5\), turning the game to Wonim(\(1\),\(10\)), then Rory cannot take \(4\) matchsticks - he has to take more or less. A player loses if they cannot go - this can happen if there are no matchsticks left, or if there are matchsticks left, but they can’t take any since their opponent took that number. e.g. Wonim(\(1\),\(1\)), Naomi takes \(1\), Rory faces Wonim(\(1\)) but can’t move since he’s not allowed to take \(1\).
In the game Wonim(\(4\),\(4\)) with Naomi going first, who has the winning strategy?