Problems
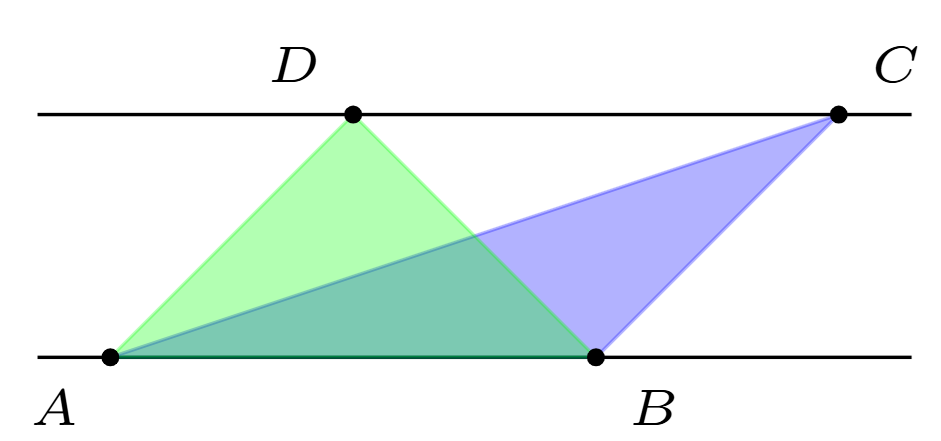
There is a pair of parallel lines. The point \(A\) and \(B\) lie on one of the lines. The point \(C\) and \(D\) lies on the other line. We can form triangles \(\triangle ABC\) and \(\triangle ABD\). Prove that the areas of triangles \(\triangle ABC\) and \(\triangle ABD\) are equal.
What’s the sum of the Fibonacci numbers \(F_0+F_1+F_2+...+F_n\)?
What’s the sum \(\frac{F_2}{F_1}+\frac{F_4}{F_2}+\frac{F_6}{F_3}+...+\frac{F_{18}}{F_9}+\frac{F_{20}}{F_{10}}\)?
We have a sequence where the first term (\(x_1\)) is equal to \(2\), and each term is \(1\) minus the reciprocal of the previous term (which we can write as \(x_{n+1}=1-\frac{1}{x_n}\)).
What’s \(x_{57}\)?
Let \(n\) be a positive integer. Can \(n^7-77\) ever be a Fibonacci number?
There is a very, very fast way of computing the greatest common divisor of two positive integers. It was in fact known even to the Greeks two thousand years ago. This procedure is called the Euclidean algorithm, named after Euclid, a famous ancient Greek mathematician.
The algorithm works as follows. Take two positive integers \(a,b\). Let’s say \(a\geq b\).
Calculate the remainder of \(a\) when divided by \(b\). Call it \(r_1\).
Calculate the remainder of \(b\) when divided by \(r_1\). Call it \(r_2\).
Calculate the remainder of \(r_1\) when divided by \(r_2\). Call it \(r_3\).
Continue to divide the remainder from two steps prior by the remainder from the last step, until...
The remainder \(r_n\) is divisible by \(r_{n+1}\). The Euclidean algorithm stops now and \(r_{n+1}\) is \(\gcd(a,b)\).
Show that there is indeed some natural number \(n\) such that \(r_n\) is divisible by \(r_{n+1}\), so that the Euclidean algorithm must stop eventually. Furthermore, show that \(r_{n+1}\) is actually \(\gcd(a,b)\) (otherwise it is all in vain!).
Cut a deck of \(4\) cards. Are any of the cards in the same place as they were before?
We have a deck of \(13\) cards from Ace to King. Let Ace be the first card, \(2\) the second card and so on with King being the thirteenth card. How can you swap \(4\) and \(7\) (and leave all other cards where they are) by only switching adjacent pairs of cards?