Problems

Donald’s sister Maggie goes to a nursery. One day the teacher at the nursery asked Maggie and the other children to stand a circle. When Maggie came home she told Donald that it was very funny that in the circle every child held hands with either two girls or two boys. Given that there were five boys standing in the circle, how many girls were standing in the circle?

The king possesses \(7\) bags of gold coins, each containing \(100\) coins. While the coins in each bag appear identical, they vary in weight and they cannot be told apart by looking. The king recalls that within these bags, one contains coins that weigh \(7\)g each, another has coins weighing \(8\)g, the third bag contains coins weighing \(9\)g, the fourth has coins weighing \(10\)g, the fifth contains coins weighing \(11\)g, the sixth holds coins weighing \(12\)g, and finally, the seventh bag contains coins weighing \(13\)g each. However, he cannot remember which bag corresponds to which coin weight.
The king reported his situation to his chancellor, pointing to one of the bags, and asked how to determine the weight of the coins in that bag. The chancellor has large two-cup scales without weights. These scales can precisely indicate whether the weights on the cups are equal or, if not, which cup is heavier. Can the chancellor ascertain which coins are in the bag indicated by the king, using no more than two weightings? The chancellor is permitted to take as many coins as necessary to conduct the weightings.

Abigail’s little brother Carson found a big rectangular cake in the fridge and cut a small rectangular piece out of it.

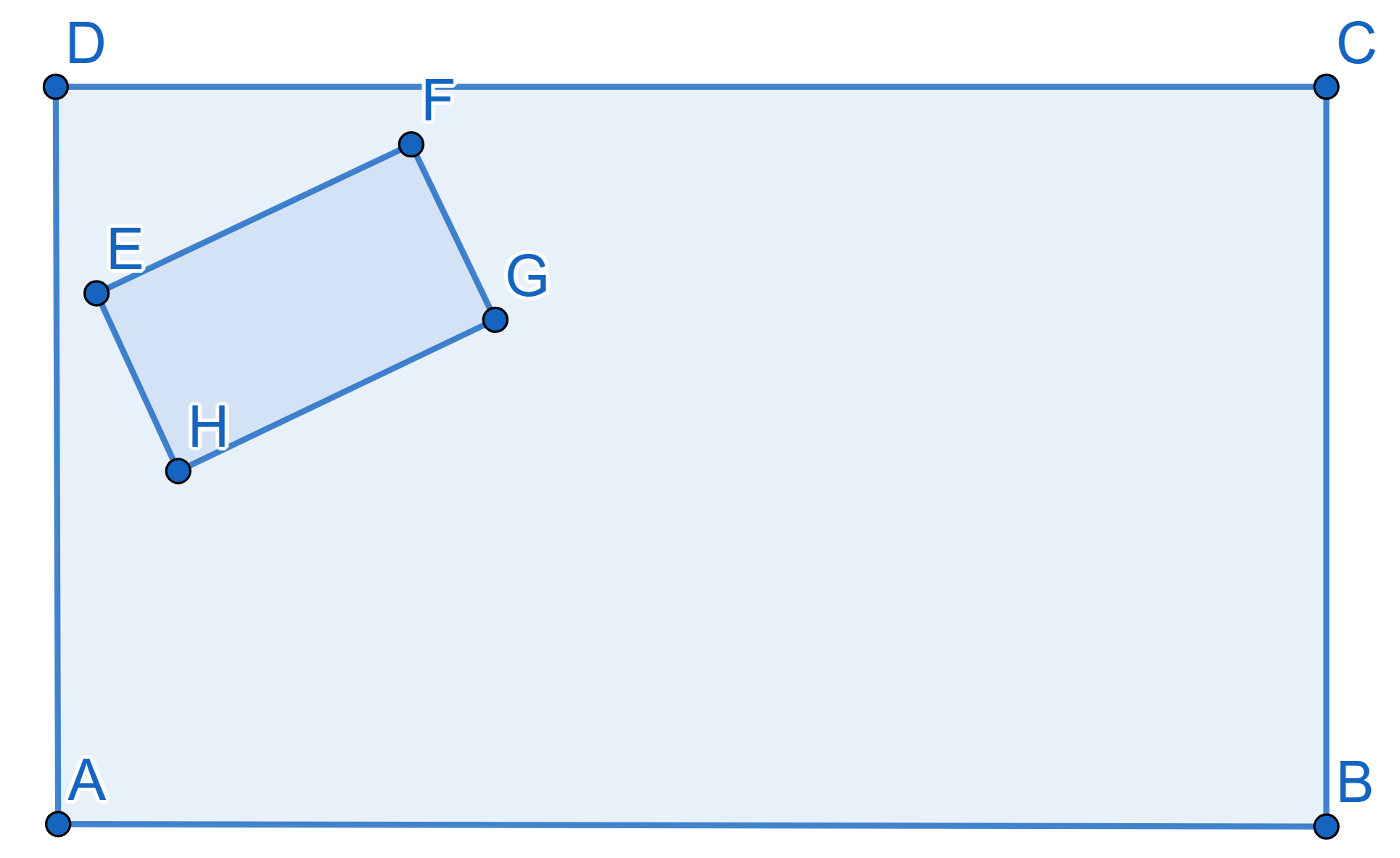
Now Abigail needs to find a way to cut the remaining cake into two pieces of equal area with only one straight cut. How could she do that? The removed piece can be of any size or orientation.

A chord of a circle is a straight line between two points on the circumference of the circle. Is it possible to draw five chords on a circle in such a way that there is a pentagon and two quadrilaterals among the parts into which these chords divide the circle?

There are \(20\) chairs in the room, which come in two colors: blue and red. Each chair is occupied by either a knight or a liar. Knights always tell the truth, while liars always lie. Initially, each of those seated claimed to be sitting on a blue chair. Then, they switched seats, after which half of the participants asserted that they were now sitting on blue chairs, while the other half claimed to be sitting on red ones. How many knights are currently occupying red chairs?

All the positive fractions smaller than \(1\) with denominators not more than \(100\) are written in a row. Isley and Ella put signs \("+"\) or \("-"\) in front of any fraction, which does not yet have a sign before it. They write signs in turns, but it is known that Isley has to make the last move and calculate the resulting sum. If the total sum turns out to be an integer number, then Ella will give her a chocolate bar. Will Isley be able to get a chocolate bar regardless of Ella’s actions?

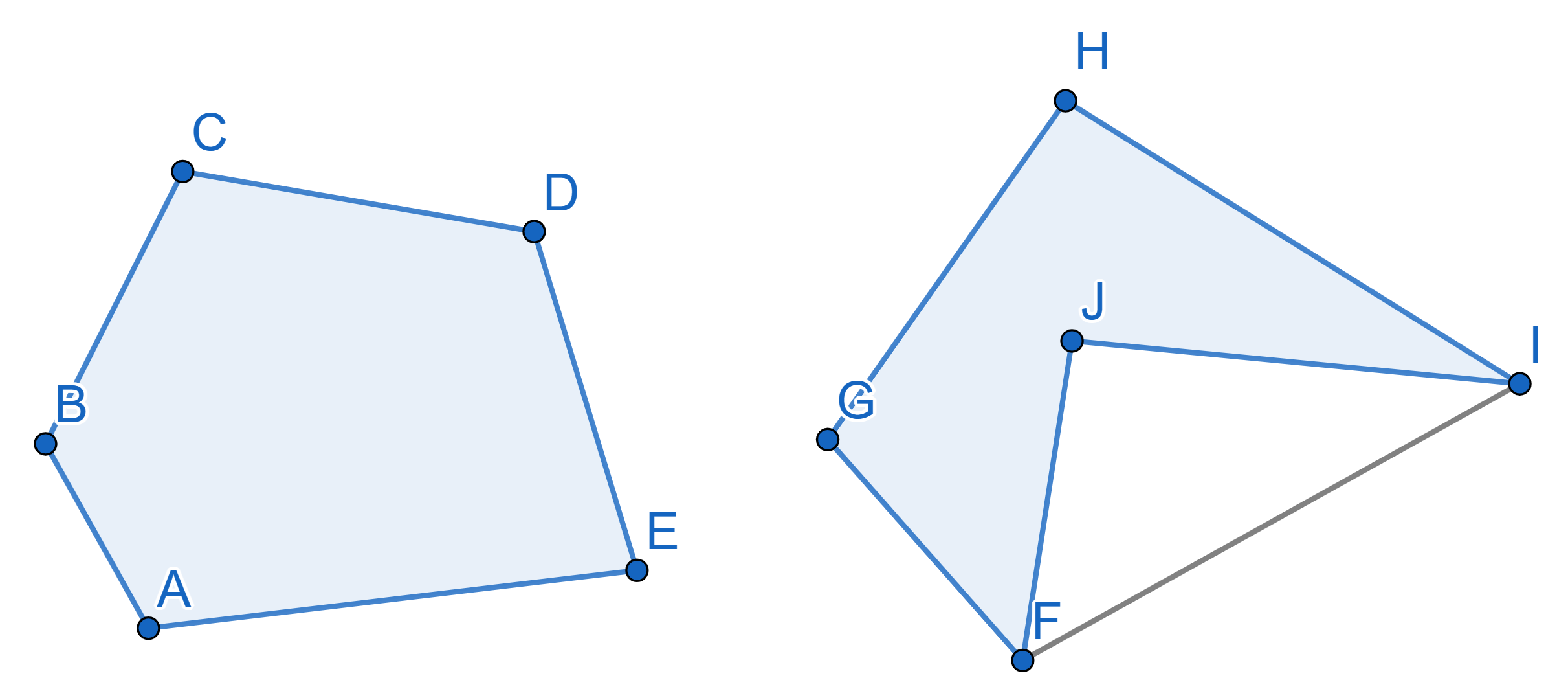
We say that a figure is convex if a segment connecting any two points lays fully within the figure. On the picture below the pentagon on the left is convex and the one on the right is not.

Is it possible to draw \(18\) points inside a convex pentagon so that each of the ten triangles formed by its sides and diagonals contains equal amount of points?

Cambria was building various cuboids from \(1\times 1\times1\) cubes. She initially built one cuboid, then increased its length and width by \(1\) and reduced its height by \(2\). She then understood that she needs the same number of \(1\times 1\times 1\) cubes to build both the original and new cuboids. Prove that the number of cubes used for each of the cuboids is divisible by \(3\).

Is it possible to cut an equilateral triangle into three equal hexagons?

A labyrinth was drawn on a \(5\times 5\) grid square with an outer wall and an exit one cell wide, as well as with inner walls running along the grid lines. In the picture, we have hidden all the inner walls from you (We give you several copies to facilitate drawing)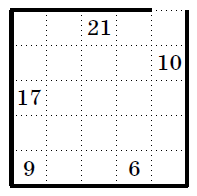 
Please draw how the walls were arranged. Keep in mind that the numbers in the cells represent the smallest number of steps needed to exit the maze, starting from that cell. A step can be taken to any adjacent cell vertically or horizontally, but not diagonally (and only if there is no wall between them, of course).