Problems
An ice cream machine distributes ice cream randomly. There are 5 flavours in the machine and you would like to have one of the available flavours at least 3 times, although you don’t mind which flavour it is. How many samples do you need to obtain in total to ensure that?
Prove that among \(11\) different infinite decimal fractions, you can choose two fractions which coincide in an infinite number of digits.
A convex polygon on the plane contains at least \(m^2+1\) points with integer coordinates. Prove that it contains \(m+1\) points with integers coordinates that lie on the same line.
Suppose a football team scores at least one goal in each of the \(20\) consecutive games. If it scores a total of \(30\) goals in those \(20\) games, prove that in some sequence of consecutive games it scores exactly \(9\) goals total.
The prime factorization of the number \(b\) is \(2 \times 5^2 \times 7 \times 13^2 \times 17\). The prime factorization of the number \(c\) is \(2^2 \times 5 \times 7^2 \times 13\). Is the first number divisible by the second one? Is the product of these two numbers, \(b \times c\), divisible by \(49000\)?
Find all the prime numbers \(p\) such that there exist natural numbers \(x\) and \(y\) for which \(p^x = y^3 + 1\).
Determine all prime numbers \(p\) such that \(5p+1\) is also prime.
Find all natural numbers \(n\) for which there exist integers \(a,b,c\) such that \(a+b+c = 0\) and the number \(a^n + b^n + c^n\) is prime.
Find all the prime numbers \(p\) such that the number \(2p^2+1\) is also prime.
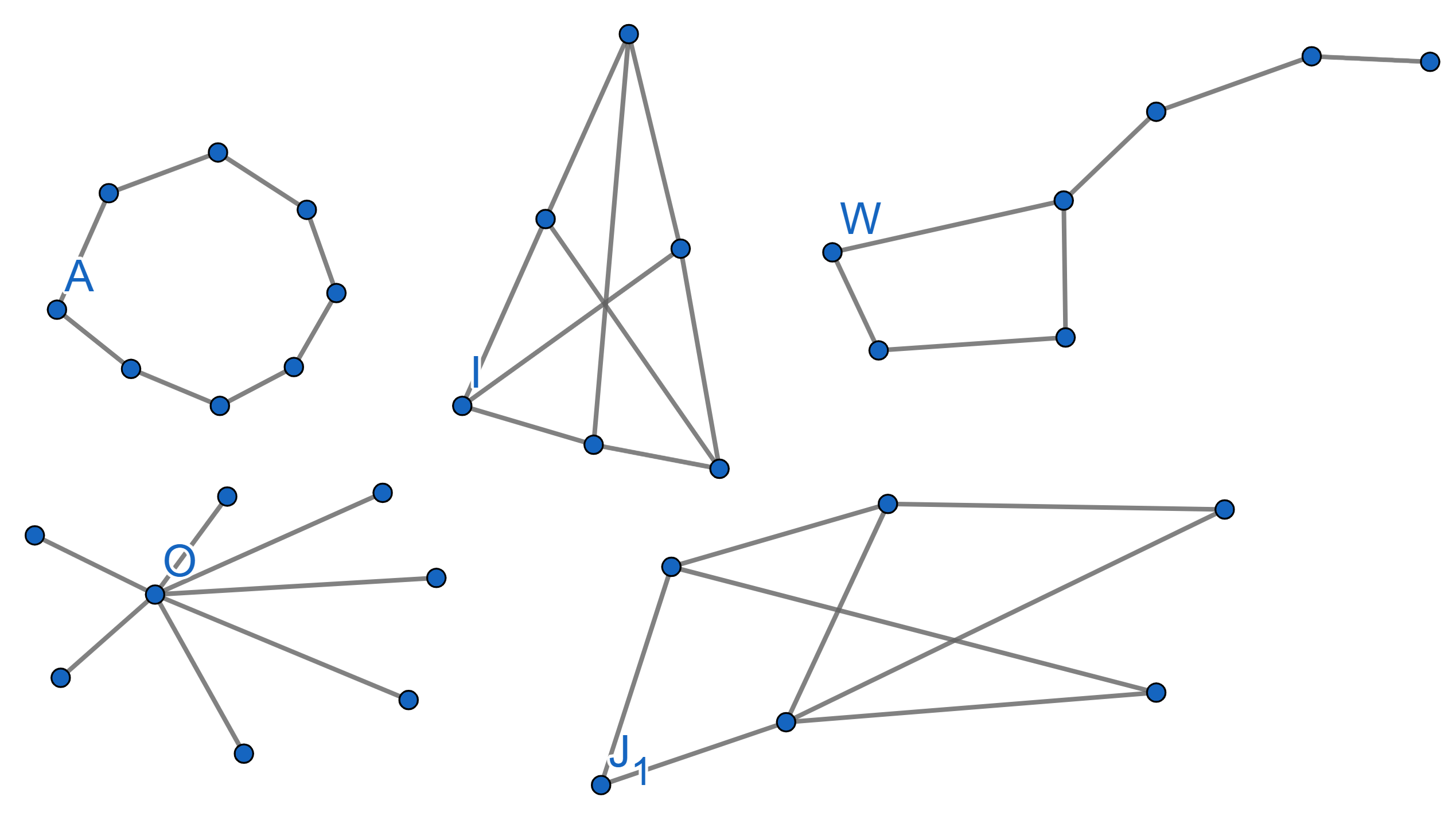
A graph is called Bipartite if it is possible to split all its vertices into two groups in such a way that there are no edges connecting vertices from the same group. Find out whic of the following graphs are bipartite and which are not: