Problems

Replace all stars with ”+” or ”$\times$” signs so the equation holds: $$1\ast 2\ast 3\ast 4\ast 5\ast 6=100$$ Extra brackets may be added if necessary. Please write down the expression into the answer box.

In how many ways can one change $\text{pounds}2$ into coins worth $50$p, $20$p and $10$p? One does not necessarily need to use all available coin types, i.e. having $5$ coins of $20$p and $10$ coins of $10$p is allowed.

In a lot of geometric problems the main idea is to find congruent figures. We call two polygons congruent if all their corresponding sides and angles are equal. Triangles are the easiest sort of polygons to deal with. Assume we are given two triangles $ABC$ and $A_1{B}_1{C}_1$ and we need to check whether they are congruent or not, some rules that help are:

• If all three corresponding sides of the triangles are equal, then the triangles are congruent.

• If, in the given triangles $ABC$ and $A_1{B}_1{C}_1$, two corresponding sides $AB=A_1{B}_1$, $AC=A_1{C}_1$ and the angles between them $\mathrm{\angle }BAC=\mathrm{\angle }{B}_1{A}_1{C}_1$ are equal, then the triangles are congruent.

• If the sides $AB=A_1{B}_1$ and pairs of the corresponding angles next to them $\mathrm{\angle }CAB=\mathrm{\angle }{C}_1{A}_1{B}_1$ and $\mathrm{\angle }CBA=\mathrm{\angle }{C}_1{B}_1{A}_1$ are equal, then the triangles are congruent.

At a previous geometry lesson we have derived these rules from the axioms of Euclidean geometry, so now we can just use them.

Consider two congruent triangles $ABC$ and $A_1{B}_1{C}_1$. We draw a point $M$ on the side $BC$ and a point $M_1$ on the side $B_1{C}_1$ such that the ratio of lengths $BM:MC$ is equal to the ratio of lengths $B_1{M}_1:M_1{C}_1$. Prove that $AM=A_1{M}_1$.

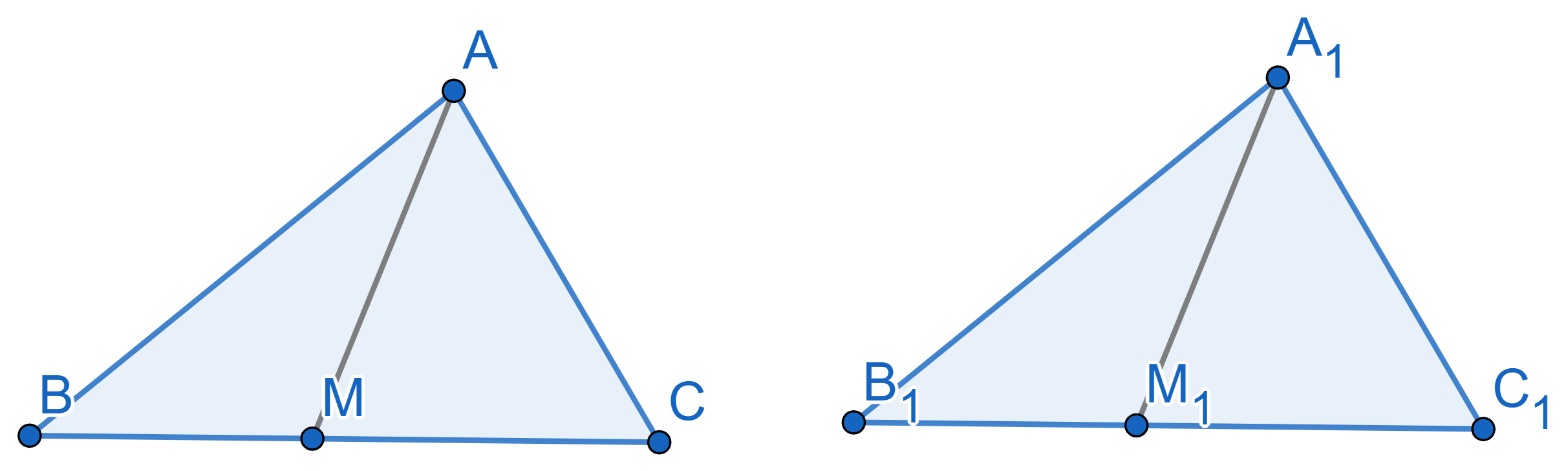
We call a median the segment from the vertex of a triangle to the midpoint of the opposite side. Prove that in two congruent triangles, the corresponding medians are of equal length.

We call a bisector the segment from the vertex of a triangle to the opposite side which divides in half the angle next to the starting vertex. Prove that in two congruent triangles, the corresponding bisectors are of equal length.

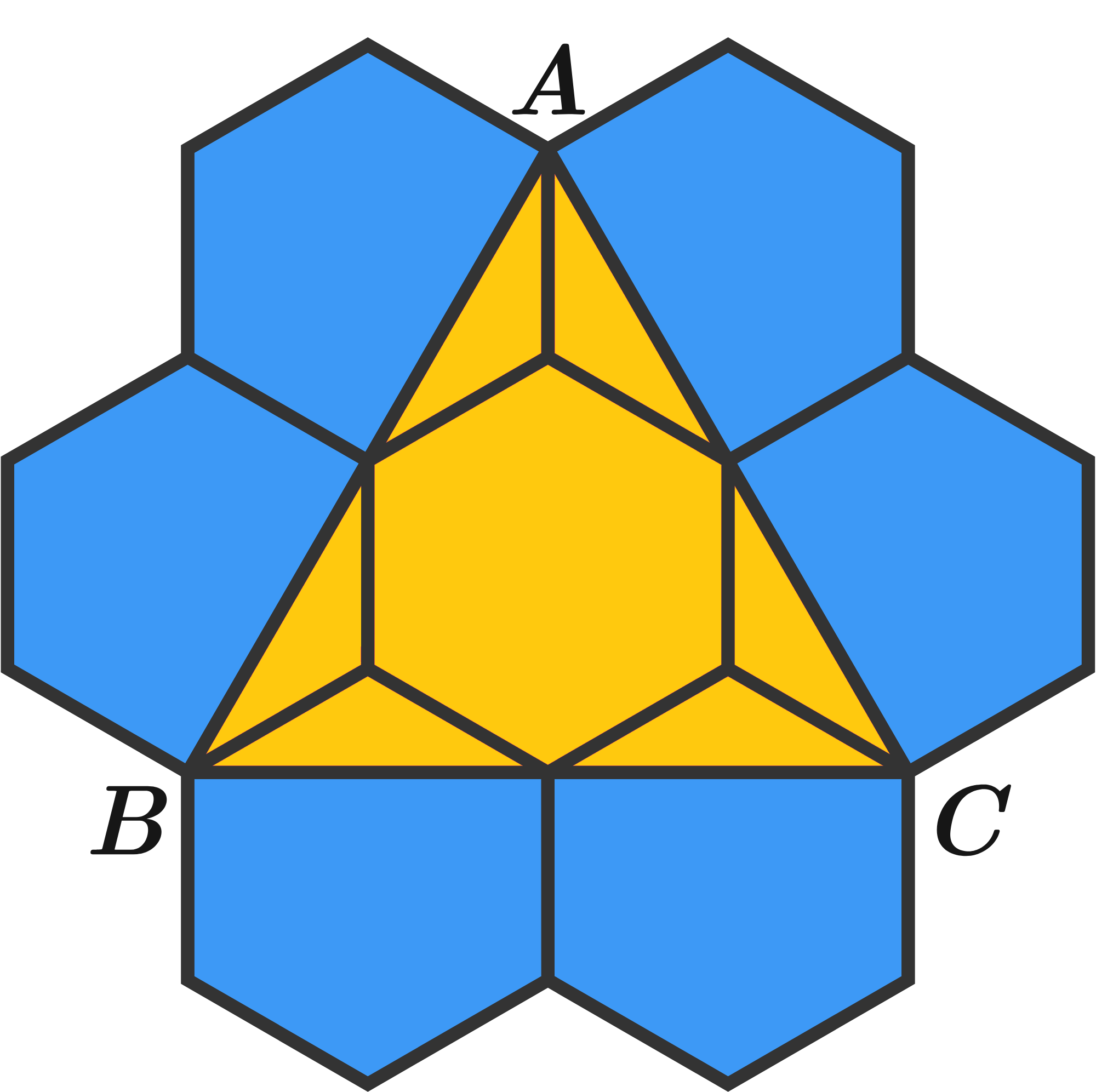
$7$ identical hexagons are arranged in a pattern on the picture below. Each hexagon has an area of $8$. What is the area of the triangle $\mathrm{△}ABC$?

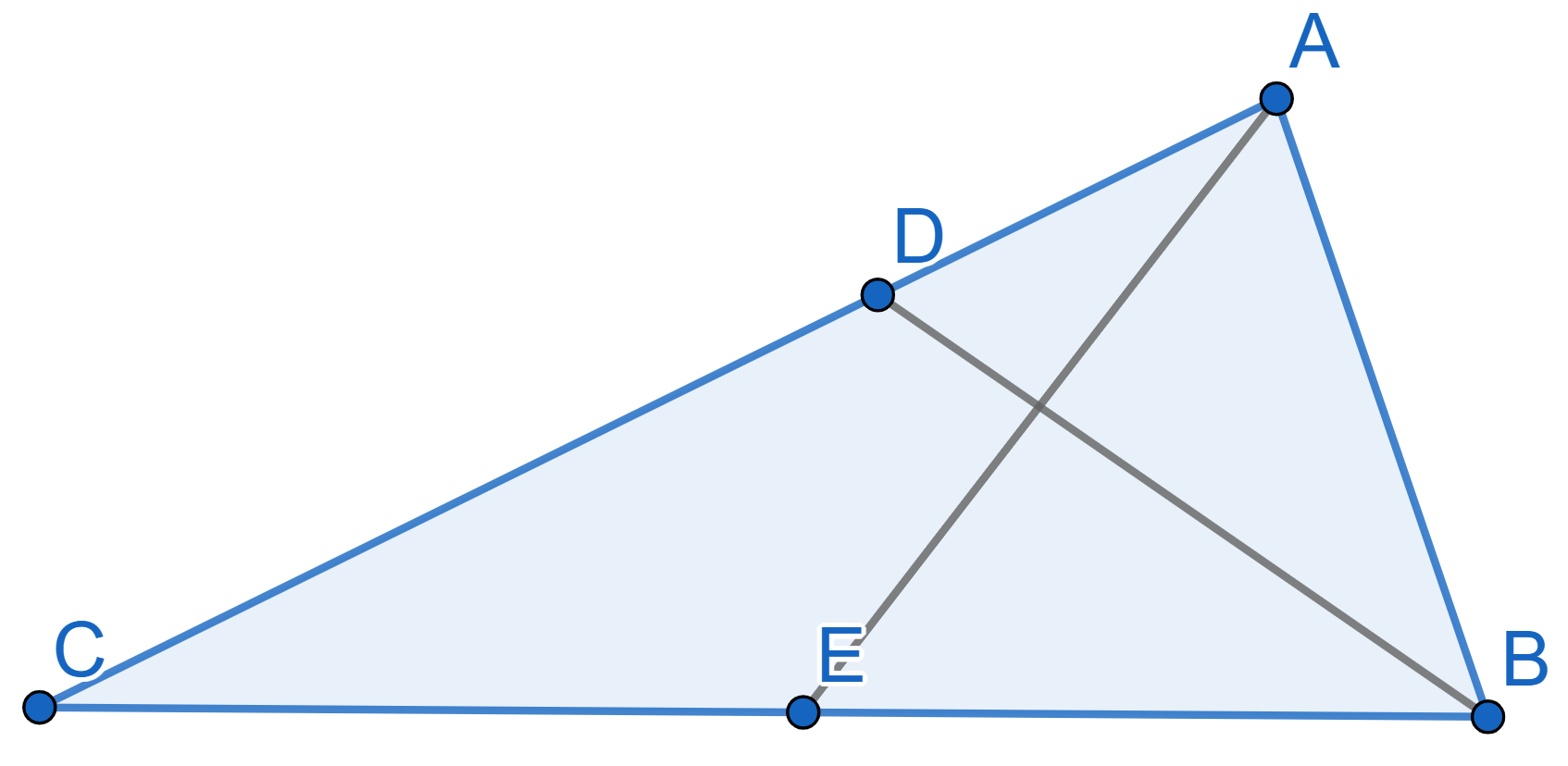
In the triangle $ABC$ the bisector $BD$ coincides with the height. Prove that $AB=BC$.

In the triangle $ABC$ the median $BD$ coincides with the height. Prove that $AB=BC$.

In the triangle $ABC$ with $BC=12$, the median $AE$ is perpendicular to the bisector $BD$. Find the length of $AB$.