Problems

Let \(ABCD\) be a square, a point \(I\) a random point on the plane. Consider the four points, symmetric to \(I\) with respect to the midpoints of \(AB, BC, CD, AD\). Prove that these new four points are vertices of a square.

Replace the stars with positive whole numbers so that \[\frac{1}{*}+\frac{1}{*}=\frac{7}{48}.\]

Let \(ABCD\) be a quadrilateral with the point \(E\) of intersection of diagonals. Consider the triangles \(ABE\), \(BCE\), \(CDE\), \(ADE\) and their correspondent points of intersection of medians \(K,J,M,L\).

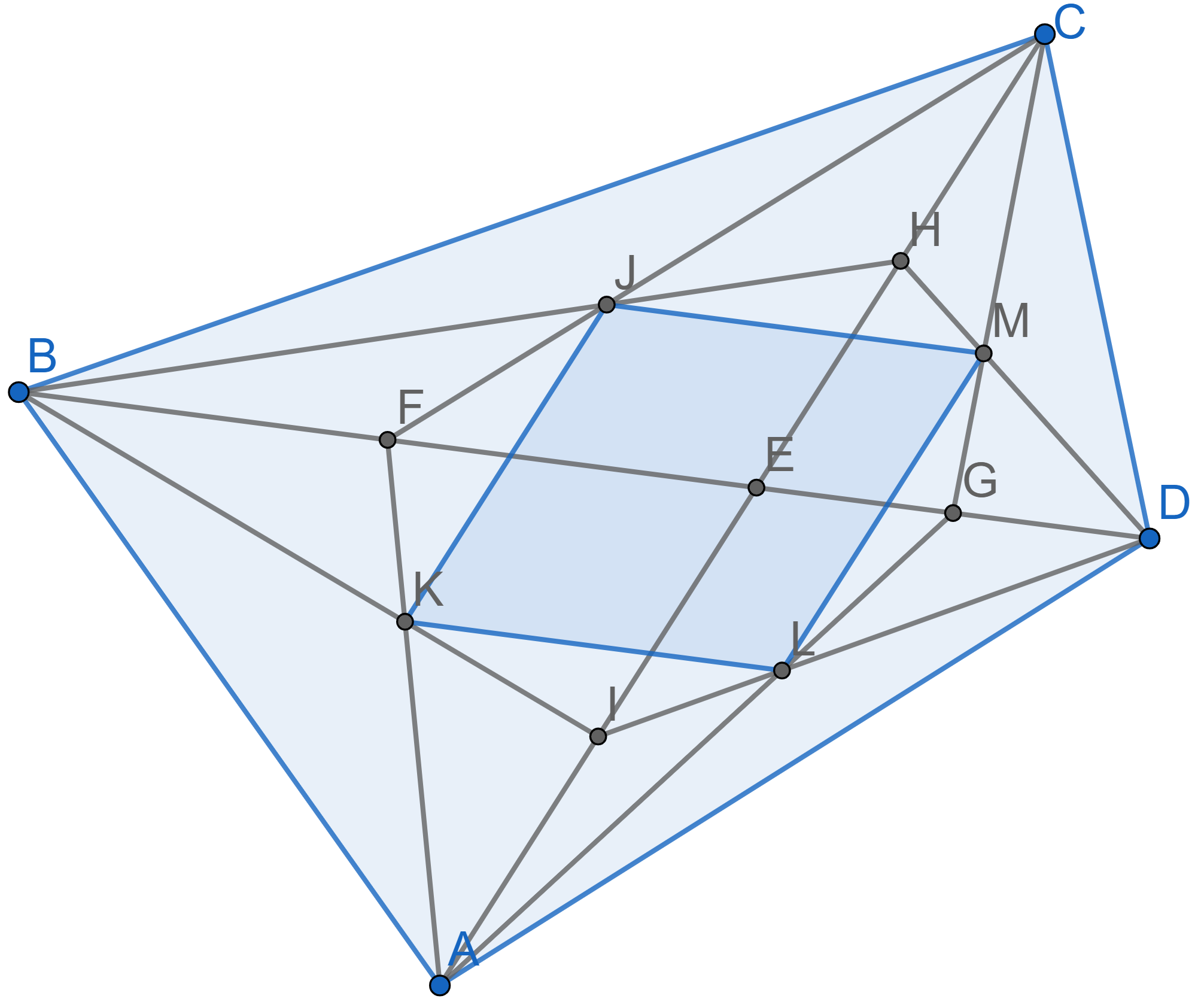
Prove that \(KJML\) is a parallelogram.