Problems
Prove the magic trick for the number \(1089
= 33^2\): if you take any \(3\)-digit number \(\overline{abc}\) with digits coming in
strictly descending order and subtract from it the number obtained by
reversing the digits of the original number \(\overline{abc} - \overline{cba}\) you get
another \(3\)-digit number, call it
\(\overline{xyz}\). Then, no matter
which number you started with, the sum \(\overline{xyz} + \overline{zyx} =
1089\).
Recall that a number \(\overline{abc}\)
is divisible by \(11\) if and only if
\(a-b+c\) also is.
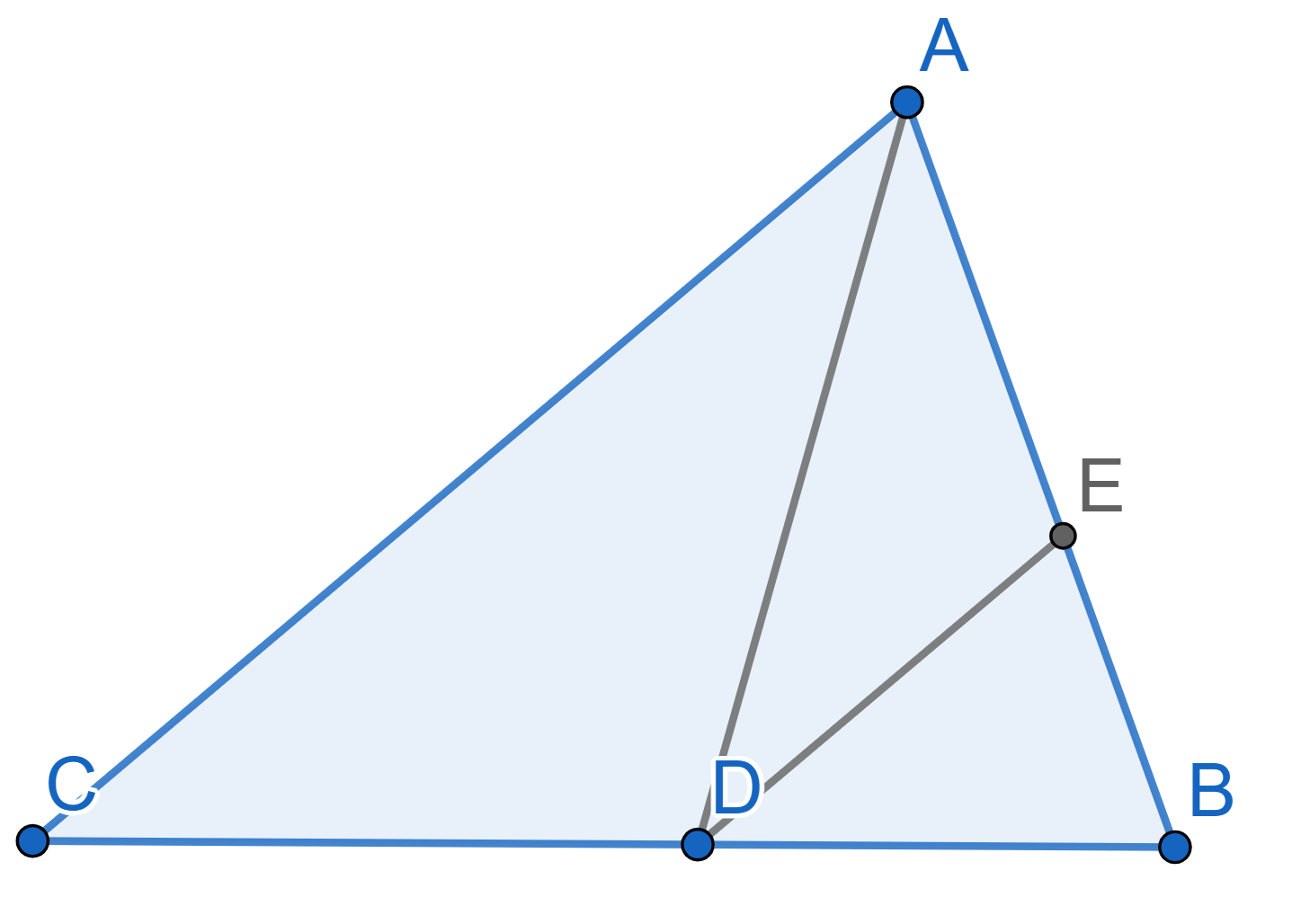
On the diagram below \(AD\) is the
bisector of the triangle \(ABC\). The
point \(E\) lies on the side \(AB\), with \(AE =
ED\). Prove that the lines \(AC\) and \(DE\) are parallel.
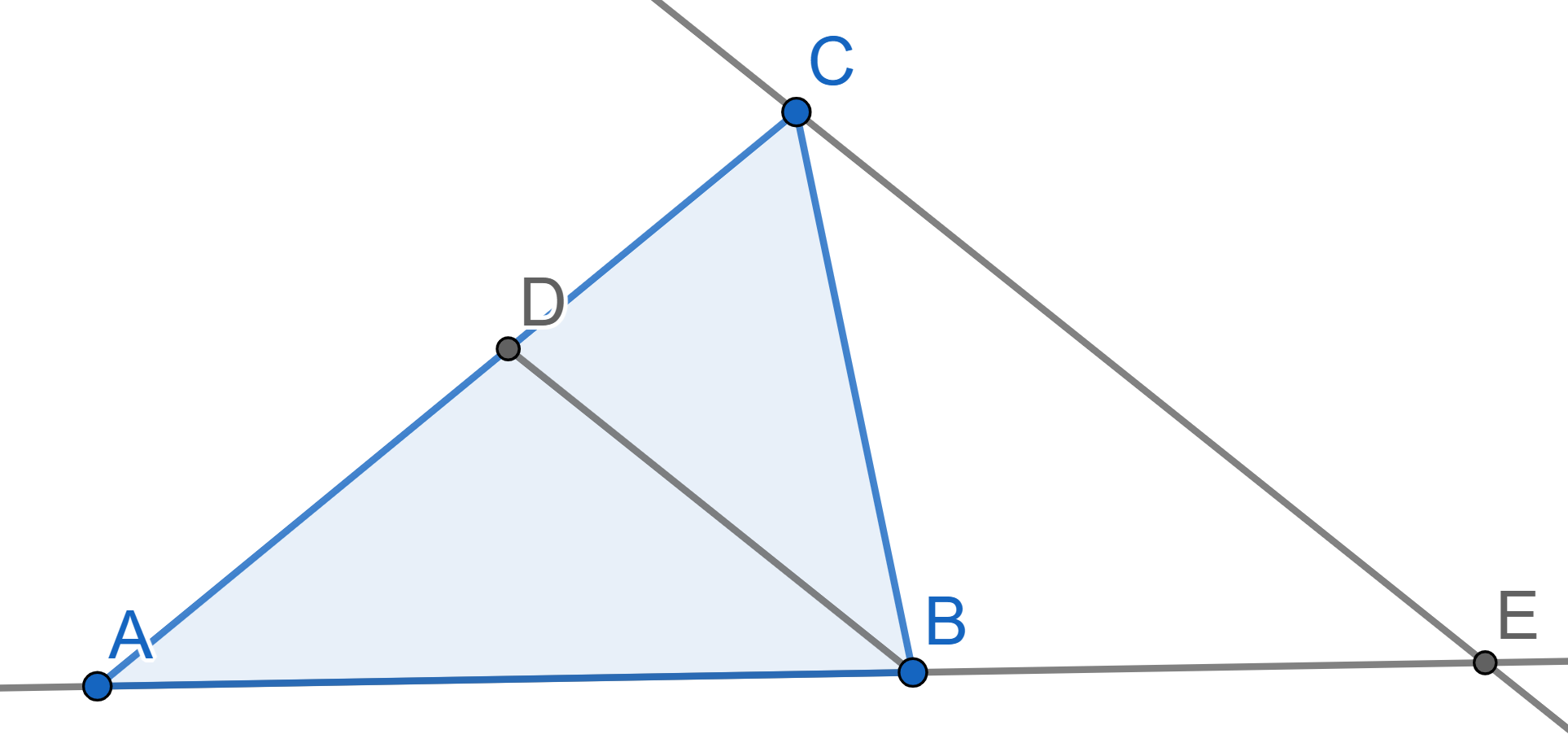
On the diagram below the line \(BD\)
is the bisector of the angle \(\angle
ABC\) in the triangle \(ABC\). A
line through the vertex \(C\) parallel
to the line \(BD\) intersects the
continuation of the side \(AB\) at the
point \(E\). Find the angles of the
triangle \(BCE\) triangle if \(\angle ABC = 110^{\circ}\).
We want to wrap \(12\) Christmas presents in different coloured paper. We have \(6\) different patterns of paper and we want to use each one exactly twice. In how many ways can we do this?
Mr Roberts wants to place his little stone sculptures of vegetables
on the different shelves around the house. He has \(17\) sculptures in total and three shelves
that can fit \(7\), \(8\) and \(2\) sculptures respectively. In how many
ways can he do this?
The order of sculptures on the shelf does not matter.
In a certain state, there are three types of citizens:
A fool considers everyone a fool and themselves smart;
A modest clever person knows truth about everyone’s intellectual abilities and consider themselves a fool;
A confident clever person knows about everyone intellectual abilities correctly and consider themselves smart.
There are \(200\) deputies in the High Government. The Prime Minister conducted an anonymous survey of High Government members, asking how many smart people are there in the High Government. After reading everyone’s response he could not find out the number of smart people. But then the only member who did not participate in the survey returned from the trip. They filled out a questionnaire about the entire Government including themselves and after reading it the Prime Minister understood everything. How many smart could there be in the High Government (including the traveller)?
The dragon locked six dwarves in the cave and said, "I have seven caps of the seven colors of the rainbow. Tomorrow morning I will blindfold you and put a cap on each of you, and hide one cap. Then I’ll take off the blindfolds, and you can see the caps on the heads of others, but not your own and I won’t let you talk any more. After that, everyone will secretly tell me the color of the hidden cap. If at least three of you guess right, I’ll let you all go. If less than three guess correctly, I’ll eat you all for lunch." How can dwarves agree in advance to act in order to be saved?
Do there exist two numbers such that their sum, quotient and product would be all equal to each other?
It is easy to construct one equilateral triangle using three identical matches. Is it possible to construct four equilateral triangles by adding just three more matches identical to the original ones?
Winnie the Pooh has five friends, each of whom has pots of honey in their house: Tigger has \(1\) pot, Piglet has \(2\), Owl has \(3\), Eeyore has \(4\), and Rabbit has \(5\). Winnie the Pooh comes to visit each friend in turn, eats one pot of honey and takes the other pots with him. He came into the last house carrying \(10\) pots of honey. Whose house could Pooh have visited last?