Problems
Let \(A\), \(B\), \(C\) and \(D\) be four points labelled clockwise on the circumference of a circle. The diagonals \(AC\) and \(BD\) intersect at the centre \(O\) of the circle. What can be deduced about the quadrilateral \(ABCD\)?
Consider the 7 different tetrominoes. Is it possible to cover a \(4\times7\) rectangle with exactly one copy of each of the tetrominoes? If it is possible, then provide an example layout. If it is not possible, then prove that it’s impossible.
We allow rotation of the tetrominoes, but not reflection. This means that we consider \(S\) and \(Z\) as different, as well as \(L\) and \(J\).
In the following grid, how many different ways are there of getting from the bottom left triangle to the bottom right triangle? You must only go from between triangles that share an edge and you can visit each triangle at most once. (You don’t have to visit all of the triangles.)
Let’s play some games today! We will play a classic game known as nim, which is thought to be one of the oldest games.
Typically people play nim using matchsticks, though stones and coins are popular too. There are a few heaps of matchsticks in nim. Players take turns to remove matchsticks from a heap of their choosing. The player can remove any number of matchsticks they wish from that heap. Whoever has no matchsticks left to take loses.
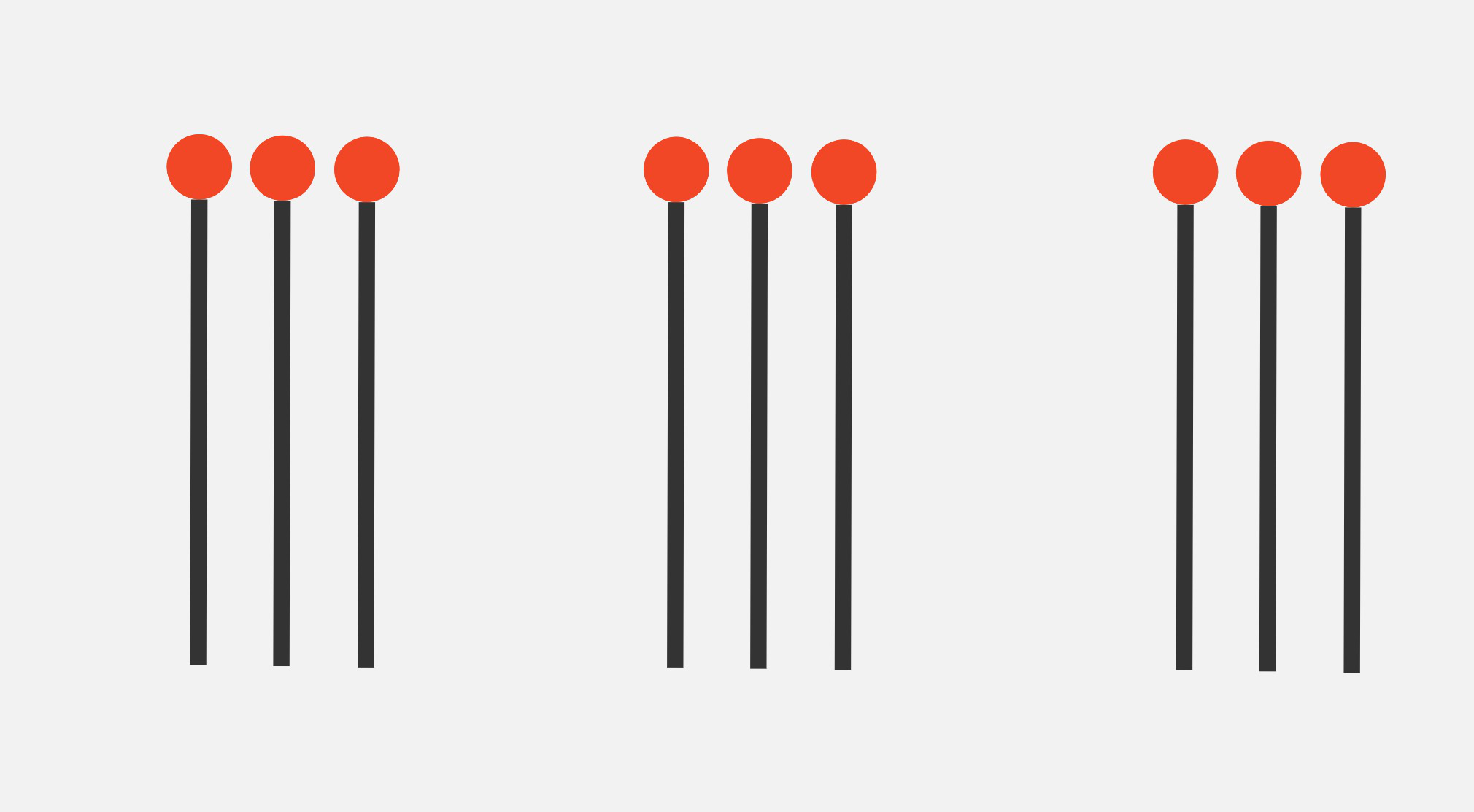
This following position will be written as \(\text{Nim}(3,3,3)\):
As another example, this is \(\text{Nim}(1,2,3,4)\):
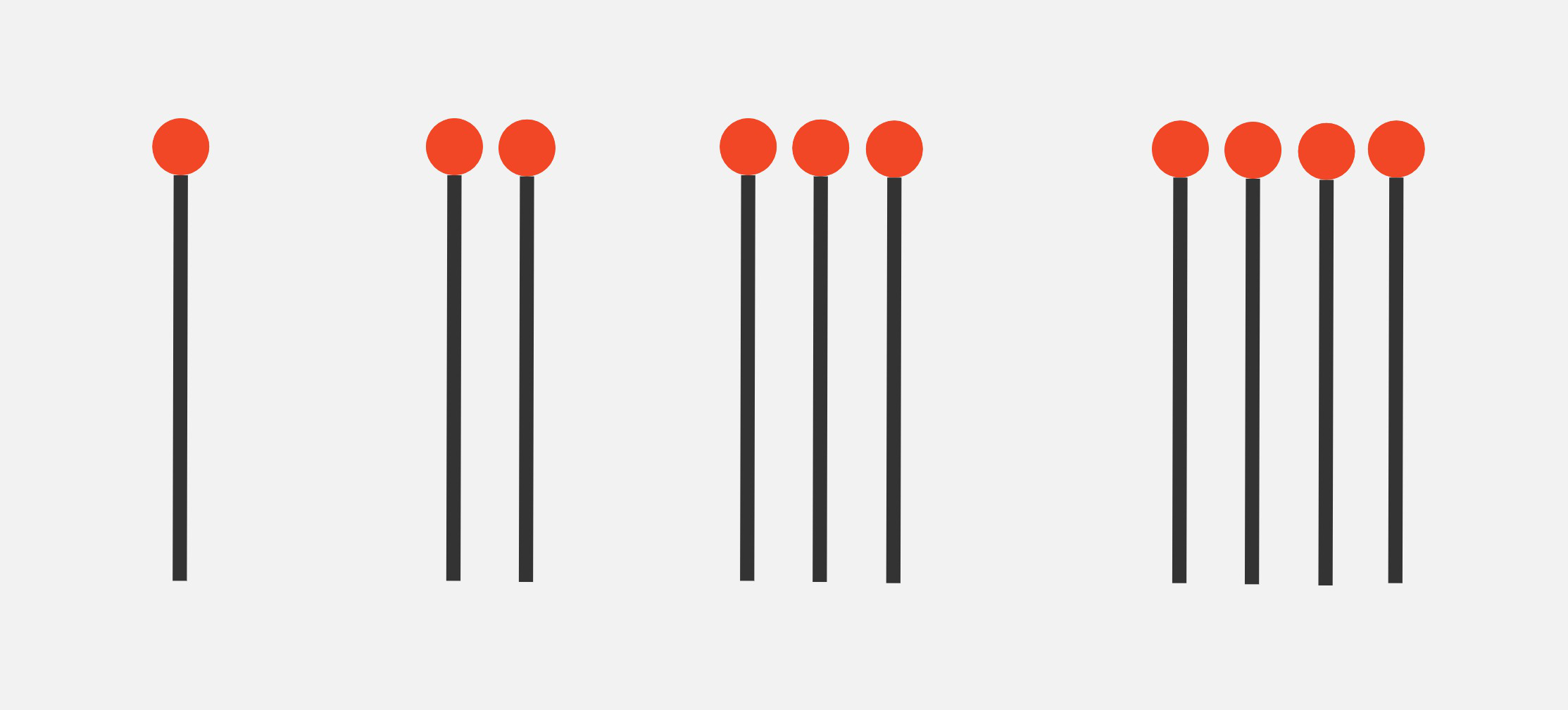
We will omit heaps of size zero, so \(\text{Nim}(3,0,3,0,3)\) is the same as \(\text{Nim}(3,3,3)\).
Nim is important because a large class of games are equivalent to it despite its simple appearance. The interested reader should look up “Sprague-Grundy Theorem".
Let us introduce a few terms that will be helpful for analyzing games. A game \(G\) consists of some positions and a set of rules. A position \(g\) in the game \(G\) is called a winning position if the player starting this turn has a winning strategy. This means as long as the player starting this turn continues to play optimally, the second player has to lose. Conversely, a position \(g\) is a losing position if the player starting this turn has no winning strategy.
Two fractions sum up to \(1\), but their difference is \(\frac1{10}\). What are they?
On her birthday, my grandma was asked how old she was. She said: "Start with the year I was born. Add the current year to it. Then, from the sum subtract the year I celebrated by \(20\)th birthday. From that, take away the year I was \(30\). The result will be \(16\)." How old is my grandma?
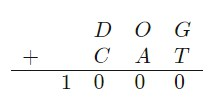
In the long addition above, each letter corresponds to a different digit. What is the sum \(D + O +G + C +A +T\)?
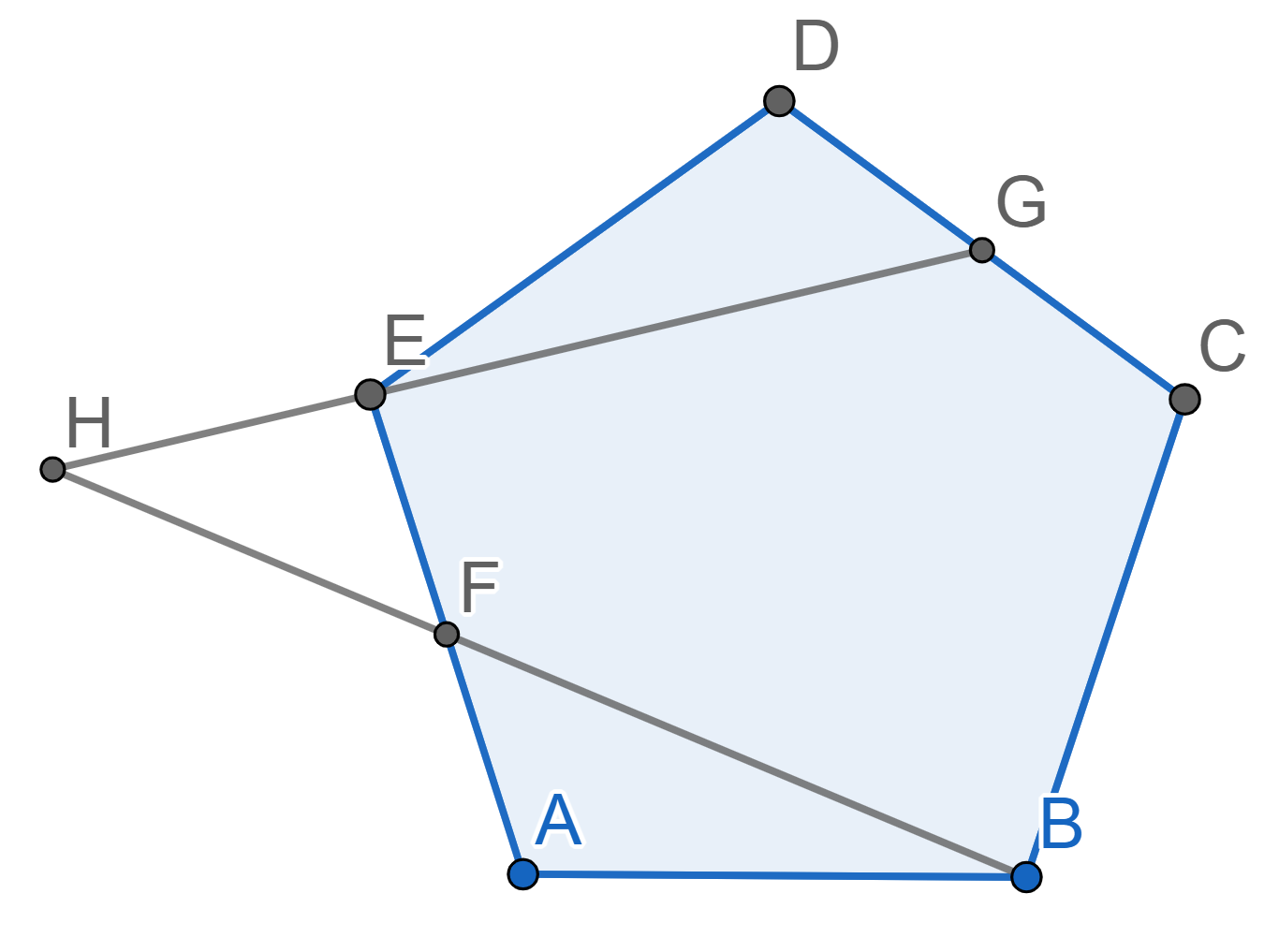
Let \(ABCDE\) be a regular pentagon. The point \(G\) is the midpoint of \(CD\), the point \(F\) is the midpoint of \(AE\). The lines \(EG\) and \(BF\) intersect at the point \(H\). Find the angle \(EHF\).
I have three positive integers. When you add them together, you get \(15\). When you multiply the three numbers together, you get \(120\).
What are the three numbers?
If a magician puts \(1\) dove into his hat, he pulls out \(2\) rabbits and \(2\) flowers from it. If the magician puts \(1\) rabbit in, he pulls out \(2\) flowers and \(2\) doves. If he puts \(1\) flower in, he pulls out \(1\) rabbit and \(3\) doves. The magician starts with \(1\) rabbit. Could he end up with the same number of rabbits, doves, and flowers after performing his hat trick several times?