Problems

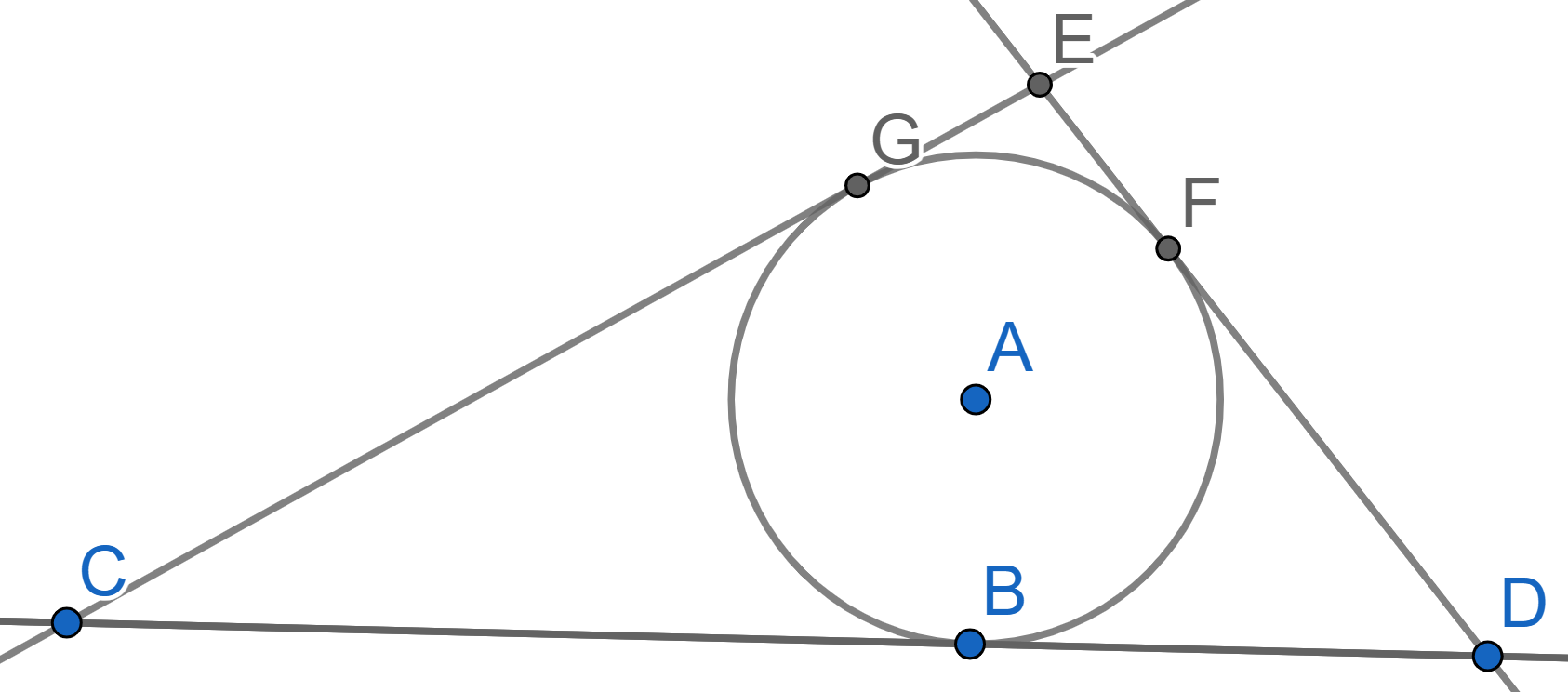
A circle with center \(A\) is inscribed into the triangle \(CDE\), so that all the sides of the triangle are tangent to the circle. We know the lengths of the segments \(ED=c, CD=a, EC=b\). The line \(CD\) is tangent to the circle at the point \(B\) - find the lengths of segments \(BD\) and \(BC\).

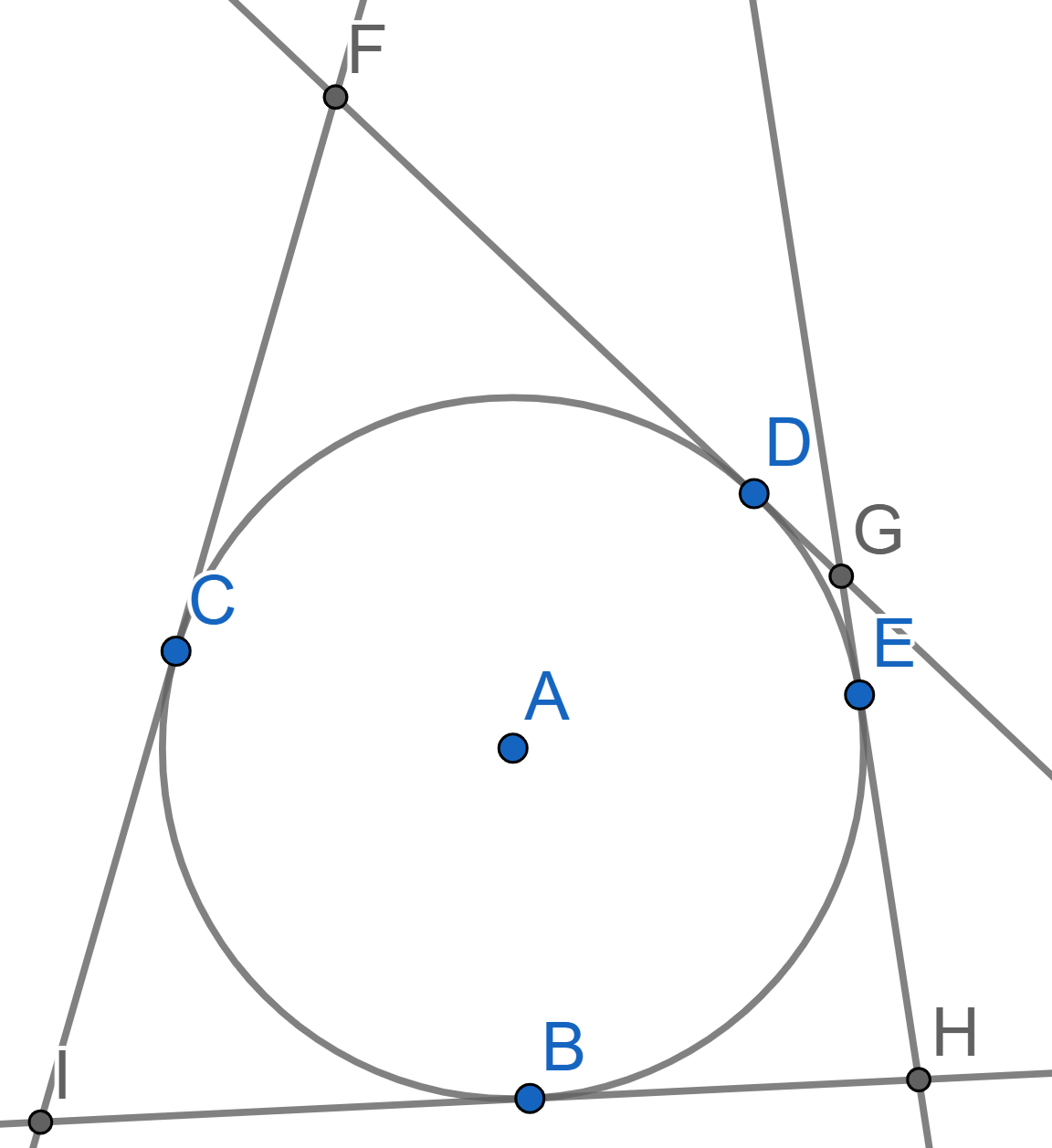
A circle with center \(A\) is tangent to all the sides of the quadrilateral \(FGHI\) at the points \(B,C,D,E\). Prove that \(FG+HI = GH+FI\).

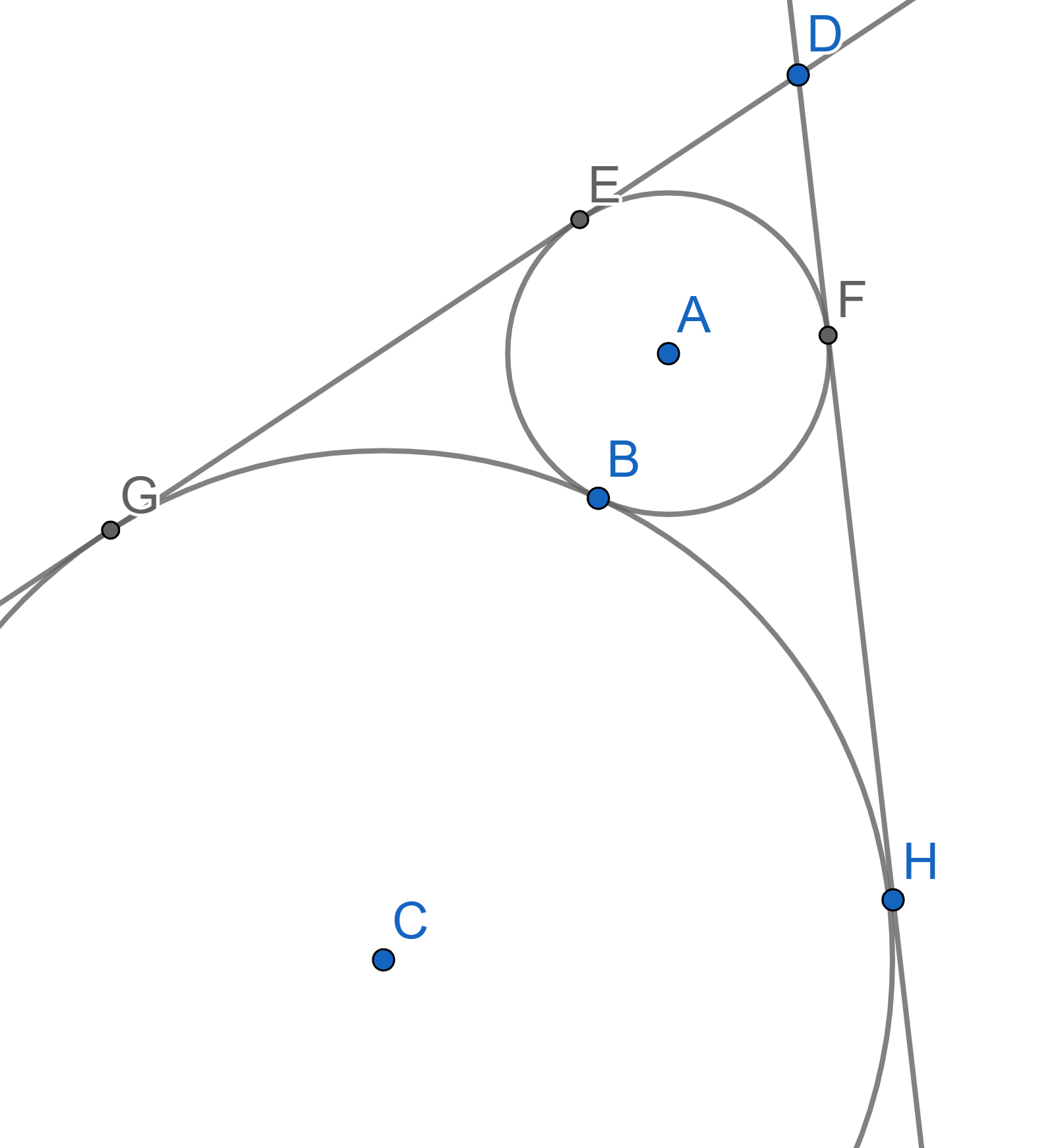
Two circles with centres \(A\) and \(C\) are tangent to each other at the point \(B\). Both circles are tangent to the sides of an angle with vertex \(D\). It is known that the angle \(\angle EDF = 60^{\circ}\) and the radius of the smaller circle \(AF=5\). Find the radius of the large circle.

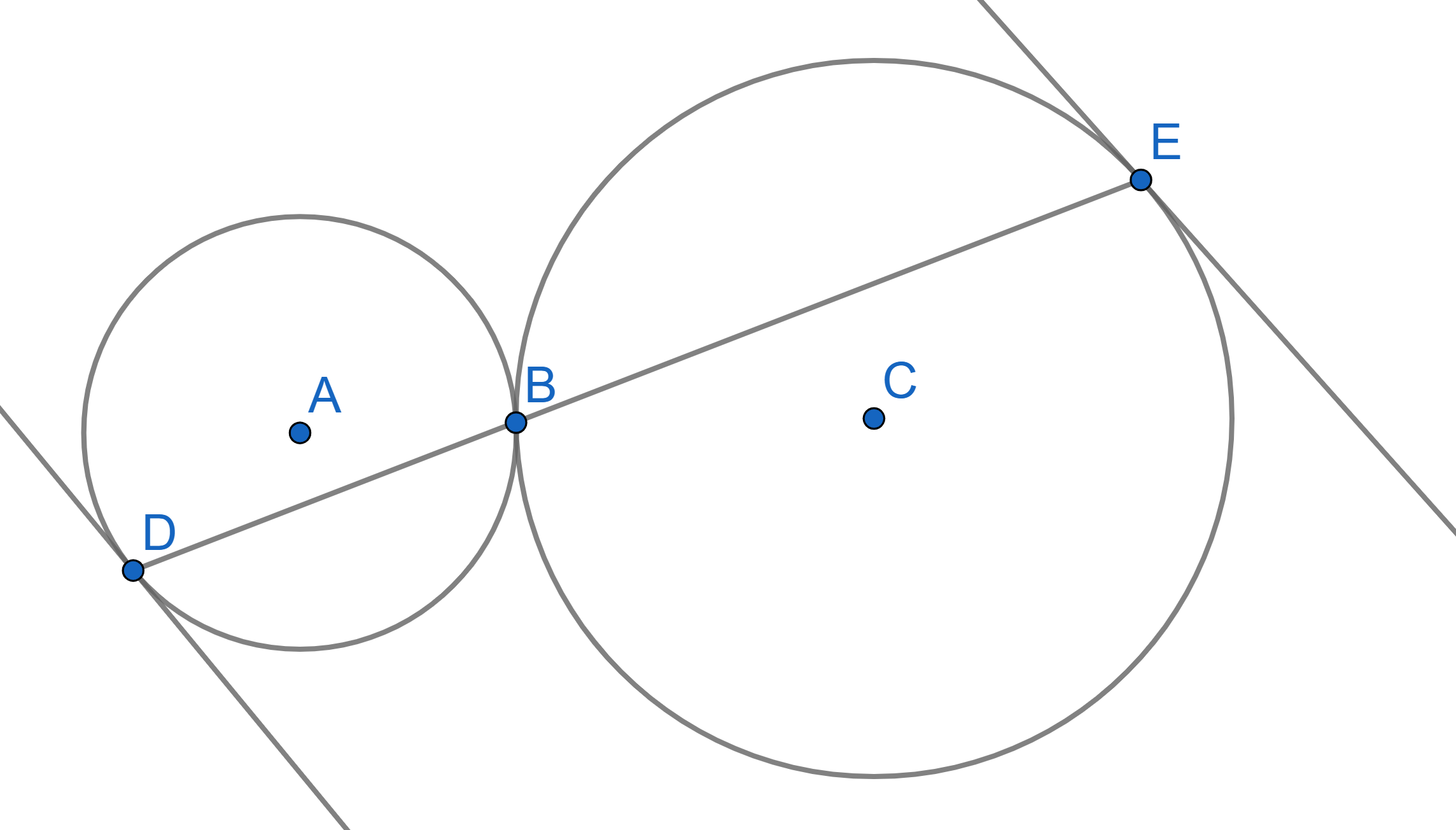
Two circles with centres \(A\) and \(C\) are tangent to each other at the point \(B\). Two points \(D\) and \(E\) are chosen on the circles in such a way that a segment \(DE\) passes through the point \(B\). Prove that the tangent line to one circle at the point \(D\) is parallel to the tangent line to the other circle at the point \(E\).

Geometry reminder

We call two polygons congruent if all their corresponding sides and angles are equal. Triangles are the easiest sort of polygons to deal with. Assume we are given two triangles \(ABC\) and \(A_1B_1C_1\) and we need to check whether they are congruent or not, some rules that help are:

• If all three corresponding sides of the triangles are equal, then the triangles are congruent.

• If, in the given triangles \(ABC\) and \(A_1B_1C_1\), two corresponding sides \(AB=A_1B_1\), \(AC=A_1C_1\) and the angles between them \(\angle BAC = \angle B_1A_1C_1\) are equal, then the triangles are congruent.

• If the sides \(AB=A_1B_1\) and pairs of the corresponding angles next to them \(\angle CAB = \angle C_1A_1B_1\) and \(\angle CBA = \angle C_1B_1A_1\) are equal, then the triangles are congruent.

The basic principles about parallel lines and general triangles are:
1. The supplementary angles (angles "hugging" a straight line) add up to \(180^{\circ}\).
2. The sum of all internal angles of a triangle is also \(180^{\circ}\).
3. A line cutting two parallel lines cuts them at the same angles (these are called corresponding angles).
4. In an isosceles triangle (which has two sides of equal lengths), two angles touching the third side are equal.

Is it true that if \(a\) is a positive number, then \(a^2 \ge a\)? What about \(a^2 +1 \ge a\)?

Show for positive \(a\) and \(b\) that \(a^2 +b^2 \ge 2ab\).

Is it true that if \(b\) is a positive number, then \(b^3 + b^2 \ge b\)? What about \(b^3 +1 \ge b\)?

Show that if \(a\) is positive, then \(1+a \ge 2 \sqrt{a}\).

Let \(k\) be a natural number, prove the following inequality. \[\frac1{k^2} > \frac1{k} - \frac1{k+1}.\]