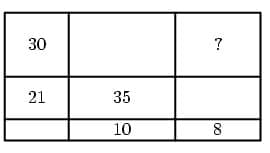
Problems
Each number denotes the area of the rectangle it is written into. What number should be written where the "?" character is?
A square was cut with two parallel lines. The perpendicular distance between these two lines is \(6\)cm. One of them goes through the top right corner and the other through the bottom left corner. The three regions obtained this way, two triangles and a parallelogram, have equal areas. What is the area of the square?

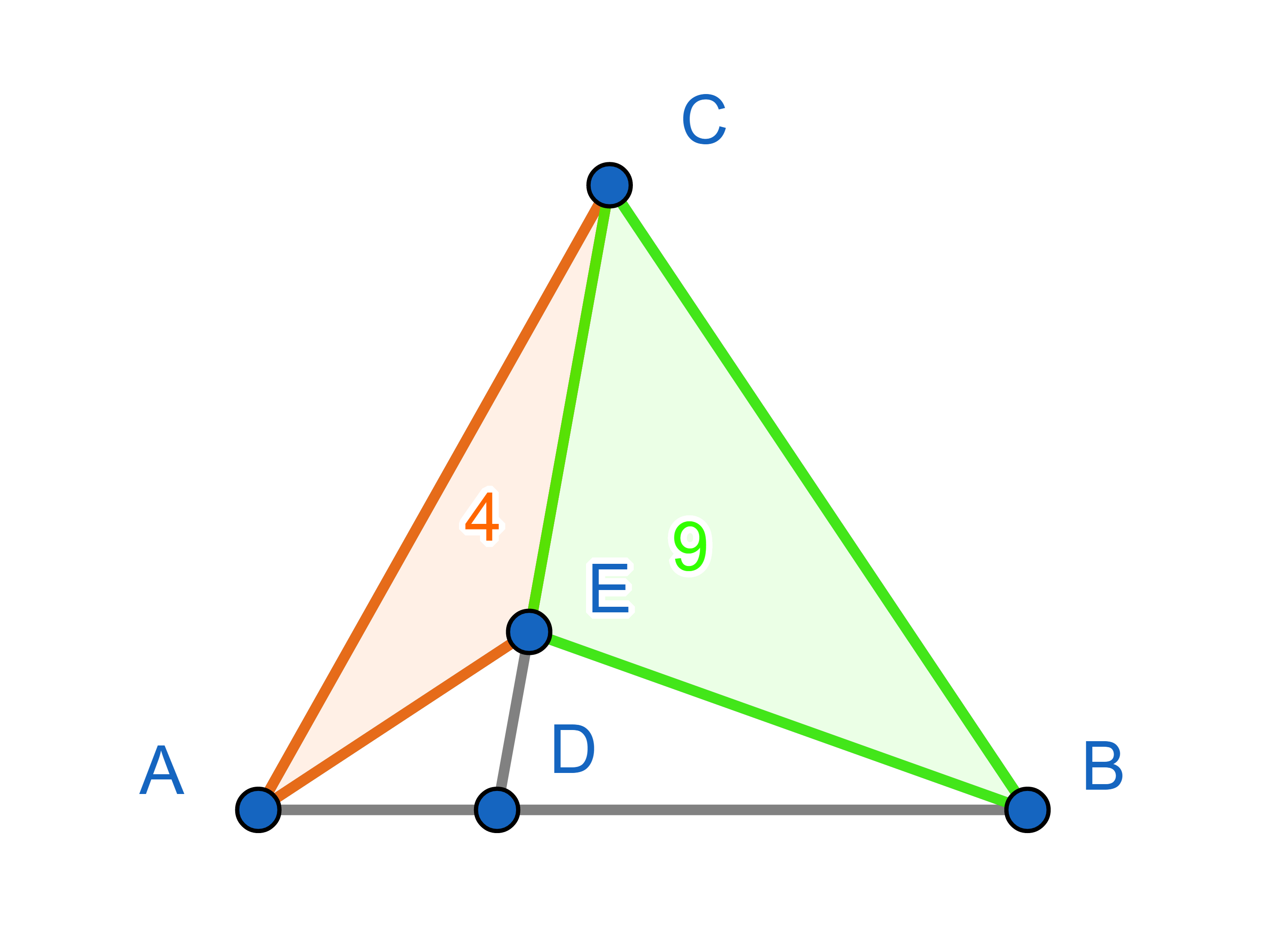
The area of the triangle \(\triangle AEC\) is \(4\), the area of the triangle \(\triangle BCE\) is \(9\) and the area of the triangle \(\triangle ABC\) is \(21\). What is the area of the triangle \(\triangle ADE\)?
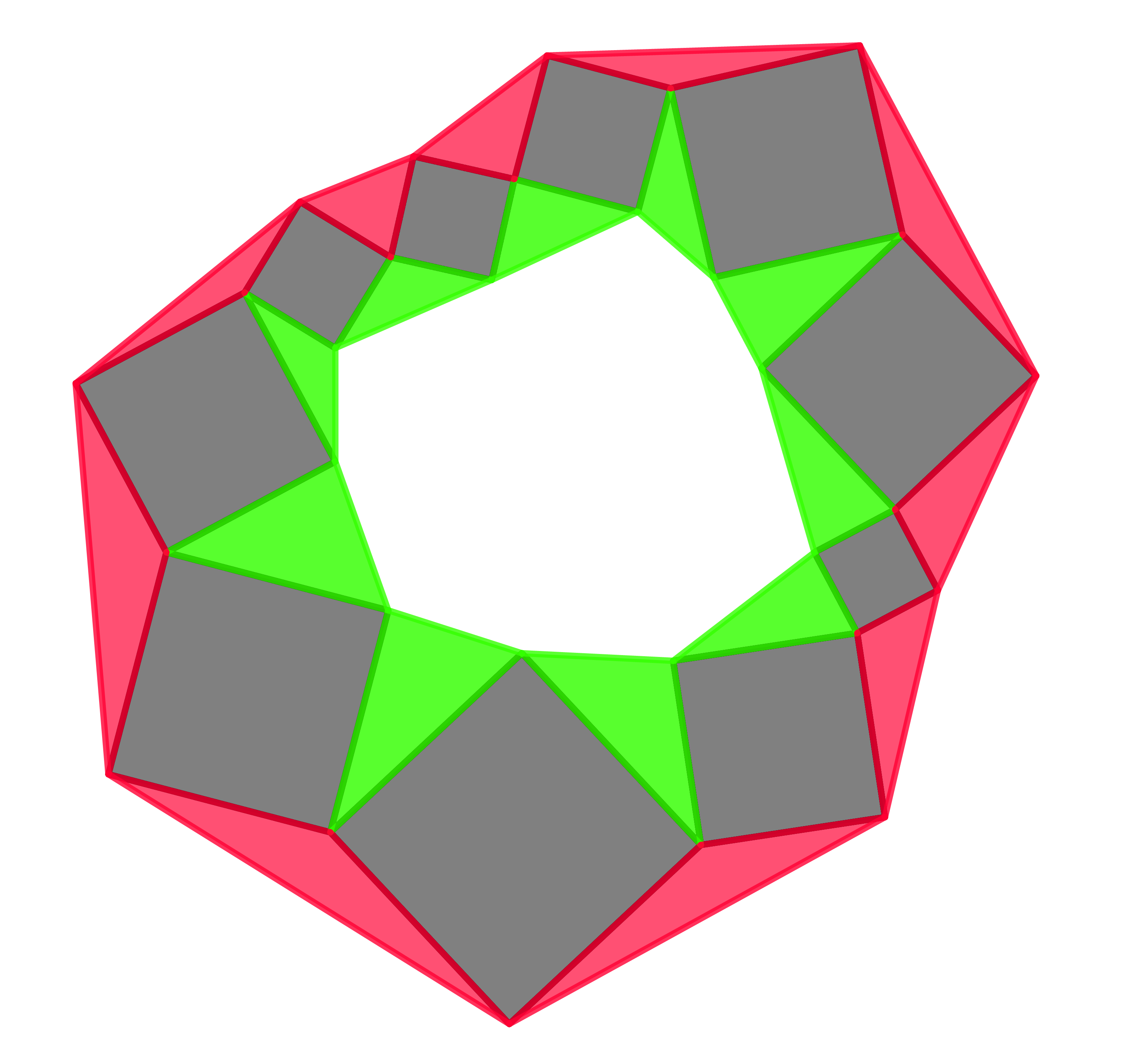
A series of squares are connected by touching vertices. Some triangles were drawn outside and inside of the chain. Show that the total green area is the same as the total red area.
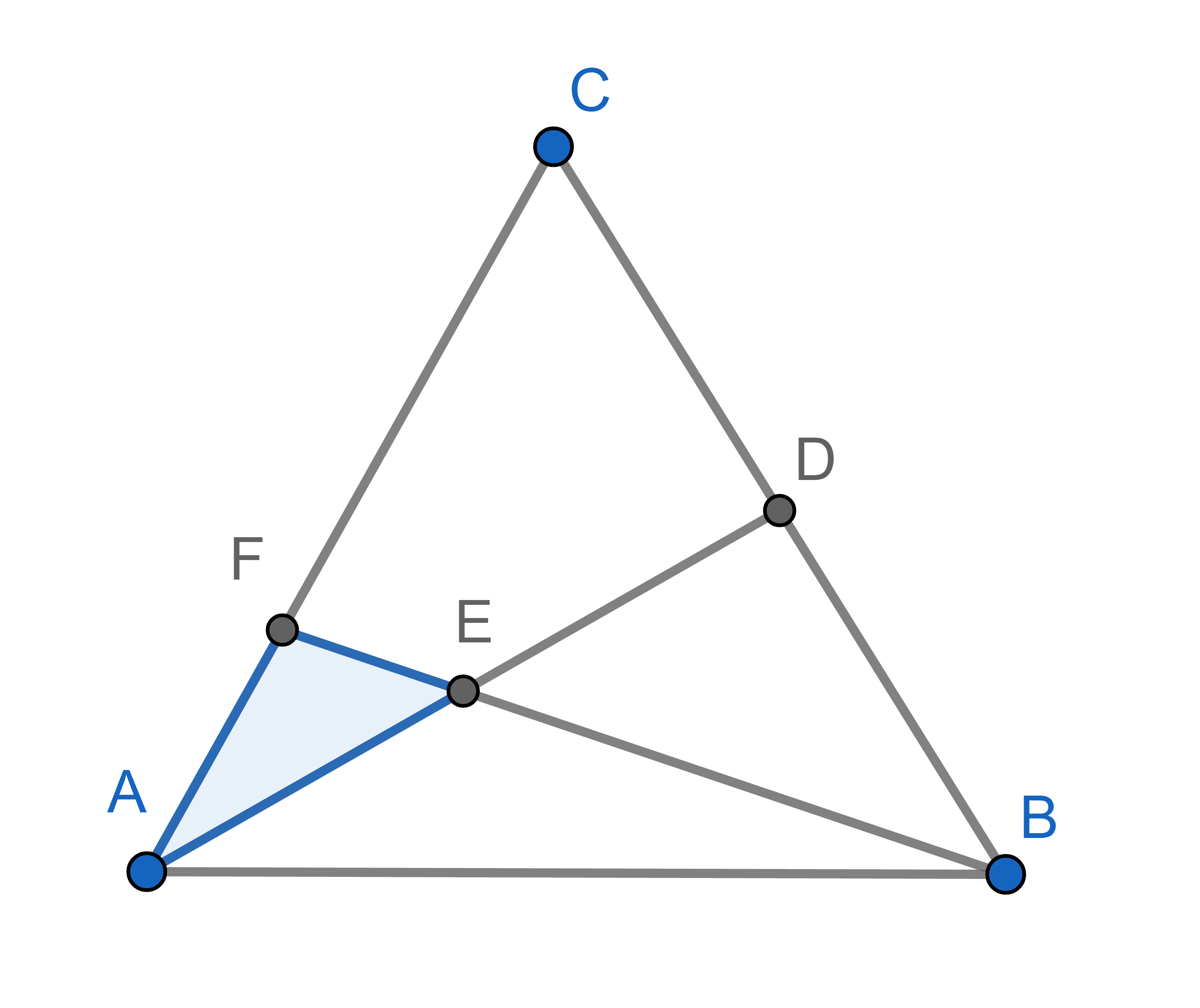
In a triangle \(\triangle ABC\), \(D\) is the midpoint of \(BC\), and \(E\) is the midpoint of \(AD\). \(F\) is the intersection of the side \(AC\) with \(BE\). What is the area of the triangle \(\triangle AEF\) as a proportion of the area of the triangle \(\triangle ABC\)?
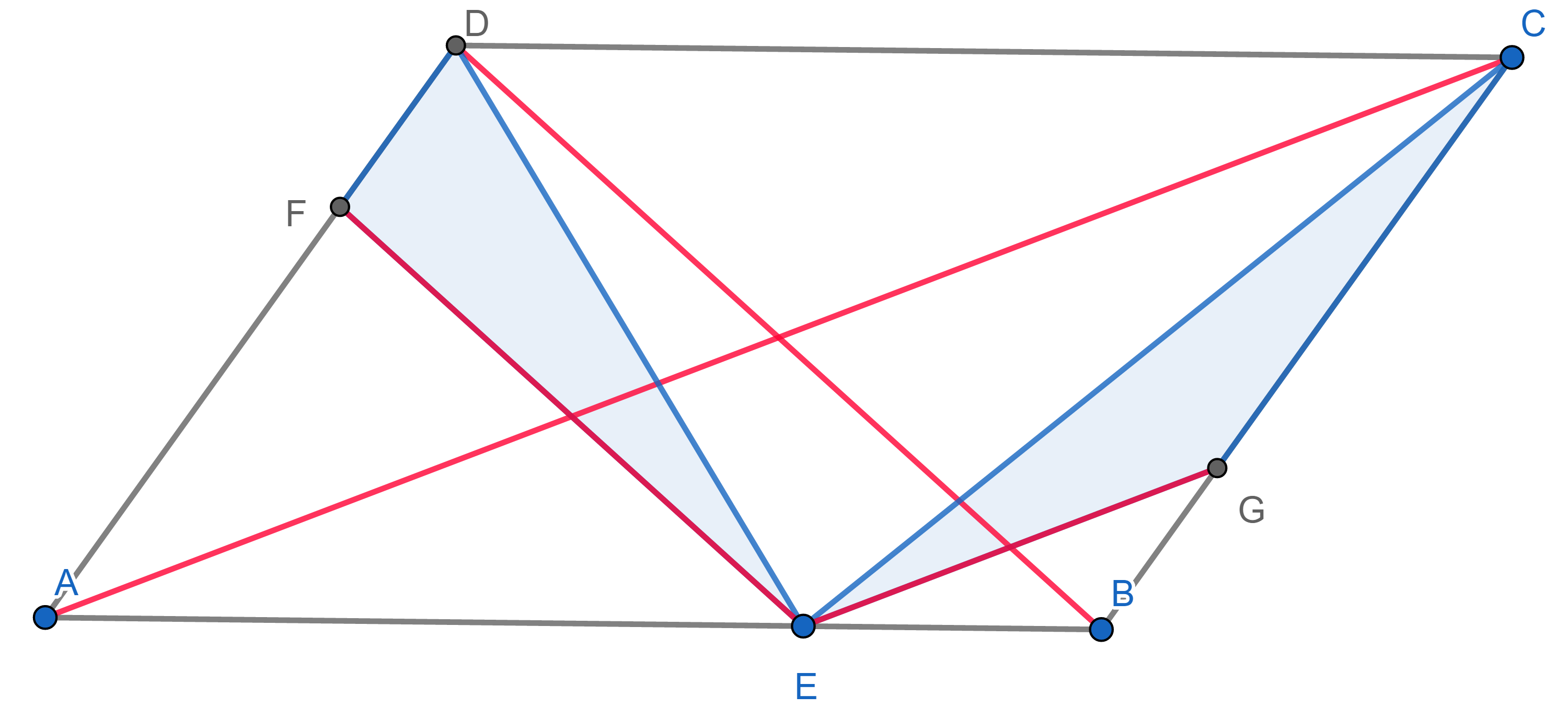
Let \(ABCD\) be a parallelogram. The segment \(EF\) is parallel to the diagonal \(BD\), and the segment \(EG\) is parallel to the diagonal \(AC\). Show that the areas of the triangles \(\triangle EFD\) and \(\triangle EGC\) are equal.
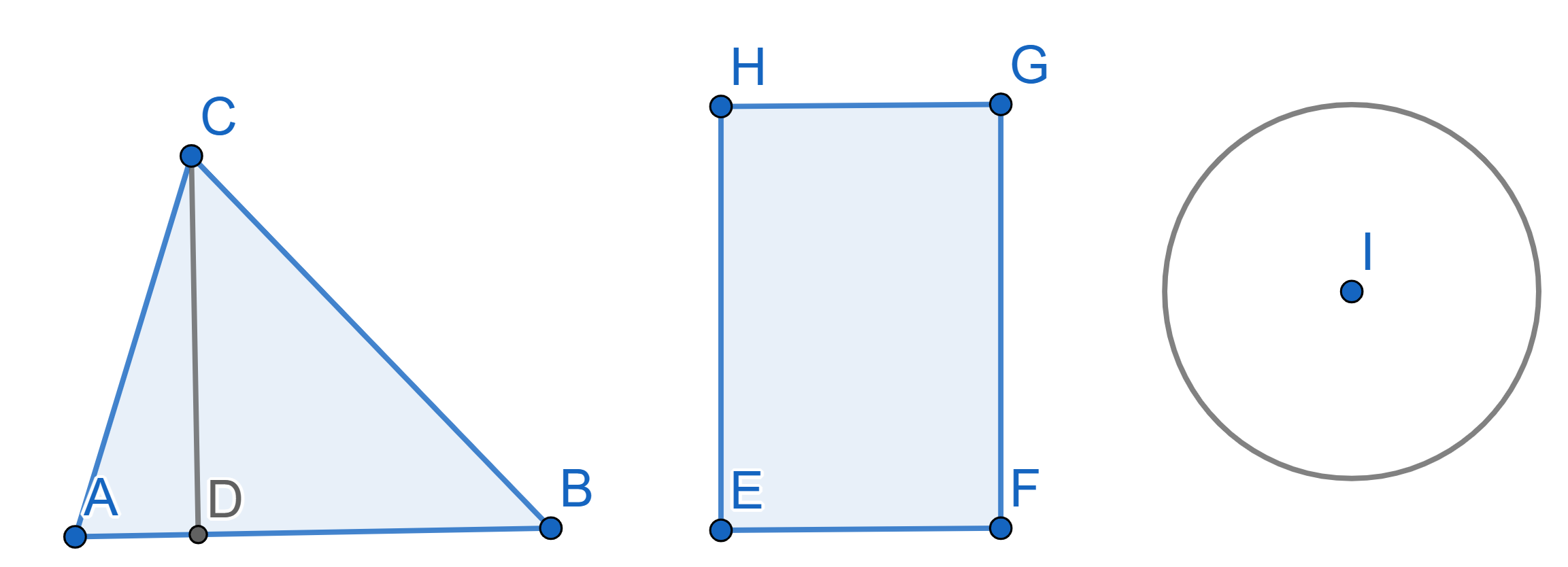
Today we will solve some problems about finding areas of geometric figures. All you need to know in order to solve every problem in this set is: to calculate the area of a triangle we multiply the length of a side by the length of a height to that side and divide by \(2\), namely:\(\frac12 AB \times CD\), as for rectangle we just multiply two adjacent sides (\(EF \times GF\)), and when we have a circle we calculate the area by \(\pi r^2\), where \(r\) is the radius of the circle.
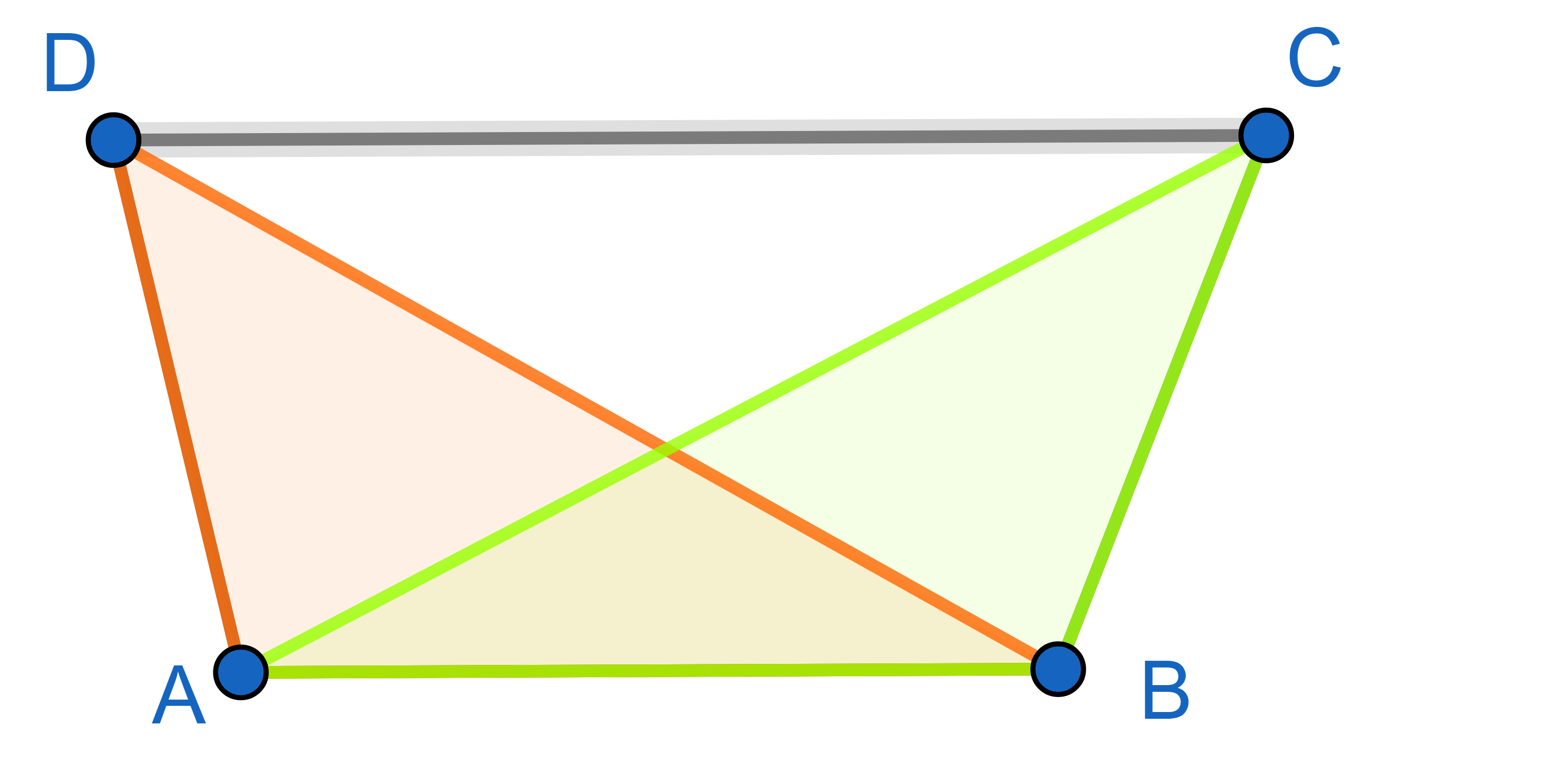
In a trapezium \(ABCD\), the side \(AB\) is parallel to the side \(CD\). Prove that the areas of triangles \(\triangle ABC\) and \(\triangle ABD\) are equal.
On the left there is a circle inscribed in a square with side \(1\). On the right there are \(16\) smaller, identical circles, which all together fit inside a square of side \(1\). Which area is greater, the yellow or the blue one?

