Problems
Katie and Charlotte had \(4\) sheets of paper. They cut some of the sheets into \(4\) pieces. They then cut some of the newly obtained papersheets also into \(4\) pieces. They did this several more times, cutting a piece of paper into \(4\). In the end they counted the number of sheets. Could this number be \(2024\)?
There is a scout group where some of the members know each other. Amongst any four members there is at least one of them who knows the other three. Prove that there is at least one member who knows the entirety of the scout group.
The distance between two villages equals \(999\) kilometres. When you go from one village to the other, every kilometre you see a sign on the road, saying \(0 \mid 999, \, 1\mid 998, \, 2\mid 997, ..., 999\mid 0\). The signs show the distances to the two villages. Find the number of signs that contain only two different digits. For example, the sign \(0\mid999\) contains only two digits, namely \(0\) and \(9\), whereas the sign \(1\mid998\) contains three digits, namely \(1\), \(8\) and \(9\).
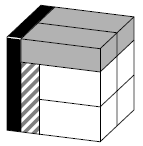
Michael made a cube with edge \(1\) out of eight bars as in the picture. All \(8\) bars have the same volume. The dimensions of the grey bars are the same as each other. Similarly, the dimensions of the white bars are the same as each other. Find the lengths of the edges of the white bars.
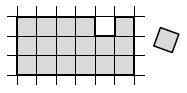
One cell was cut out of a \(3\times6\) rectangle, as seen in the diagram. How should you glue this cell in a different place to get a figure that can be cut into two identical ones? If needed, the resulting parts can be rotated and reflected.
In the sum below, different letters denote different digits and the same letters denote the same digit. \[P.Z + T.C + D.R + O.B + E.Y\] None of the five terms are integers, but the sum itself is an integer. Find the possible sums of the expression. For each possible answer, write one example with these five terms. Explain why other sums cannot be obtained.
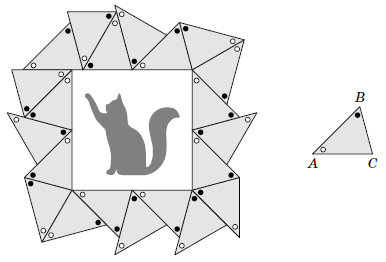
Peter went to the Museum of Modern Art and saw a square painting in a frame of an unusual shape. The frame consisted of \(21\) congruent triangles. Peter was interested in what the angles of these triangles were equal to. Help him find these angles.
Red, blue and green chameleons live on an island. One day \(35\) chameleons stood in a circle. A minute later, they all changed colour at the same time, each changing into the colour of one of their neighbours. A minute later, everyone again changed their colours at the same time into the colour of one of their neighbours. Is it ever possible that each chameleon was each of the colours red, blue and green at some point? For example, it’s allowed for a chameleon to start off blue, turn green after one minute, then turn red after the second minute. It’s not allowed for a chameleon to start off blue, turn green after one minute, but then turn back to blue after the second minute.
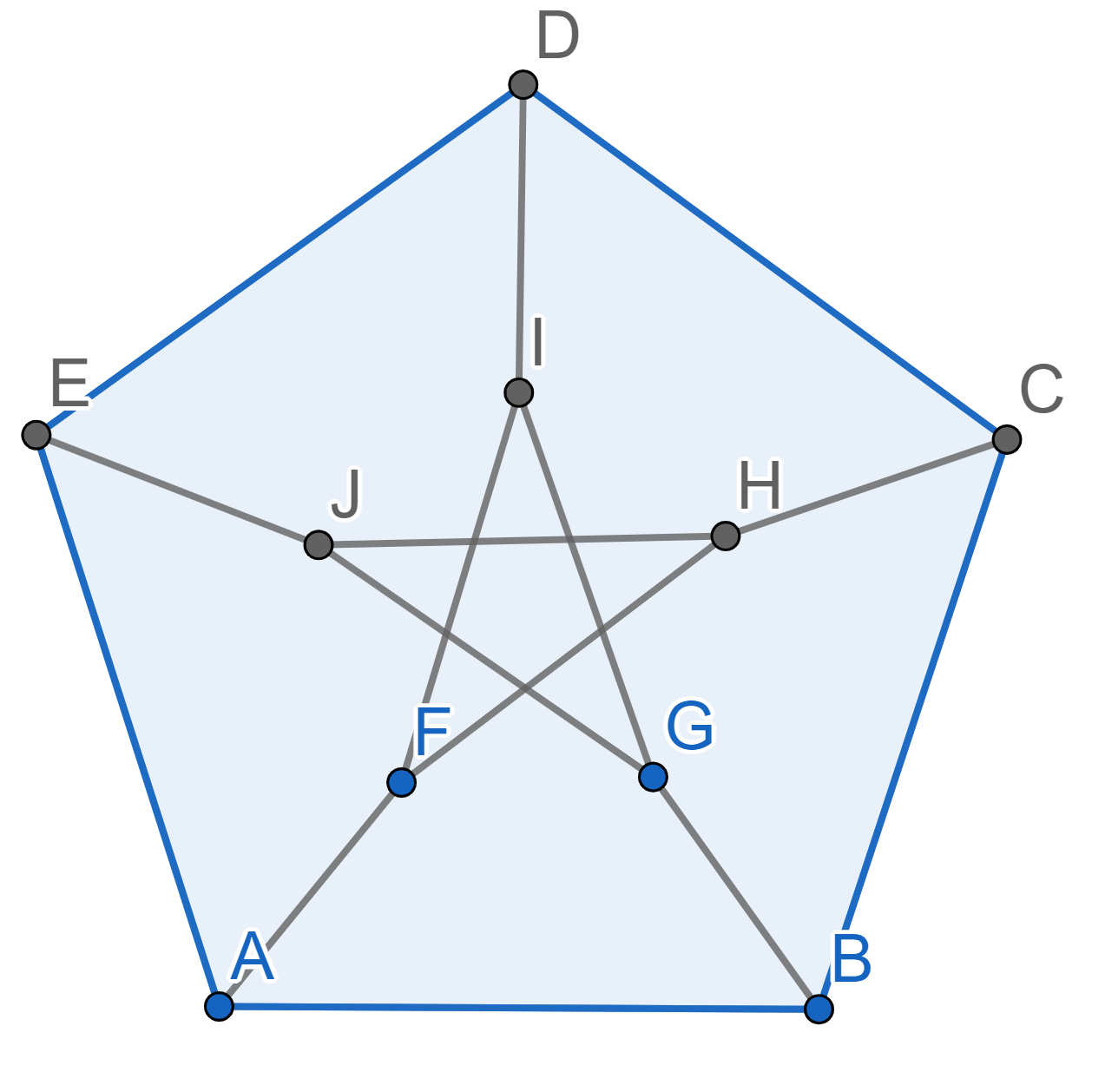
We want to color each of the 15 segments in the picture below using three colors. We need to color them so that if two segments share a point, then they are not the same color. For example, you cannot have both \(AB\) and \(BC\) be blue since they share the end \(B\). Is such a painting possible?
In an \(n\times n\) table, two opposite corner squares are black and the rest are white. We wish to turn the whole \(n\times n\) table black in two stages. In the first stage, we paint black some of the squares that are white at the moment. In the second stage, we can perform the following two operations as much as we like. The row operation is to swap the colours of all the squares in a particular row. The column operation is to swap the colours of all the squares in a particular column. What is the fewest number of white squares that we can paint in the first stage?
An example of the row operation: let W stand for white and B stand for black and suppose that \(n=5\). Also suppose that a particular row has the colours WWBWB. Then performing the row operation would change this row to BBWBW.