Problems
Imagine the Earth is a perfectly round solid ball. Let us drill from the North Pole, London and Beijing simultaneously and meet at the centre of Earth. A ball with three openings is formed. The surface of this ball is shown on the left of the picture below. Describe how to stretch this surface so that it looks like the surface of a donut with two holes as shown on the right.
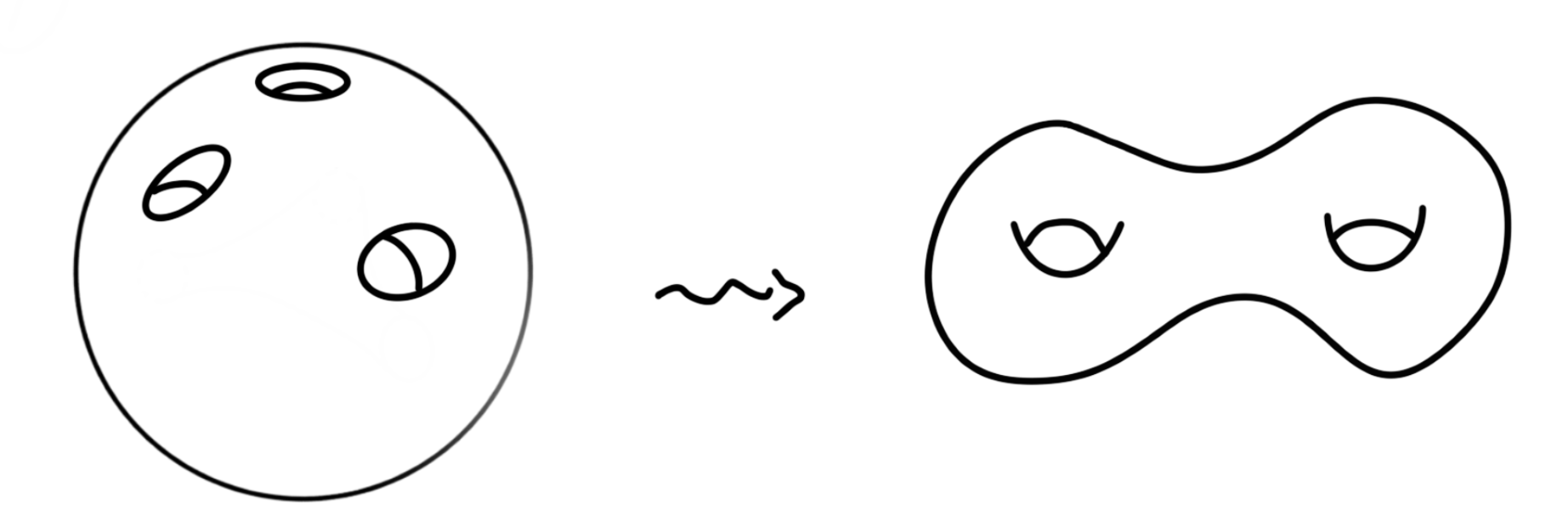
The unknot is the simplest knot, formed by taking a piece of straight string and gluing its two ends together. In reality, there is no knot! Now, which of the following two knots is the unknot?
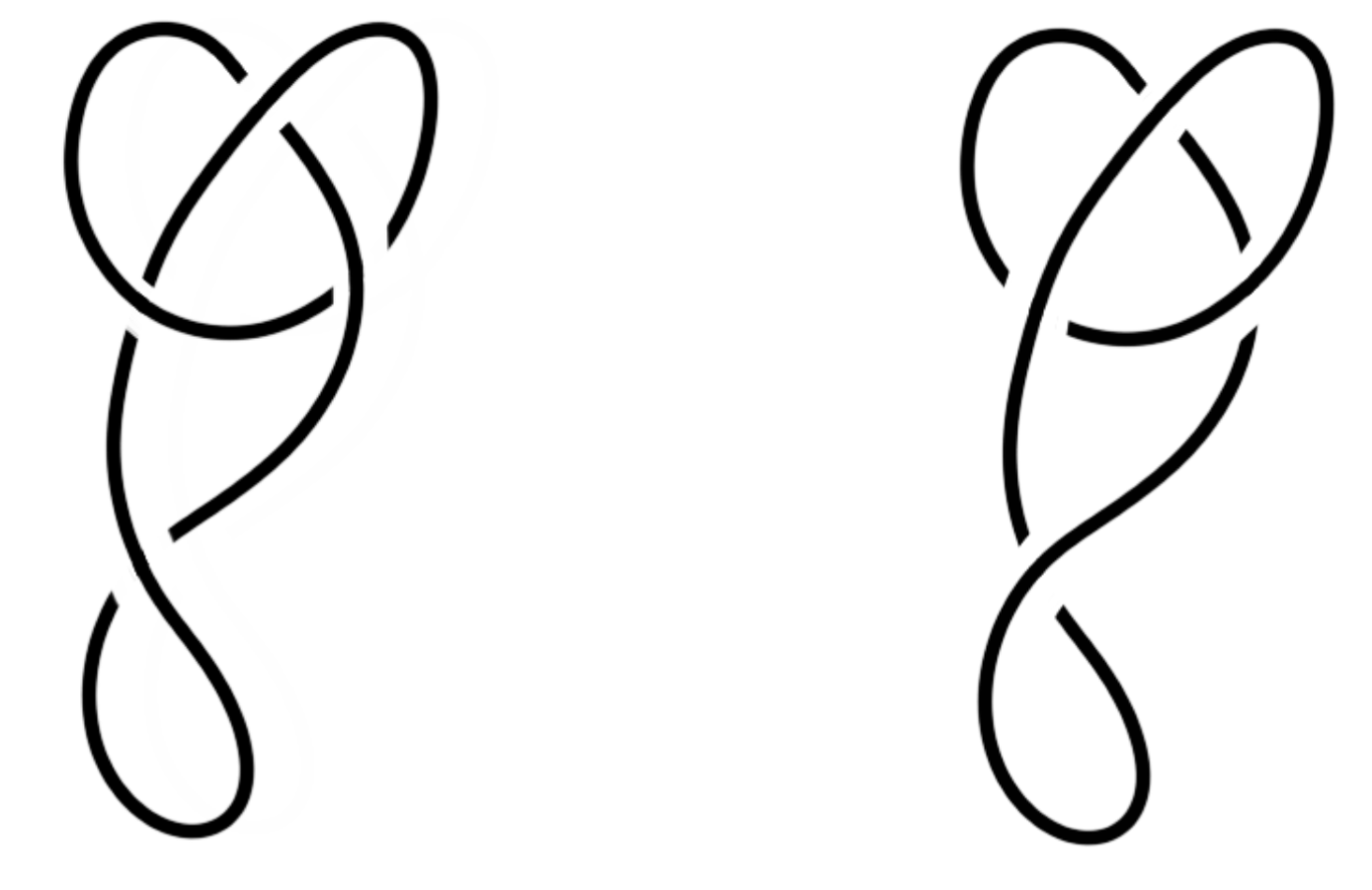
Show that a knot that can be drawn with only one crossing must be the unknot.
How do you go from the left figure to the right one without cutting, tearing or passing the strings through each other? The blue object consist of two circles glued together at a point.
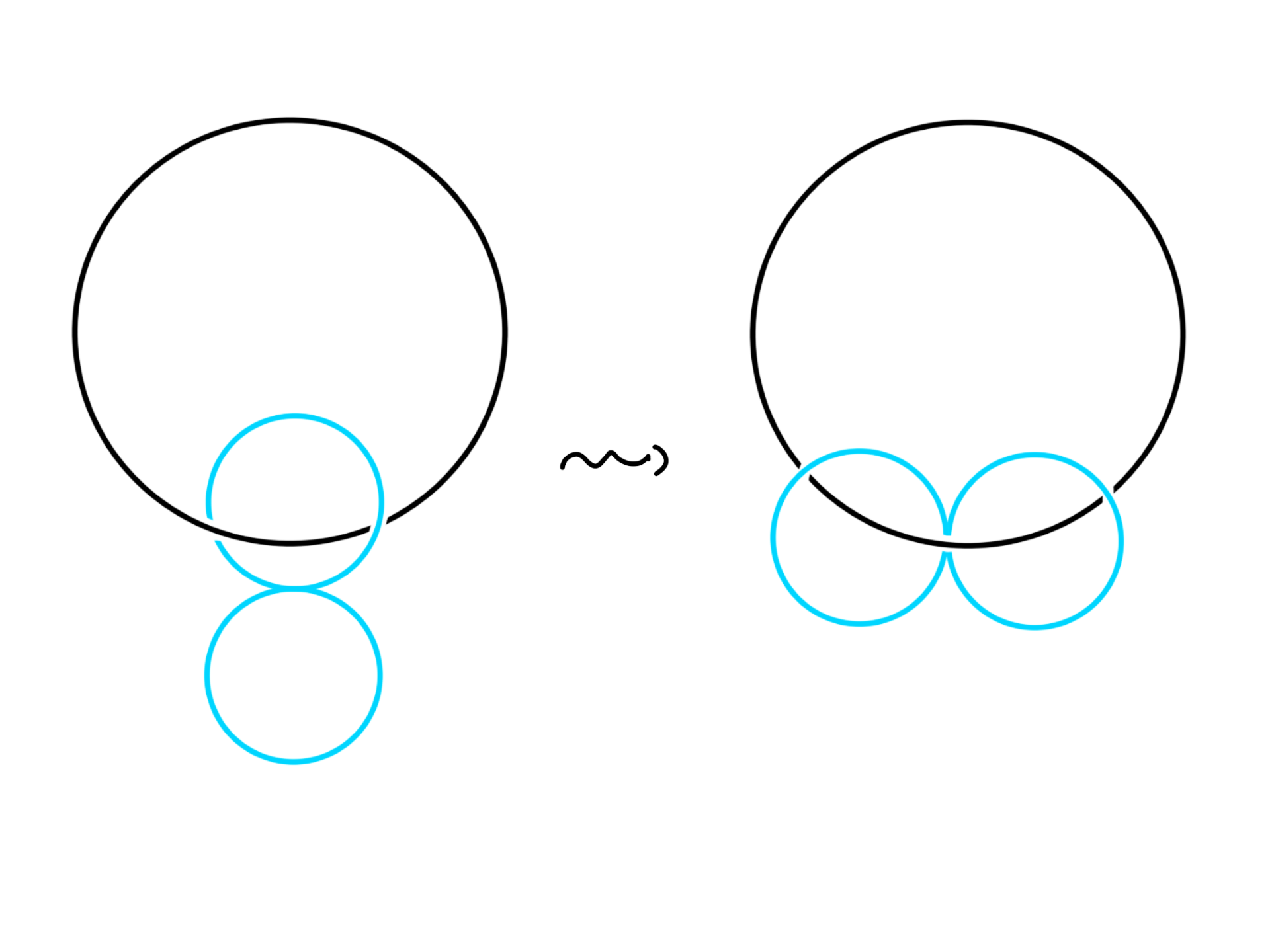
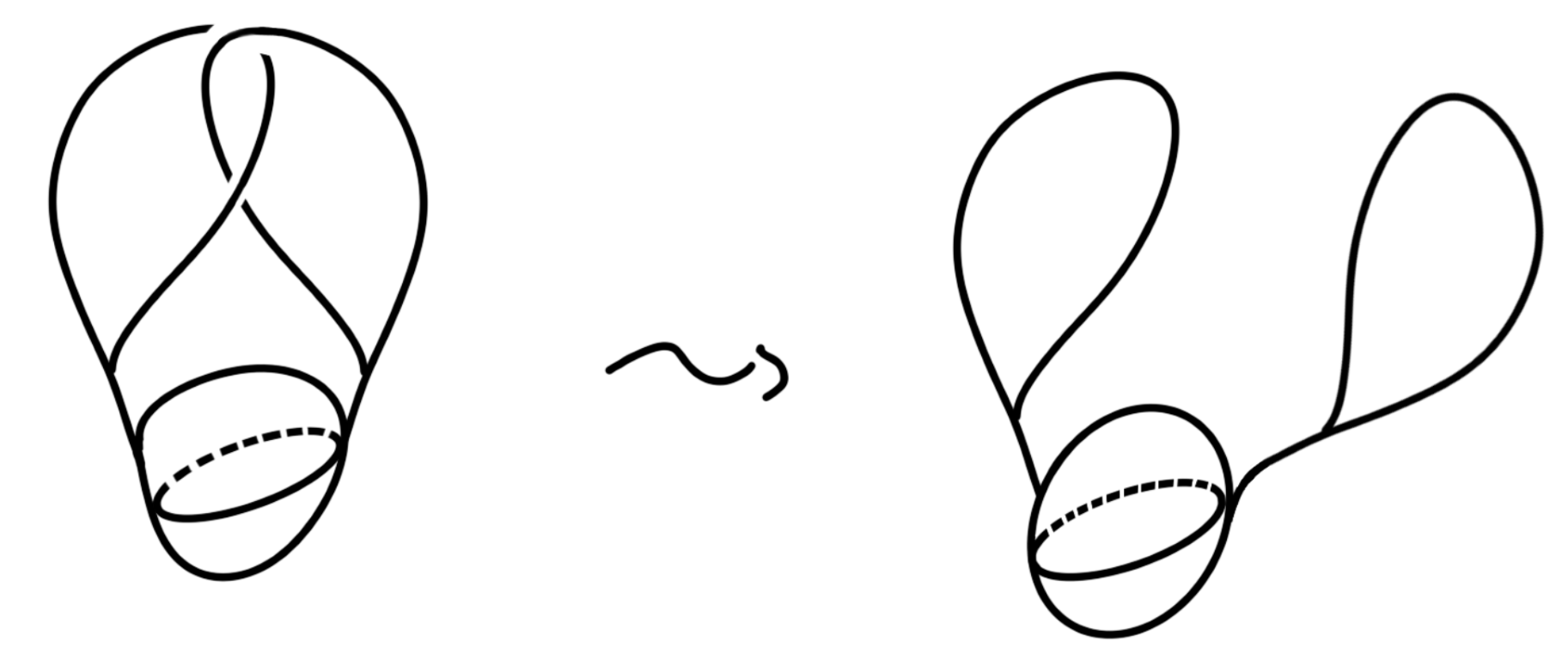
The left figure is formed by two interlocking loops joined to a solid ball. The right figure is formed by two unlinked loops joined to a solid ball. Describe how to transform the left into the right without cutting, tearing or passing the loops through each other.
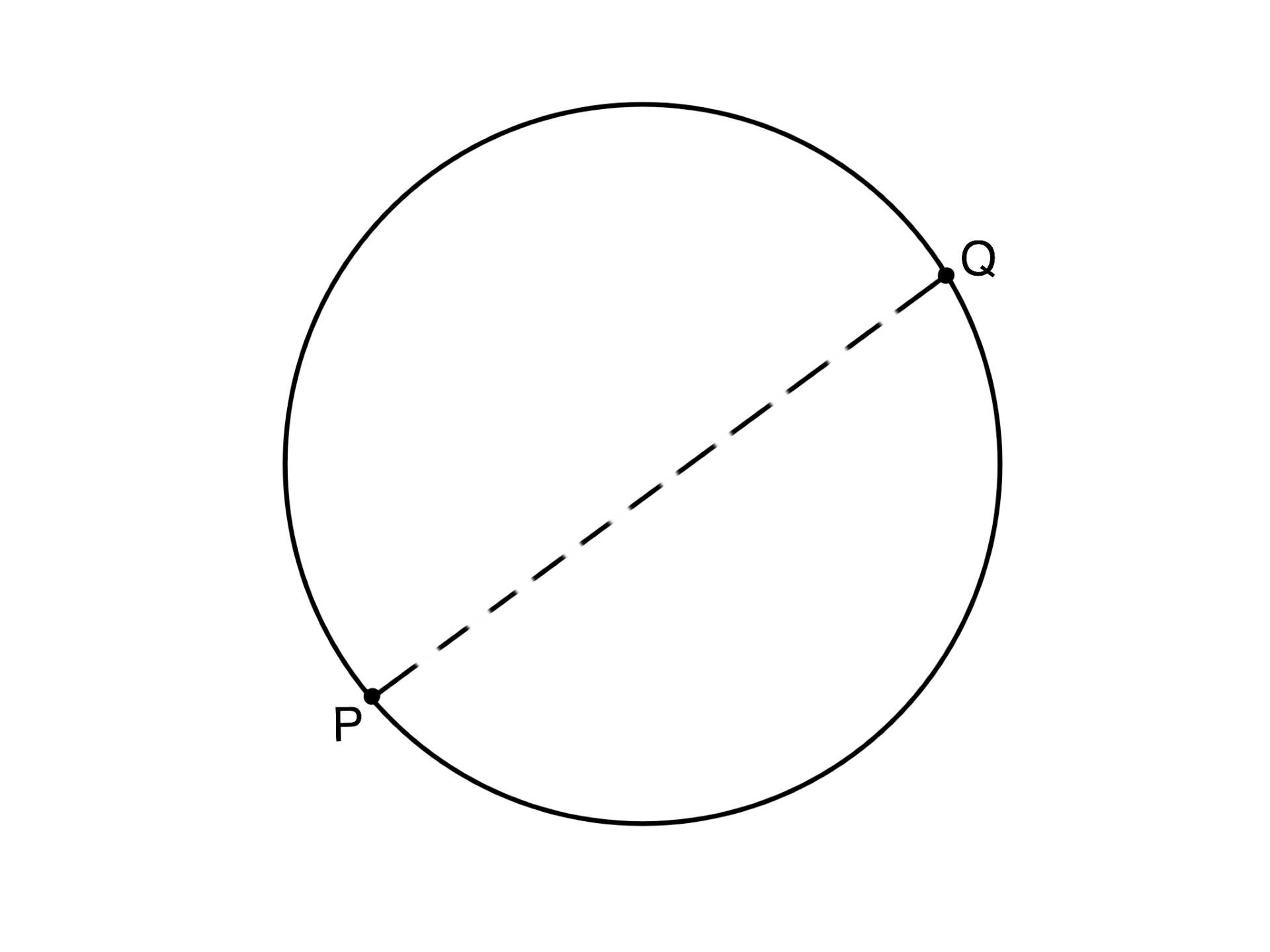
A pair of points on a circle are said to be antipodal if they are on two opposite ends of a common diameter. P and Q in the picture are antipodal points. If we glue every pair of antipodal points on a circle, then what is the resulting shape?
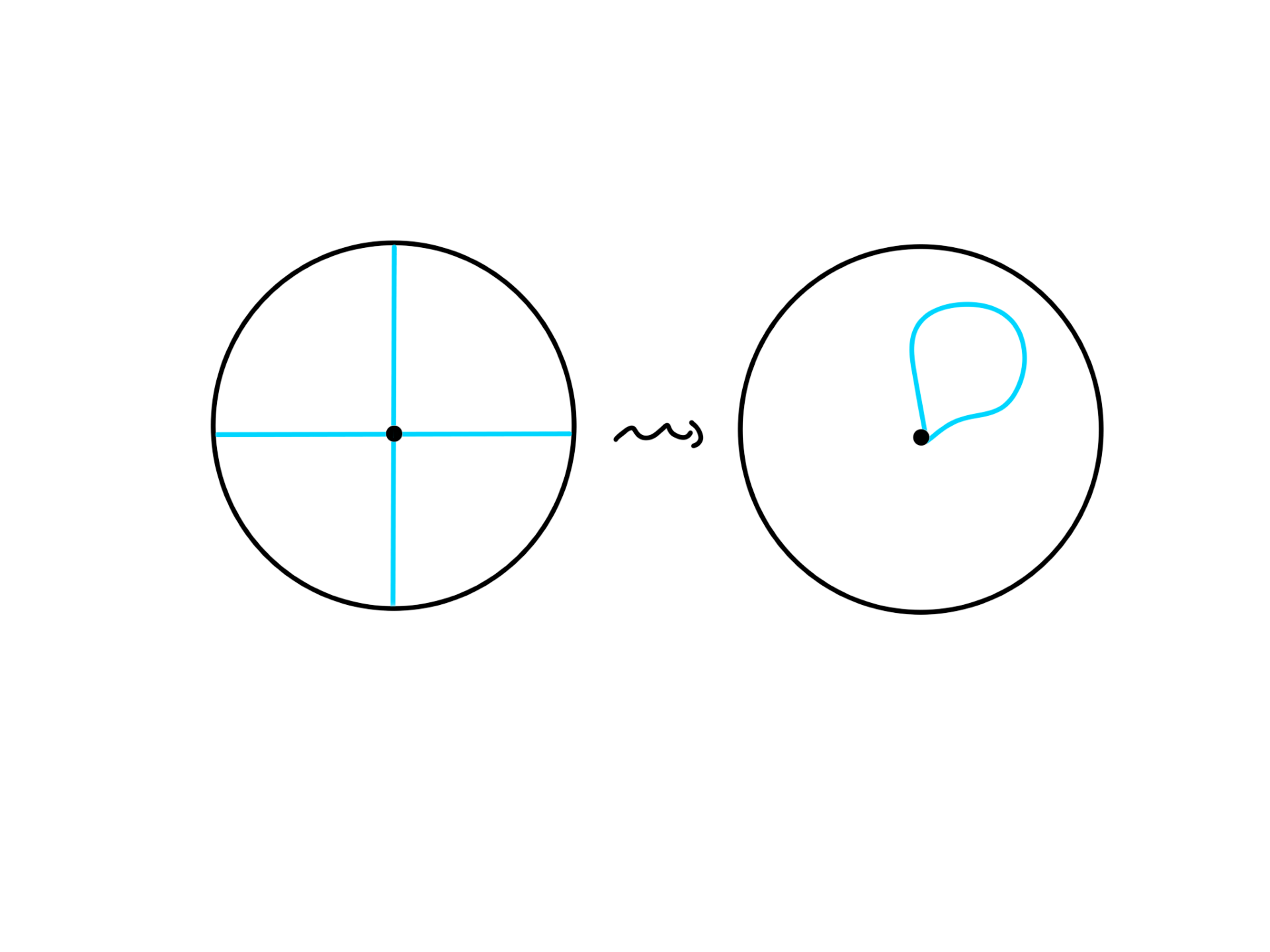
A surface P is created by gluing every pair of antipodal points of a disc (a circle with inside filled in). We represent P on the plane by a disc in the following picture and bear in mind that the antipodal points are glued.
Explain why the two diameters in the pictures are in fact two circles on P and how to stretch it so that it becomes a single loop not touching any of the glued points.
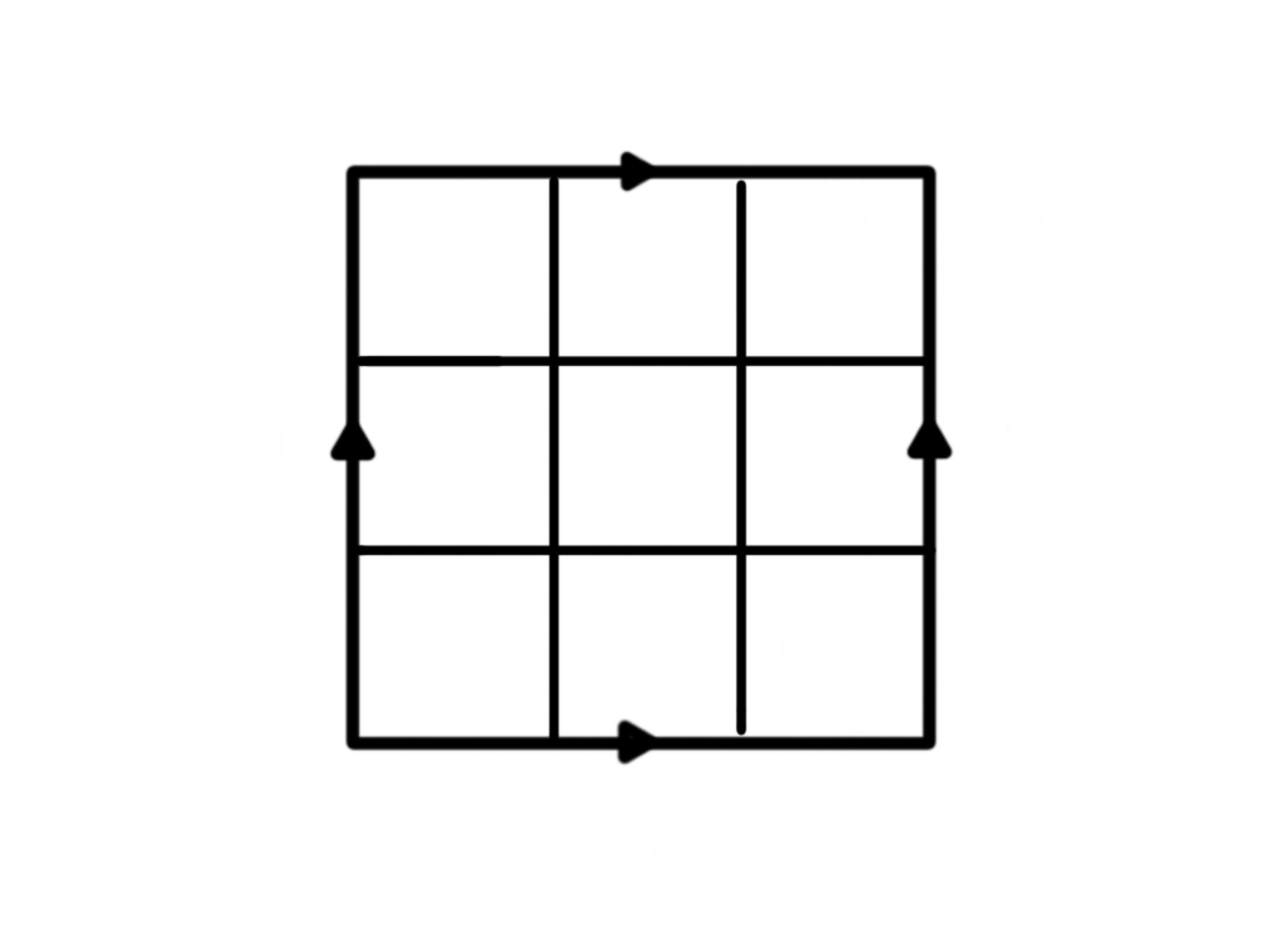
It is possible to play tic-tac-toe on a torus: gluing the sides means that the bottom row is above the top row and the right most column is also to the left of the left most column. Is one of the players guaranteed to win if they play all the right moves?
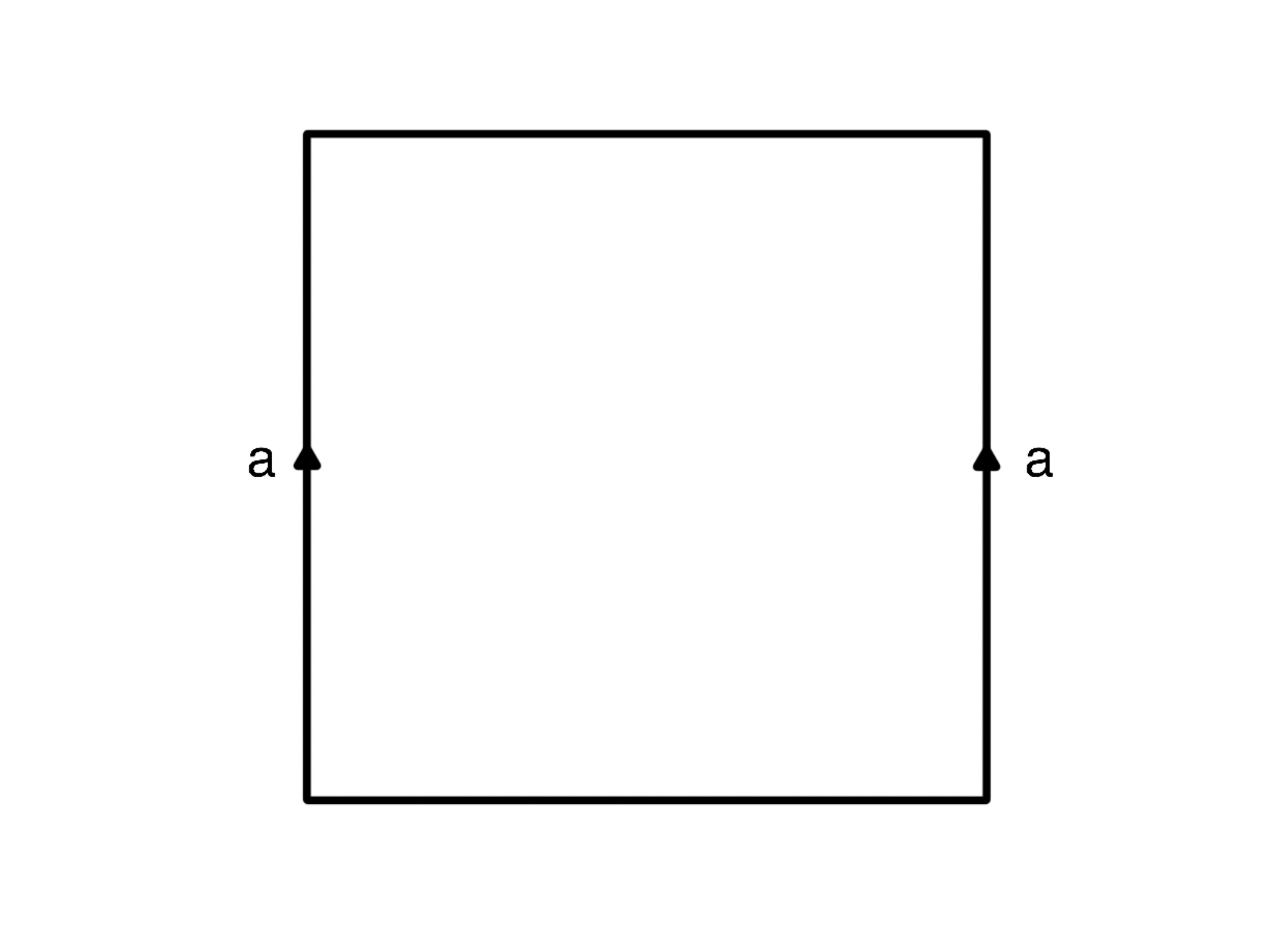
Describe the surface we get if we start with a rectangular sheet of paper and then glue the opposite sides of the paper band in the same direction as in the picture.
Show that there are no rational numbers \(a,b\) such that \(a^2 + b^2 = 3\).