Problems

An animal with \(n\) cells is a connected figure consisting of \(n\) equal-sized adjacent square cells. A dinosaur is an animal with at least 2007 cells. It is said to be primitive if its cells cannot be partitioned into two or more dinosaurs. Find with proof the maximum number of cells in a primitive dinosaur.

Remainder is the number that is “left over" from division. Even if a number is not divisible by another number fully, we can still divide, but leaving a remainder. The remainder is less than the number we’re dividing by. For example, a remainder of \(44\) in division by \(7\) is \(2\), because \(44 = 6 \times 7 + 2\). More generally, we can write \(n=qk+r\), where \(0\leq r<k\). We say that \(k\) goes into \(n\) \(q\) times, and a little bit (\(r\)) is left. If that little bit was larger than \(k\), it could “go into" \(n\) once more.

The general rule is that a remainder of a sum, difference or a product of two remainders is equal to the remainder of a sum, difference or a product of the original numbers. What that means is if we want to find a remainder of a product of two numbers, we need to look at the individual remainders, multiply them, and then take a remainder.

For example, \(10\) has remainder \(3\) when dividing by \(7\) and \(11\) has remainder \(4\) when dividing by \(7\). The product \(10\times11=110\) will have the same remainder as the product of the individual remainders. We first multiply \(3\times4=12\) and then take a remainder upon division by \(7\), which is \(5\) because \(12=7+5\). That means that \(110\) gives a remainder \(5\) in division by \(7\) - and it does, because \(110=15\times7+5\). If a number is divisible by a number we are dividing it, nothing remains and we say the remainder is \(0\).

Let’s have a look on some examples:

What time is it going to be in \(2025\) hours from now?

Prove that the product of five consecutive integers is divisible by \(30\).

Prove that if \(n\) is a composite number, then \(n\) is divisible by some natural number \(x\) such that \(1 < x\leq \sqrt{n}\).

The natural numbers \(a,b,c,d\) are such that \(ab=cd\). Prove that the number \(a^{2025} + b^{2025} + c^{2025} + d^{2025}\) is composite.

Prove that for an arbitrary odd \(n = 2m - 1\) the sum \(S = 1^n + 2^n + ... + n^n\) is divisible by \(1 + 2 + ... + n = nm\).

Certain geometric objects nicely blend when they happen to be together in a problem. One possible example of such a pair of objects is a circle and an inscribed angle.
We will be using the following statements in the examples and problems:
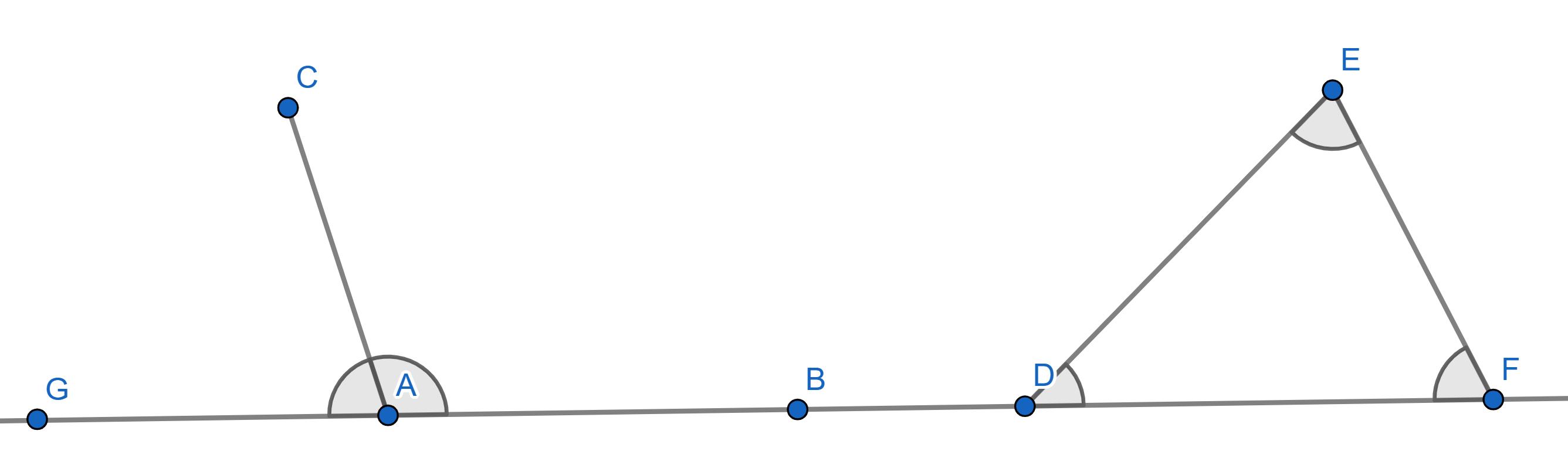
1. The supplementary angles (angles “hugging" a straight line) add up to \(180^{\circ}\).
2. The sum of all internal angles of a triangle is also \(180^{\circ}\).

3. Two triangles are said to be “congruent" if ALL their corresponding sides and angles are equal.
We recommend solving the problems in this sheet in the order of appearance, as some problems use statements from previous problems as a step in the solution. Specifically, the inscribed angle theorem (problem 2) is required to solve every other problem that comes after it.

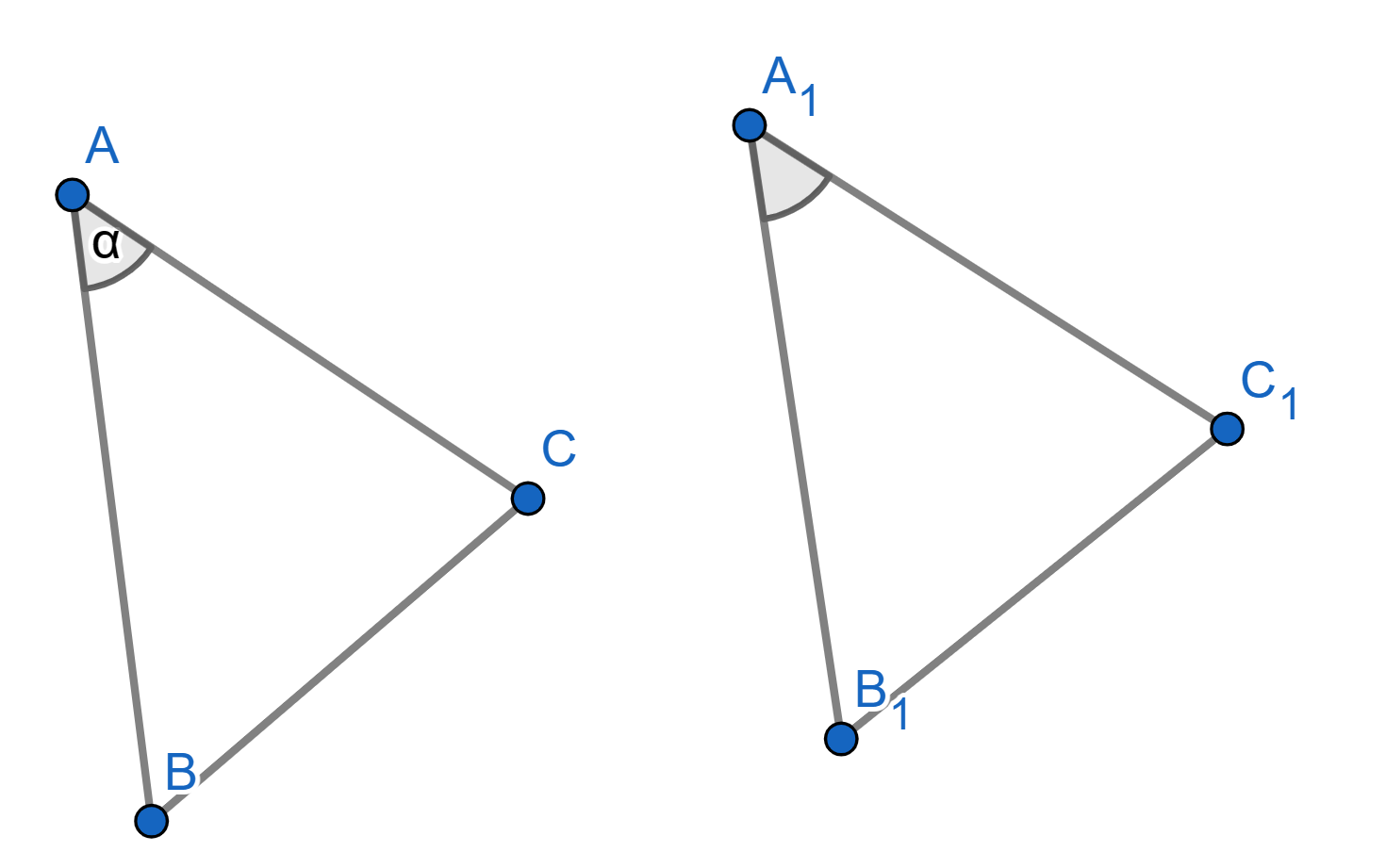
Let \(ABC\) and \(A_1B_1C_1\) be two triangles with the following properties: \(AB = A_1B_1\), \(AC = A_1C_1\), and angles \(\angle BAC = \angle B_1A_1C_1\). Then the triangles \(ABC\) and \(A_1B_1C_1\) are congruent. This is usually known as the “side-angle-side" criterion for congruence.

In the triangle \(\triangle ABC\) the sides \(AC\) and \(BC\) are equal. Prove that the angles \(\angle CAB\) and \(\angle CBA\) are equal.