Problems

A real number \(y\) is such that \(y+\frac1{y}\) happens to be an integer number. Show that for any natural \(n\), it is also true that \(y^n + \frac1{y^n}\) is an integer number.

DRAFT
We need to ensure that there isn’t overlap with the first areas problem sheet.
We can introduce the areas of a new shape, e.g. a trapezium more formally. Maybe an ellipse?

Previously, we have explored how to tile the plane using rectangles, but a much more fascinating topic is plane tilings with more intricate shapes such as quadrilaterals, pentagons, and even more unconventional shapes like chickens.
In this exercise sheet, we define a plane tiling as a covering of the entire plane, without any gaps or overlaps, using identical geometric shapes that can be rotated and symmetrical to each other. Usually, it is sufficient to cover a small portion of the plane with a particular pattern that can be extended to cover the entire plane.

Let’s start with covering the plane with triangles of the following shape.

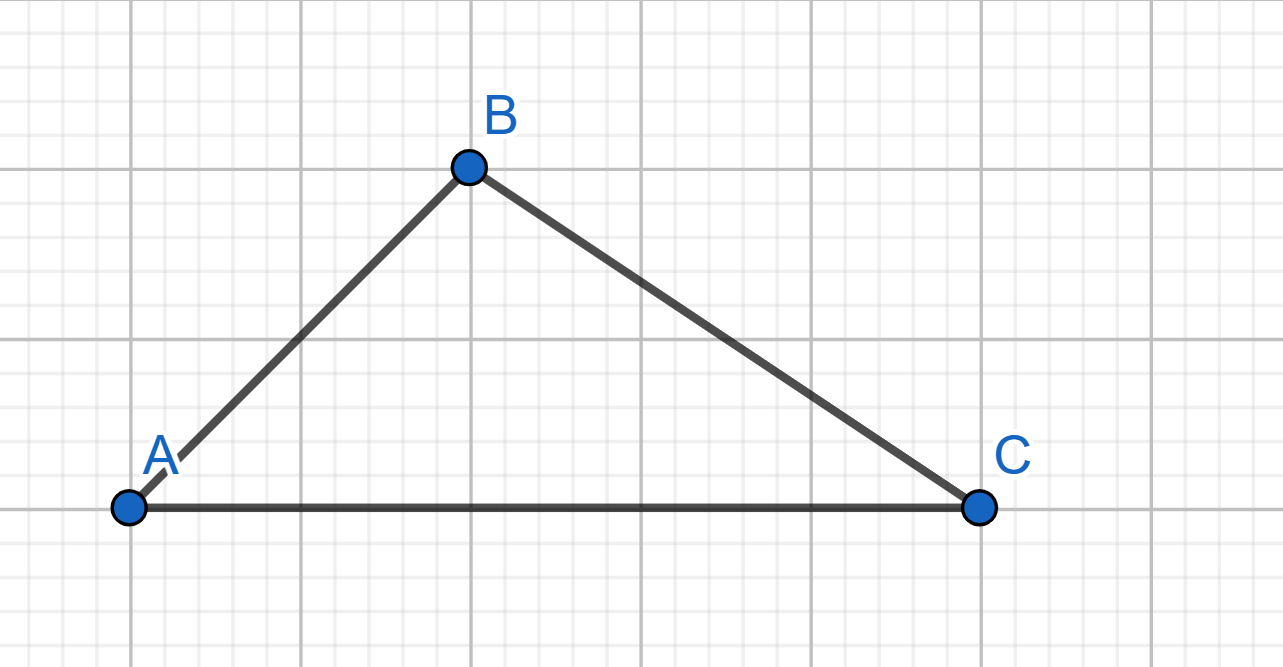
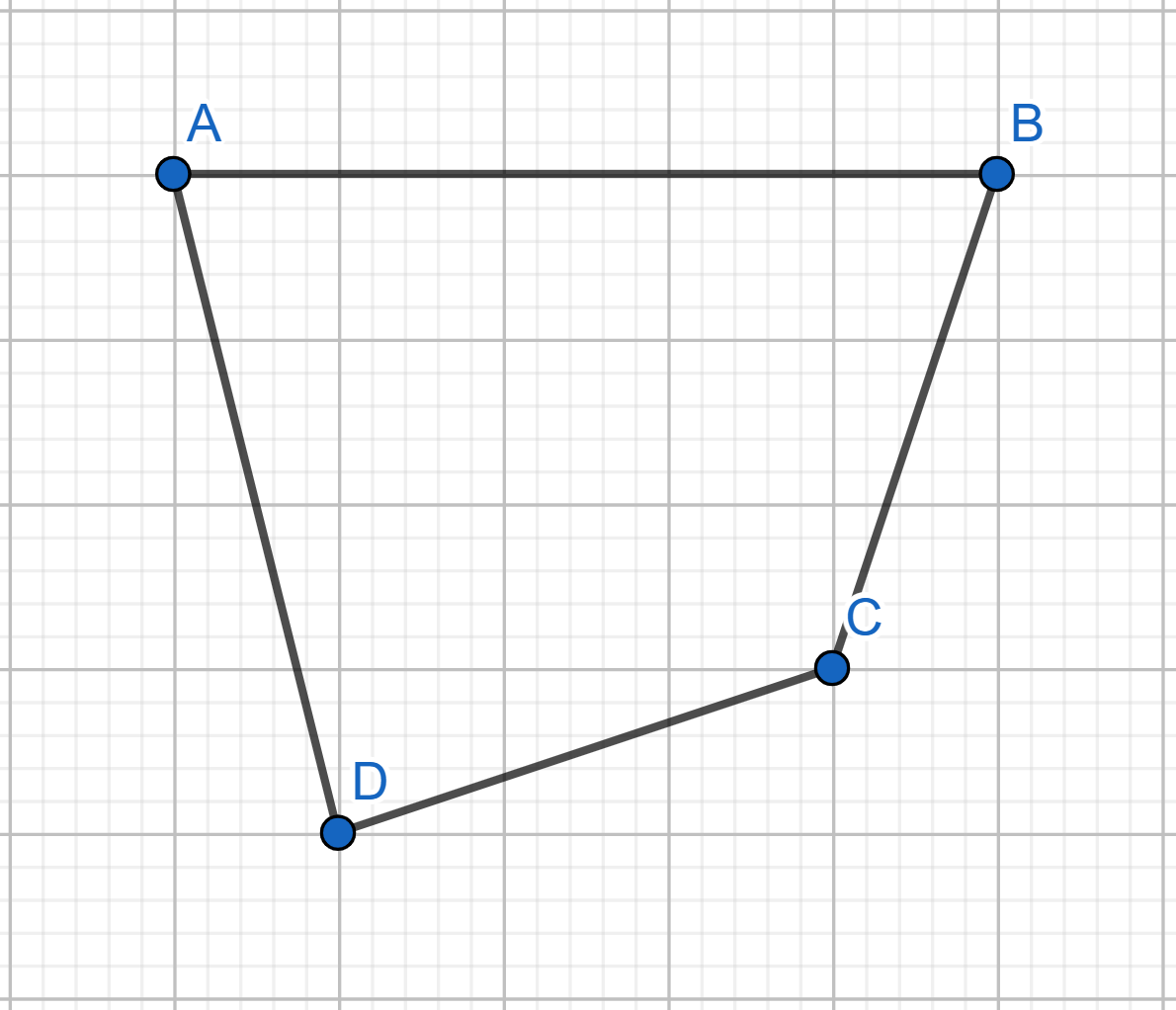
Now let’s try to cover the plane with convex quadrilaterals.

Draw how to tile the whole plane with figures, made from squares \(1\times 1\), \(2\times 2\), \(3\times 3\), and \(4\times 4\), where squares are used the same amount of times in the design of the figure.

Draw the plane tiling with:

• squares;

• rectangles \(1\times 3\);

• regular triangles;

• regular hexagons.

Draw the plane tiling using trapeziums of the following shape:

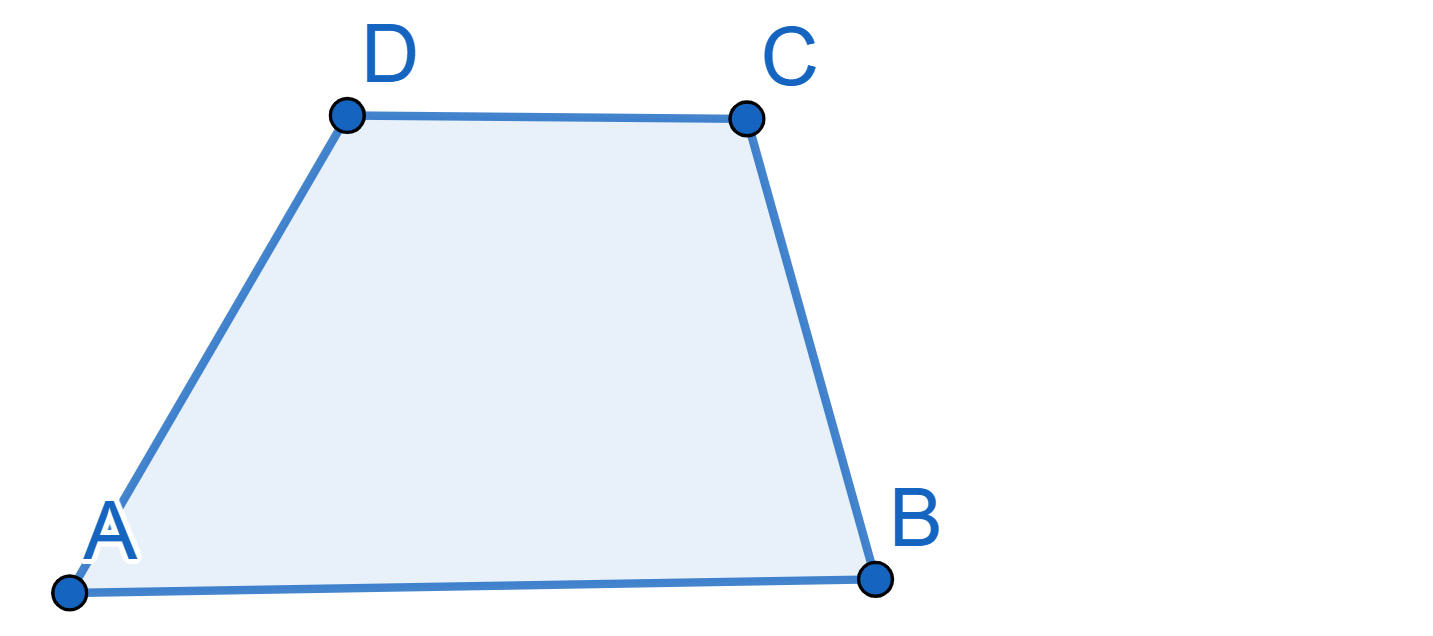
Here the sides \(AB\) and \(CD\) are parallel.

For any triangle, prove you can tile the plane with that triangle.

Prove that one can not tile the whole plane with regular pentagons.