Problems
Some Star Trek fans and some Doctor Who fans met at a science fiction convention. It turned out that everyone knew exactly three people at the convention. However, none of the Star Trek fans knew each other and none of the Doctor Who fans knew each other. Show that there are the same number of Star Trek fans as the number of Doctor Who fans at the convention.
Sometimes it is hard to rigorously formulate an intuitively correct reasoning. We might not know the proper words, the proper language, we might not have the right tools. Maths problems are not an exception. When we start learning to solve them, we know nothing about possible mathematical approaches and mathematical models. Today you will learn a very useful way to visualise information: you will learn how to represent information as a graph.
A graph is a finite set of points, some of which are connected with line segments. The points of a graph are called vertices. The line segments are called edges.
In a mathematical problem, one may use vertices of a graph to represent objects in the problem, i.e. people, cities, airports, etc, and edges of the graph represent relations between the objects such as mutual friendship, railways between cities, plane routes, etc. As you will see in the examples below, representing the initial problem as a graph can considerably simplify the solution.
Today we will solve some problems involving counting the same quantity twice (or more times) in different ways, which will let us learn about the components making it up.
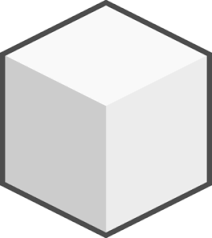
Starting at one of the vertices, an ant wishes to walk each of the \(12\) edges of a sugar cube exactly once. Prove that this is impossible.
Noah has \(10\) dogs, who he wishes
to group into \(5\) pairs for \(5\) families, each of whom want two dogs.
However, the dogs are quite picky, and can’t be paired with most of the
other dogs. None in the first group will go with each other: an
alsatian, a border collie, a chihuahua, a dachshund and an English
bulldog. None in the second group will go with each other: a foxhound, a
greyhound, a harrier, an Irish setter and a Jack Russell.
Furthermore,
The alsatian is the least picky and can be paired with any in the second
group.
The border collie won’t go with the foxhound, but will go with any other dog in the second group.
The chihuahua and the dachshund will only go with the Irish setter and the Jack Russell.
Additionally, none of the foxhound, greyhound and harrier will go
with the English bulldog.
Is it possible to pair up the \(10\)
dogs?
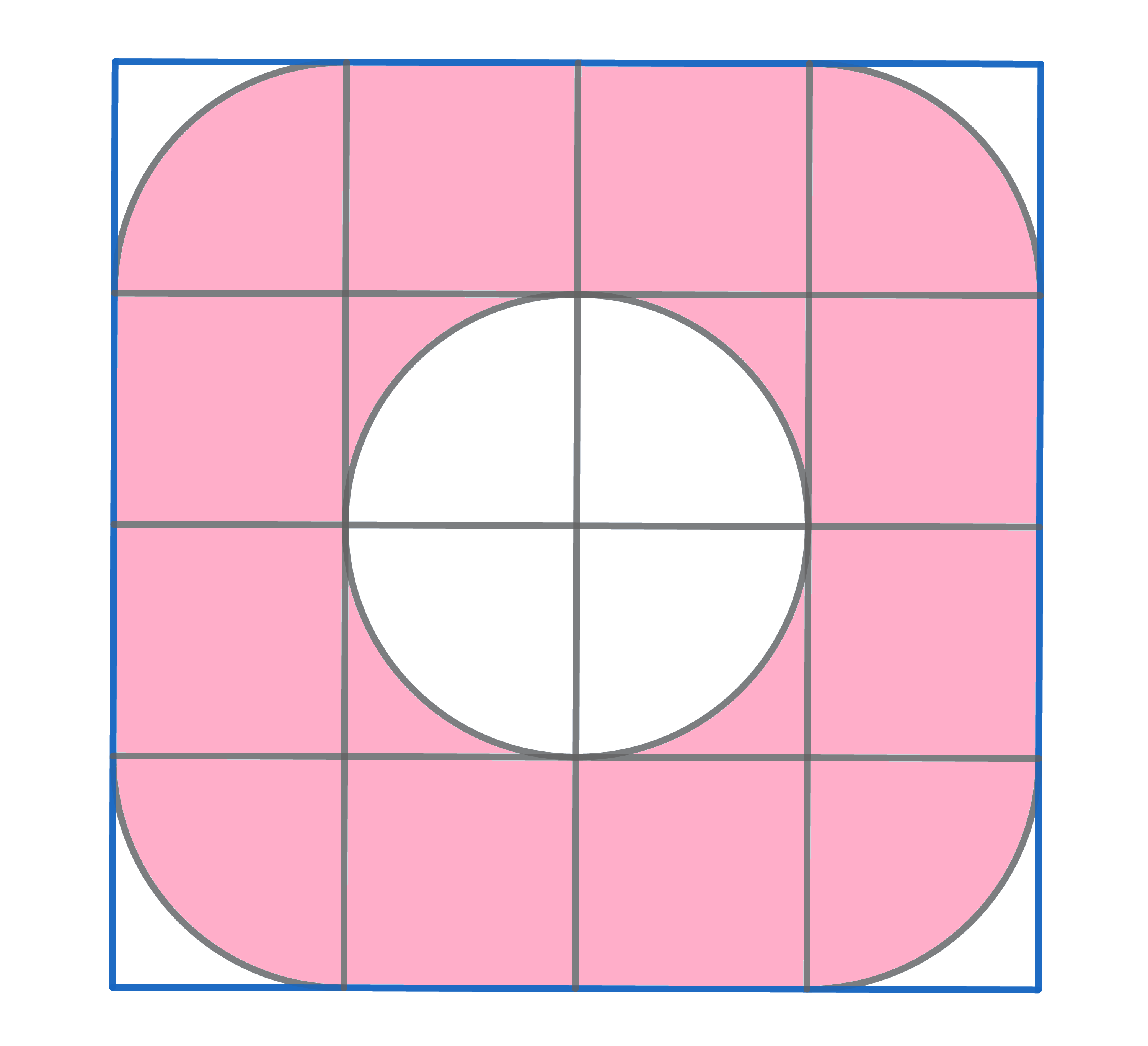
The area of the coloured figure equals \(48\)cm\(^2\). Find the length of the side of the smallest square.
The director of a bank has forgotten the combination to open the safe! He only remembers the first \(8\) out of \(10\) digits, and that the whole number was divisible by \(45\). Help him out and find all possible pairs of digits which could complete the combination. \[20242025**\]
There are two hourglasses, a small one and a large one. The sand in the small one takes \(7\) minutes to fall all the way through, and the sand in the large one takes \(11\) minutes. How can you measure \(15\) minutes using those?
Multiply an odd number by the two numbers either side of it. Prove that the final product is divisible by \(24\).
Mattia is thinking of a big positive integer. He tells you what this number to the power of \(4\) is. Unfortunately it’s so large that you tune out, and only hear that the final digit is \(4\). How do you know that he’s lying?