Problems
Let \(ABC\) be a triangle with midpoints \(D\) on the side \(BC\), \(E\) on the side \(AC\), and \(F\) on the side \(AB\). Let \(M\) be the point of intersection of all medians of the triangle \(ABC\), let \(H\) be the point of intersection of the heights \(AJ\), \(BI\) and \(CK\). Prove that the points \(D\), \(J\), \(I\), \(E\), \(F\) and \(K\) all lie on one circle.
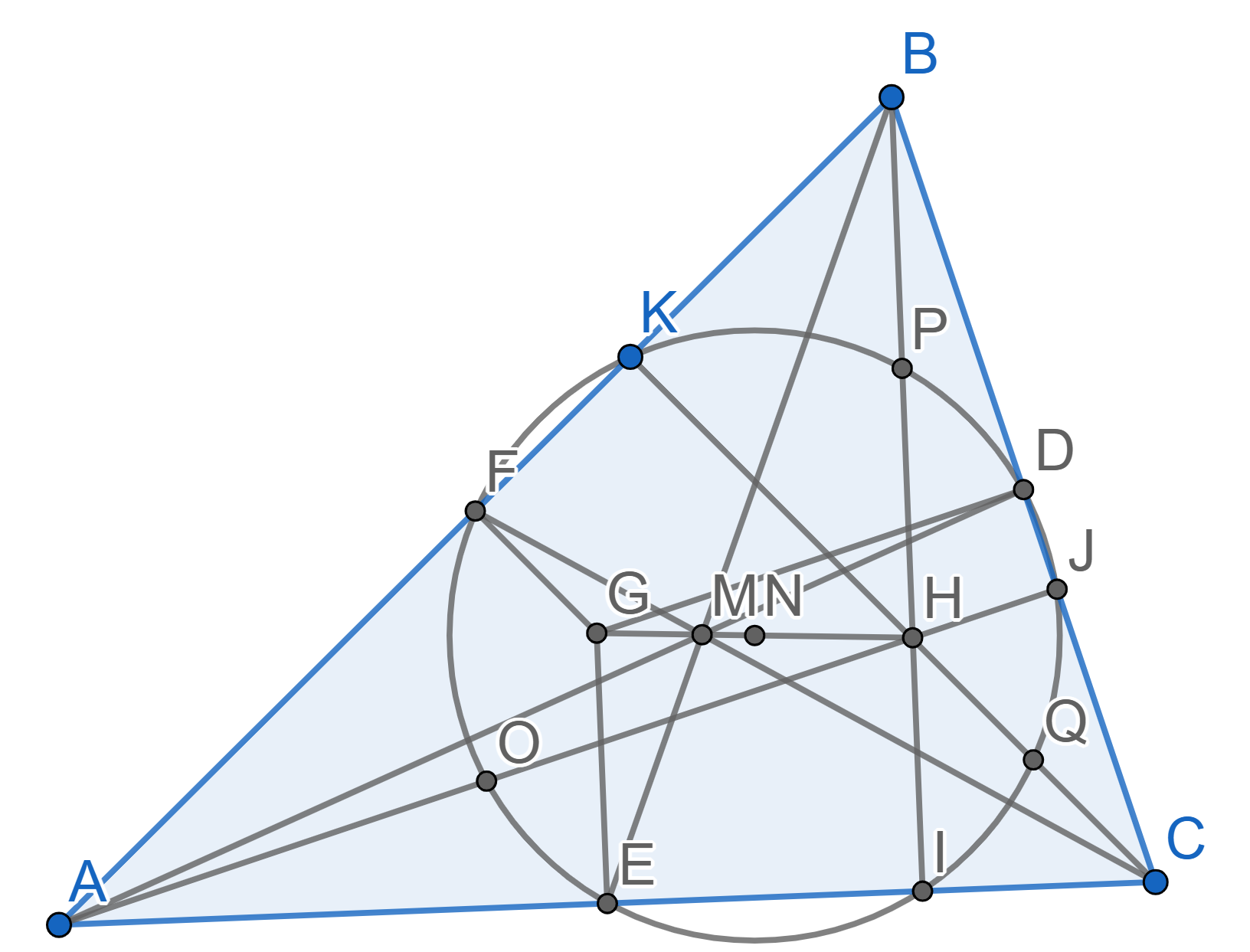
Let \(ABC\) be a triangle with midpoints \(D\) on the side \(BC\), \(E\) on the side \(AC\) and \(F\) on the side \(AB\). Let \(M\) be the point of intersection of all medians of the triangle \(ABC\) and let \(H\) be the point of intersection of the heights \(AJ\), \(BI\) and \(CK\). Consider the Euler circle of the triangle \(ABC\), which is the one that contains the points \(D,J,I,E,F,K\). This circle intersects the segments \(AH\), \(BH\) and \(CH\) at the points \(O\), \(P\) and \(Q\) respectively. Prove that \(O\), \(P\) and \(Q\) are the midpoints of the segments \(AH\), \(BH\) and \(CH\).
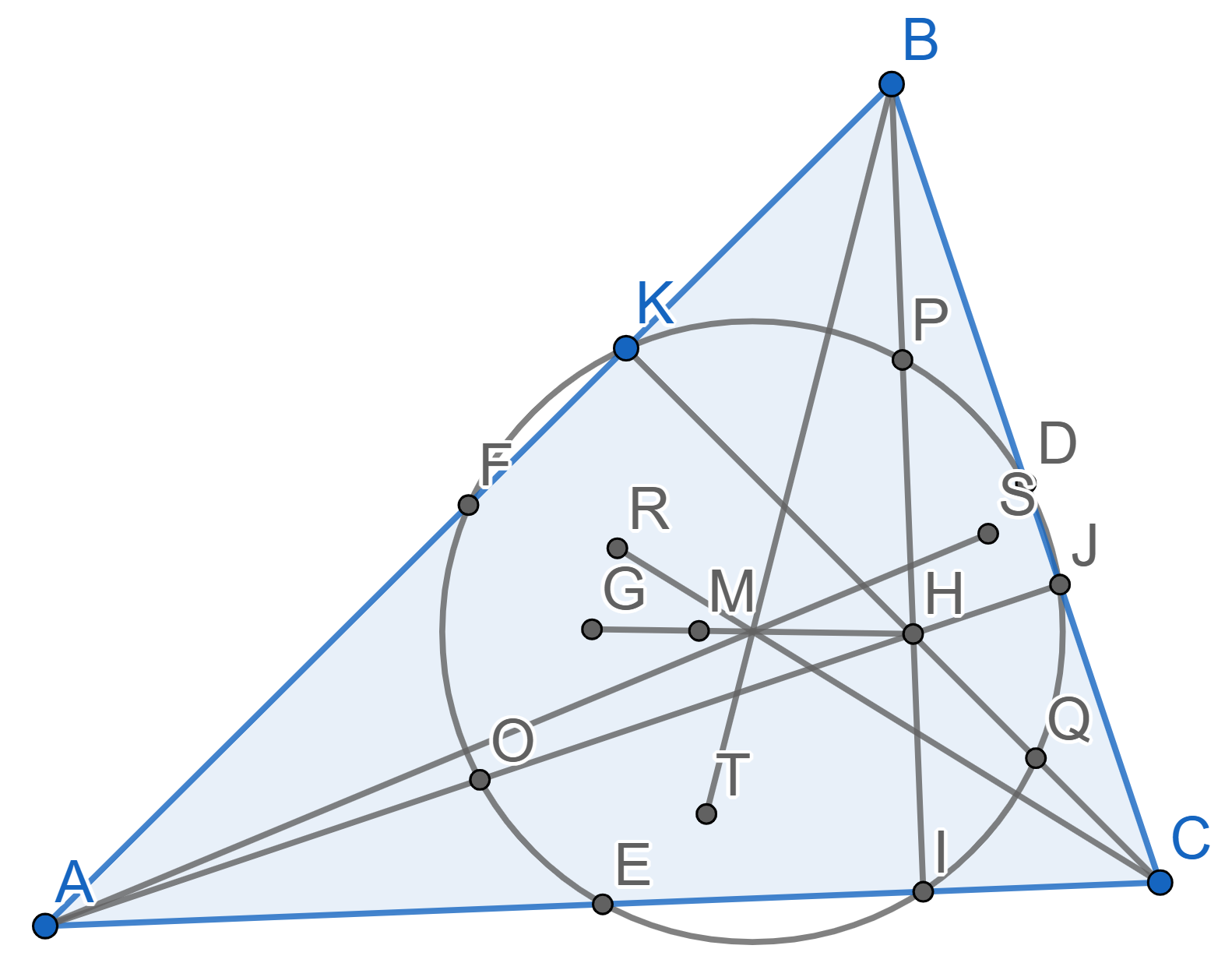
Consider the point \(H\) of intersection of the heights of the triangle \(ABC\). Prove that Euler lines of the triangles \(ABC\), \(ABH\), \(BCH\) and \(ACH\) intersect at one point. On the diagram below the points \(R,S,T\) are the points of intersection of medians in triangles \(ABH\), \(BCH\), and \(ACH\) respectively.
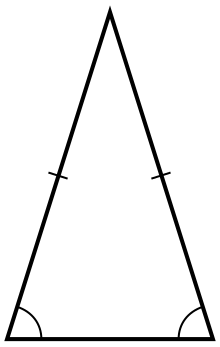
What are the symmetries of an isosceles triangle (which is not equilateral)?
What are the symmetries of the reduce-reuse-recycle symbol?

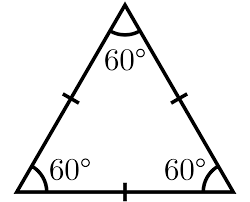
What are the symmetries of an equilateral triangle?
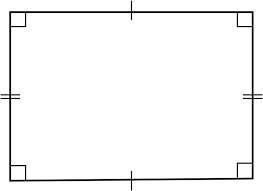
What are the symmetries of a rectangle (which is not a square)?
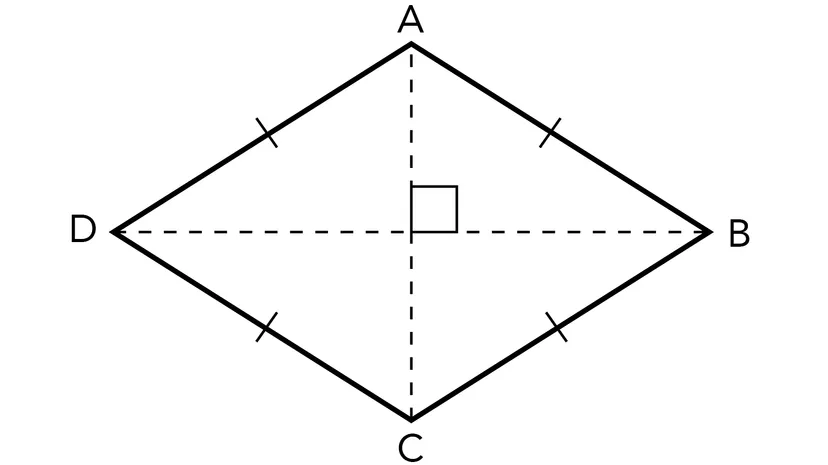
What are the symmetries of a rhombus (which isn’t a square)?
There are six symmetries of an equilateral triangle: three reflections, and three rotations (thinking of the identity as one the rotations). Label the three reflections \(s_1\), \(s_2\) and \(s_3\). Label the identity by \(e\), rotation by \(120^{\circ}\) as \(r_1\), and rotation by \(240^{\circ}\) clockwise as \(r_2\).
Note the following definition: Each symmetry has an inverse. Suppose we apply symmetry \(x\). Then there is some symmetry we can apply after \(x\), which means that overall, we’ve applied the identity. What are the inverses of \(r_1\) and \(s_1\)?