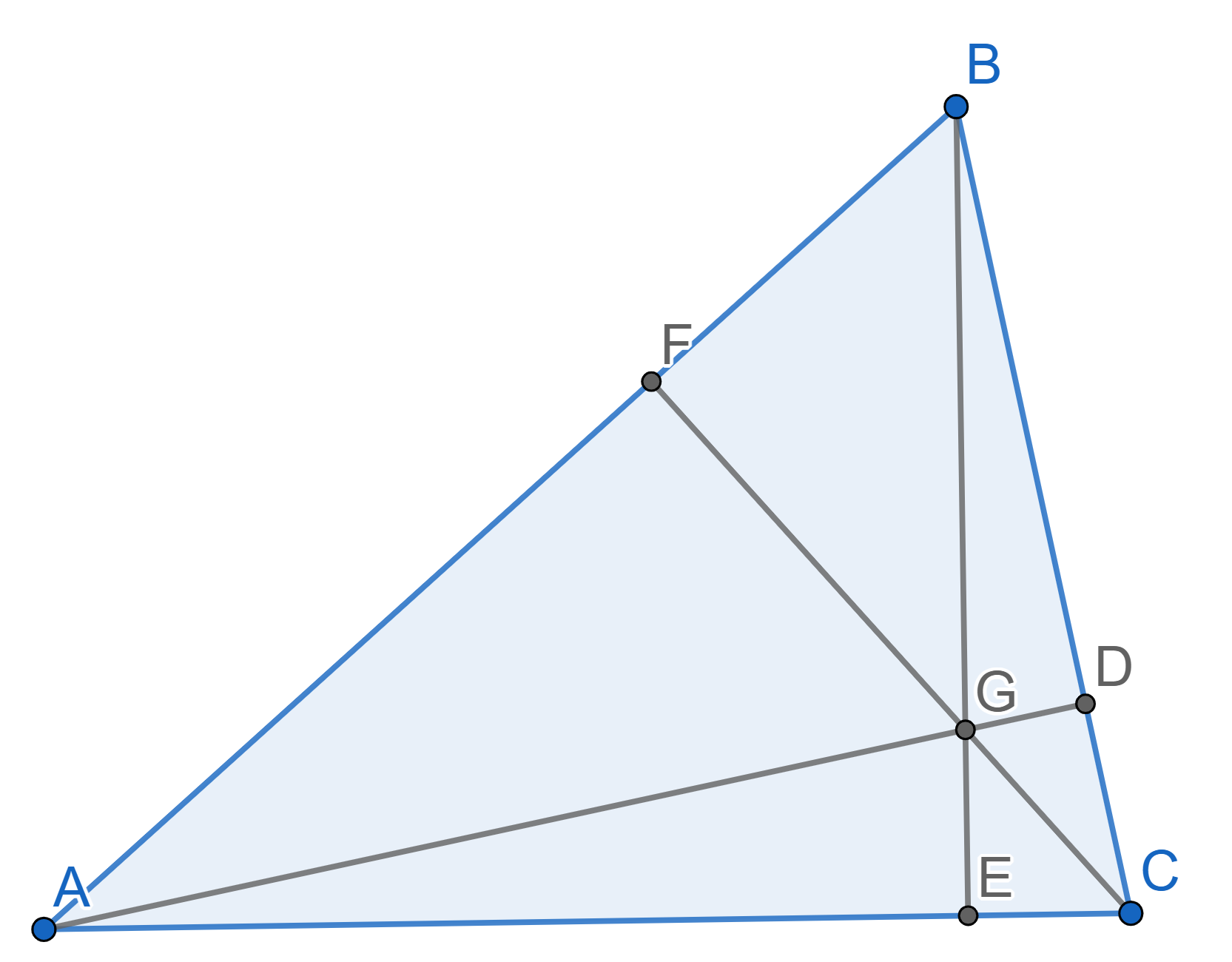
Problems

Rational numbers \(x,y,z\) are such that all the numbers \(x+y^2+z^2\), \(x^2+y+z^2\), \(x^2+y^2+z\) are integers. Prove that \(2x\) is also an integer.

A grasshopper can only make jumps exactly \(5\) inches in length. He wants to visit all \(8\) dots on the picture, where the length of the side of a unit square is one inch. Find the smallest number of jumps he will have to do if he can start and finish in any dot. It is allowed to use any point on the plane, not necessarily the ones on the picture.

The Tour de Clochemerle is not yet as big as the rival Tour de France. This year there were five riders, Arouet, Barthes, Camus, Diderot and Eluard, who took part in five stages. The winner of each stage got \(5\) points, the runner up \(4\) points and so on down to the last rider who got \(1\) point. The total number of points acquired over the five states was the rider’s score. Each rider obtained a different score overall and the riders finished the whole tour in alphabetical order with Arouet gaining a magnificent 24 points. Camus showed consistency by gaining the same position in four of the five stages and Eluard’s rather dismal performance was relieved by a third place in the fourth stage and first place in the final stage.

Where did Barthes come in the final stage?

Prove that the product of five consecutive integers is divisible by \(120\).

Prove that the vertices of a planar graph can be coloured in (at most) six different colours such that every pair of vertices joined by an edge are of different colours.

Note: a graph is planar if it can be drawn in the plane with no edges crossing. For example, three houses, each of which is connected to three utilities, is not a planar graph.
You may find it useful to use the Euler characteristic: a planar graph with \(v\) vertices, \(e\) edges and \(f\) faces satisfies \(v-e+f=2\).

Norman painted the plane using two colours: red and yellow. Both colours are used at least once. Show that no matter how Norman does this, there is a red point and a yellow point exactly \(1\)cm apart.

Two players are playing a game. The first player is thinking of a finite sequence of positive integers \(a_1\), \(a_2\), ..., \(a_n\). The second player can try to find the first player’s sequence by naming their own sequence \(b_1\), \(b_2\), ..., \(b_n\). After this, the first player will give the result \(a_1b_1 + a_2b_2 + ...+a_nb_n\). Then the second player can say another sequence \(c_1\), \(c_2\), ..., \(c_n\) to get another answer \(a_1c_1+ a_2c_2 + ... +a_nc_n\) from the first player. Find the smallest number of sequences the second player has to name to find out the sequence \(a_1\), \(a_2\), ..., \(a_n\).

The letters \(A\), \(R\), \(S\) and \(T\) represent different digits from \(1\) to \(9\). The same letters correspond to the same digits, while different letters correspond to different digits.
Find \(ART\), given that \(ARTS+STAR=10,T31\).

Let \(ABC\) be a non-isosceles triangle. The point \(G\) is the point of intersection of the medians \(AE\), \(BF\), \(CD\). The point \(H\) is the point of intersection of all heights. The point \(I\) is the center of the circumscribed circle of \(ABC\), or the point of intersection of all perpendicular bisectors to the segments \(AB\), \(BC\), \(AC\).
Prove that points \(I,G,H\) lie on one line and that the ratio \(IG:GH = 1:2\). The line that all of \(I\), \(G\) and \(H\) lie on is called the Euler line of triangle \(ABC\).

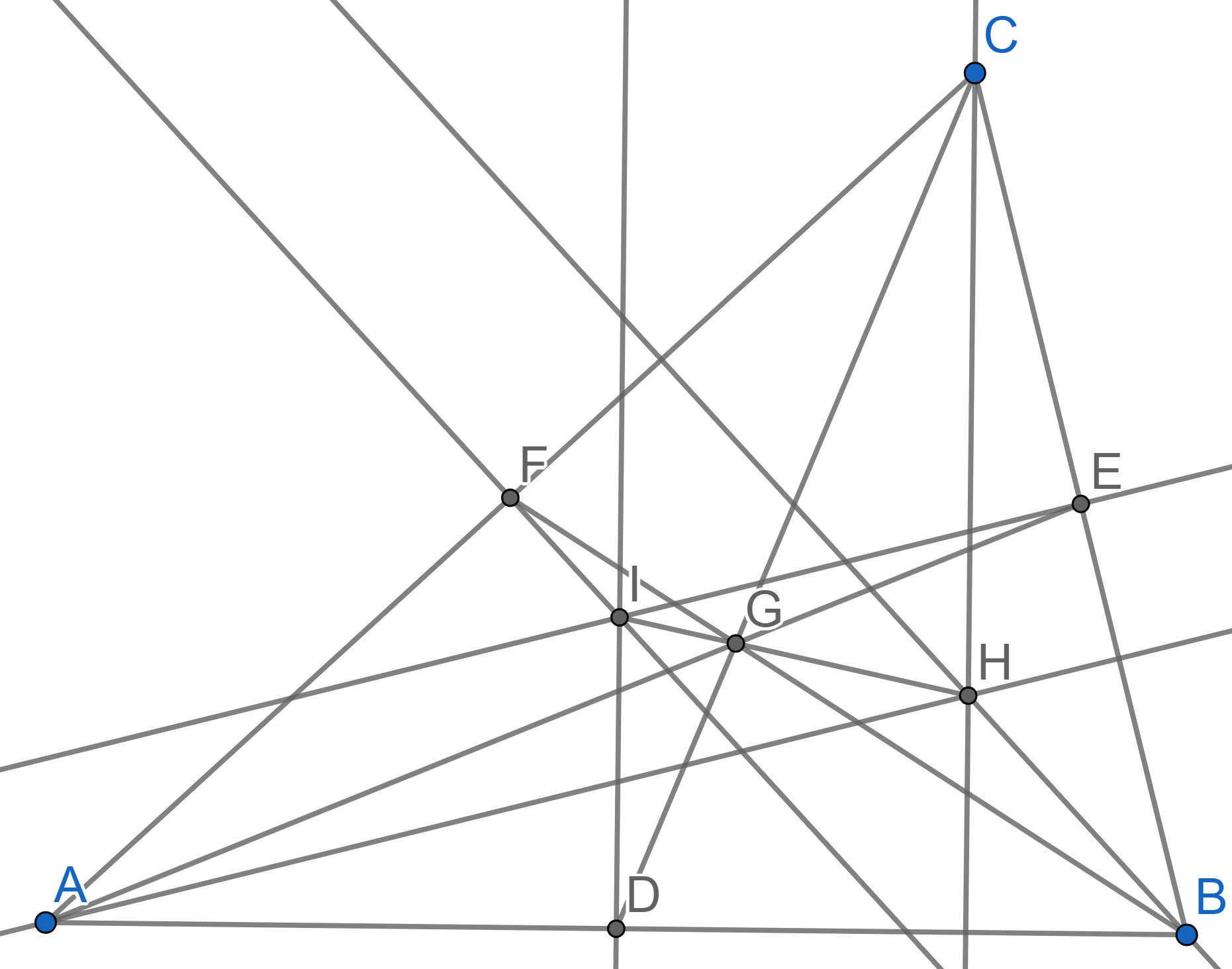
Paloma wrote digits from \(0\) to \(9\) in each of the \(9\) dots below, using each digit at most once. Since there are \(9\) dots and \(10\) digits, she must have missed one digit.

In the triangles, Paloma started writing either the three digits at the corners added together (the sum), or the three digits at the corners multiplied together (the product). She gave up before finishing the final two triangles.

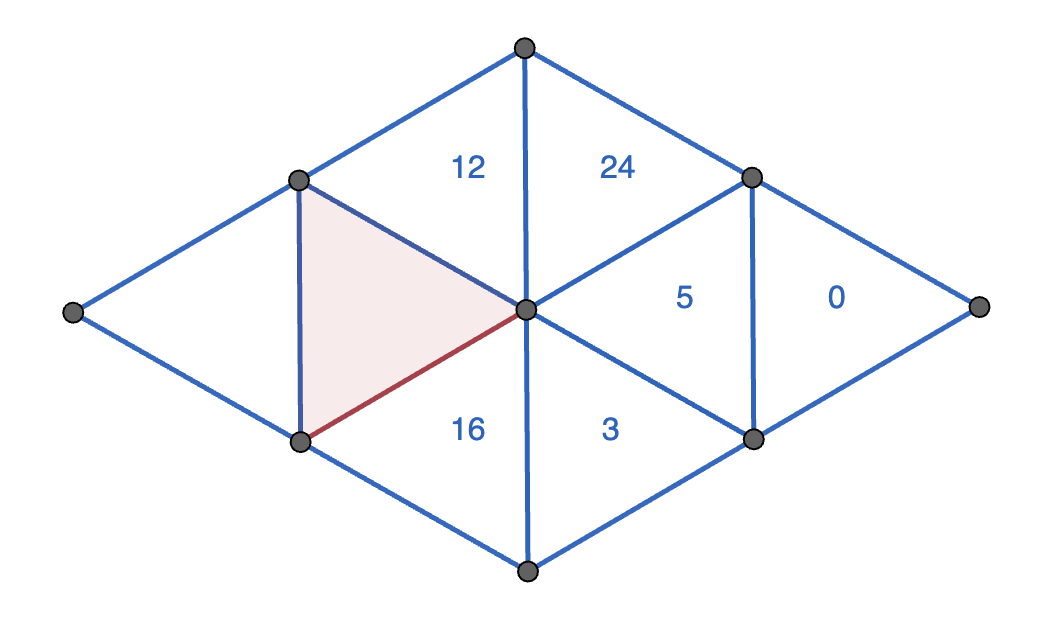
What numbers could Paloma have written in the interior of the red triangle? Demonstrate that you’ve found all of the possibilities.