Problems

\(x\), \(y\) and \(z\) are all integers. We’re told that \[\begin{align} x^3yz&=6\\ xy^3z&=24\\ xyz^3&=54. \end{align}\] What’s \(xyz\)?

In the diagram, all the small squares are of the same size. What fraction of the large square is shaded?

The letters \(O\), \(P\), \(S\) and \(T\) represent different digits from \(1\) to \(9\). The same letters correspond to the same digits, while different letters correspond to different digits.

Find \(O+P+S+T\), given that \(SPOT+POTS=15,279\).

A remainder is the number that is “left over" from division. Even if a number is not divisible by another number fully, we can still divide, but leaving a remainder. The remainder is less than the number we’re dividing by. For example, a remainder of \(44\) in division by \(7\) is \(2\), because \(44 = 6 \times 7 + 2\).

More generally, given any integer \(n\) and positive integer \(k\), we can always write \(n=qk+r\), where \(0\leq r<k\). We say that \(k\) goes into \(n\) \(q\) times, and a little bit (\(r\)) is left. If that little bit was larger than \(k\), it could “go into" \(n\) once more. This means we can always enforce the condition \(0\leq r<k\) on the remainder \(r\).

The general rule is that the remainder of a sum, difference or a product of two remainders is equal to the remainder of a sum, difference or a product of the original numbers. What that means is if we want to find a remainder of a product of two numbers, we need to look at the individual remainders, multiply them, and then take a remainder.

For example, \(10\) leaves the remainder \(3\) when divided by \(7\) and \(11\) leaves the remainder \(4\) when divided by \(7\). The product \(10\times11=110\) has the same remainder as the product of the individual remainders. We first multiply \(3\times4=12\) and then calculate the remainder upon division by \(7\), which is \(5\) because \(12=7+5\). That means that \(110\) gives a remainder of \(5\) when divided by \(7\). We can verify the result by calculating the remainder without simplifying first: \(110=15\times7+5\).

Here is a useful notation when discussing problems involving remainders and divisibility although it is not necessary for this problem sheet. Take two integers \(a\) and \(b\). If they differ by a multiple of a positive integer \(k\), then we write \(a \equiv b \pmod{k}\). For example, since \(24 - 10 = 2 \times 7\), we can express this fact by \(10 \equiv 24 \pmod{7}\). We say that 10 and 24 are congruent modulo 7.

Using this new notation, we can easily express the rules for remainders. Let \(a \equiv b \pmod{k}\) and \(c \equiv d \pmod{k}\). Then we have \(a + c \equiv b + d \pmod{k}\) and \(a \times c \equiv b \times d \pmod{k}\). As an example, again consider the calculation of the remainder of \(10 \times 11\) when divided by 7. We have \(10 \times 11 \equiv 3 \times 4 \equiv 12 \equiv 5 \pmod{7}\).

We make one last observation, which shows the utility of remainder when discussing divisibility. Saying that a number \(a\) is divisible by a number \(k\) is the same as saying the remainder of \(a\) when divided by \(k\) is 0. In congruence notation, the latter condition is \(a \equiv 0 \pmod{k}\).

Let’s have a look at some examples with remainders:

Picasso colours every point on the circumference of a circle red or blue. Is he guaranteed to create an equilateral triangle all of whose vertices are the same colour?

Let \(A\), \(B\), \(C\), \(D\), \(E\) be five different points on the circumference of a circle in that (cyclic) order. Let \(F\) be the intersection of chords \(BD\) and \(CE\). Show that if \(AB=AE=AF\) then lines \(AF\) and \(CD\) are perpendicular.

Let \(a\), \(b\) and \(c\) be positive real numbers such that \(a+b+c=3\). Prove that \(a^a+b^b+c^c\ge3\).

David and Esther play the following game. Initially, there are three piles, each containing 1000 stones. The players take turns to make a move, with David going first. Each move consists of choosing one of the piles available, removing the unchosen pile(s) from the game, and then dividing the chosen pile into 2 or 3 non-empty piles. A player loses the game if they are unable to make a move. Prove that Esther can always win the game, no matter how David plays.

Rational numbers \(x,y,z\) are such that all the numbers \(x+y^2+z^2\), \(x^2+y+z^2\), \(x^2+y^2+z\) are integers. Prove that \(2x\) is also an integer.

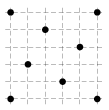
A grasshopper can only make jumps exactly \(5\) inches in length. He wants to visit all \(8\) dots on the picture, where the length of the side of a unit square is one inch. Find the smallest number of jumps he will have to do if he can start and finish in any dot. It is allowed to use any point on the plane, not necessarily the ones on the picture.