Problems
Prove that \(n^{n+1}>(n+1)^n\) for integers \(n\ge3\).
What is the following as a single fraction? \[\frac{1}{1\times2}+\frac{1}{2\times3}+\frac{1}{3\times4}+...+\frac{1}{98\times99}+\frac{1}{99\times100}.\]
Prove that \(3\) always divides \(2^{2n}-1\), where \(n\) is a positive integer.
Adi and Maxim play a game. There are \(100\) sweets in a bowl, and they each take in turns to take either \(2\), \(3\) or \(4\) sweets. Whoever cannot take any more sweets (since the bowl is empty, or there’s only \(1\) left) loses.
Maxim goes first - who has the winning strategy?
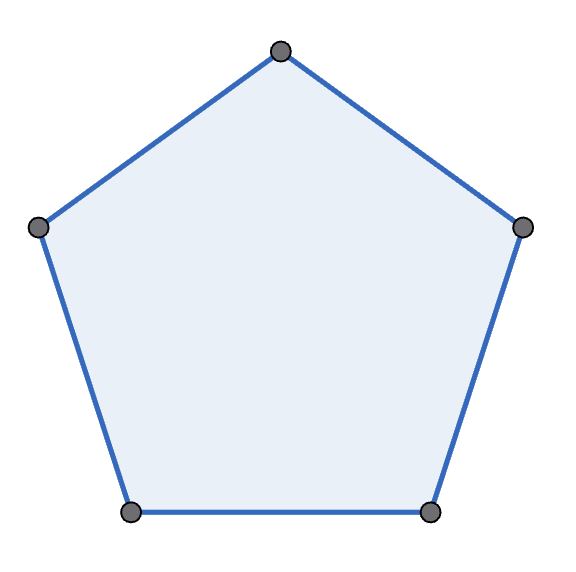
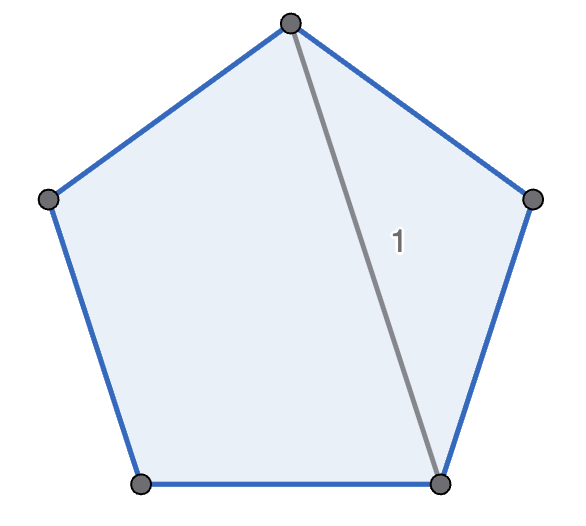
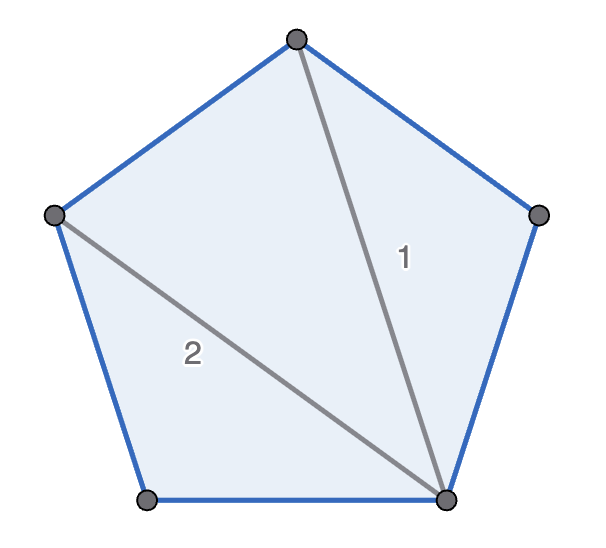
Michelle and Mondo play the following game, with Michelle going first. They start with a regular polygon, and take it in turns to move. A move is to pick two non-adjacent points in one polygon, connect them, and split that polygon into two new polygons. A player wins if their opponent cannot move - which happens if there are only triangles left. See the diagram below for an example game with a pentagon. Prove that Michelle has the winning strategy if they start with a decagon (\(10\)-sided polygon).
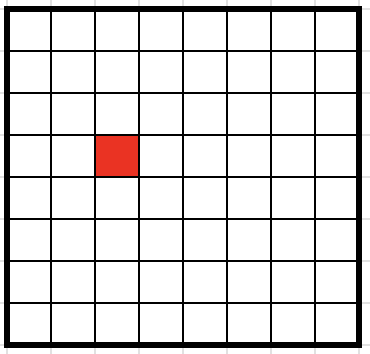
One square is coloured red at random on an \(8\times8\) grid. Show that no matter where this red square is, you can cover the remaining \(63\) squares with \(21\) ‘L’ triominoes, with no gaps or overlaps.

Let \(n\) be a positive integer. Show that \(1+3+3^2+...+3^{n-1}+3^n=\frac{3^{n+1}-1}{2}\).
Show that all integers greater than or equal to \(8\) can be written as a sum of some \(3\)s and \(5\)s. e.g. \(11=3+3+5\). Note that there’s no way to write \(7\) in such a way.
Determine all integer solutions to the equation \(24a + 16b = 6\).
John’s father is 28 years older than John and next year he will be exactly three times the age of John. How old is John’s father?