Problems
Prince Hattius tests his three wisest men with a hat puzzle. He tells them that he’ll put a hat on each of their heads, either green or yellow. These wise men, used to such puzzles, know that in such a setup they’ll be able to see the colours of the other two hats, but not their own.
Then the Prince says that at least one hat is green and the winner is the first person to work out the colour of his own hat. He adds on that this puzzle is fair to all of them - what happens?
This time three children with muddy faces run into the house. They are perfect logicians, but don’t yet know whether their own faces are muddy - yet they can see the other childrens’ faces.
Their dad says that at least one of them has a muddy face. And that he’ll keep repeating sentence every ten seconds until all children with muddy faces step forward.
Show that all three step forward after he’s said the sentence for the third time.
Three witches (Rosalind, Sabrina and Theresa) are having a duel between themselves. Rosalind is the most accurate, hitting her target \(100\%\) of the time. Sabrina is moderately accurate, hitting her target \(\frac{2}{3}\) of the time. Theresa still needs to practise, so only hits her target \(\frac{1}{3}\) of the time.
The witches take it in turns to fire shots. Once a witch has been shot, she can no longer fire shots. To make it fair given their respective accuracies, they agree that the order will be Theresa, Sabrina and Rosalind, and then repeat in that order until the end.
Why is Theresa’s best strategy to fire her first shot away from both of her opponents?
Anna gives three pupils at We Solve Problems (Jacob, Leonhard and Sophie) the following puzzle. She writes down three different numbers on pieces of card, and asks each of the three pupils to hold up their cards. She asks them to do this in such a way that they can’t see their own card, but that the other two people can see theirs.
Sophie sees that Jacob has \(8\) and
Leonhard has \(12\). Anna then tells
them that two of the cards add up to the third.
Sophie says ‘I don’t know my number.’
Leonhard says ‘I also don’t know my number.
What is Sophie’s number?
One of three friends gives the other two a puzzle. Mario says “I’ve thought of two different one-digit numbers. When you multiply these two numbers, the last digit of that is the same as the last digit of Lizzie’s house number. What’s the sum of these two one-digit numbers?"
Ioannis says “I don’t know Lizzie’s house number"
Then Lizzie says “Well, obviously I know my own house number. And now I’ve worked out the sum of the two numbers."
Finally Ioannis says “Ahh, I didn’t know the sum before, but now I
know the sum."
What’s the sum?
Princess Hattius invites several of the court’s Logicians to the forest. She tells them she’ll put a hat on each of their heads. The logicians will be able to see the colours of others’ hats, but not their own. The logicians are used to such puzzles, and so know that they’re not allowed to take off their own hat, or look in a mirror, or lake reflection. They are only allowed to work out their hat’s colour by logic and deduction.
The princess tells them she’ll ring a bell every minute, and that once a logician has worked out his or her own hat’s colour, then they should stand up and leave at the next bell. She also tells them that every colour appears twice, so each logician sees someone else with the same colour hat of their own.
What happens?
Michelle and Robbie ask Uri his age, while they’re all on a bus - instead of just answering them, Uri gives them a puzzle. Uri says that he has two younger brothers, and the product of all of our ages (in whole numbers) is \(144\).
Michelle replies that this is nowhere near enough information.
Then Uri says “Well, the sum of our ages is the bus number."
Robbie says “That narrows things down a bit, but I still don’t know how old you are."
Uri says “Oh I forgot to say! My brothers are twins."
Michelle and Robbie say “ we know." How old is Uri?
King Hattius has \(n\) prisoners, when \(n\ge4\) is a positive integer, and is feeling generous since his court of Logicians did well at his daughter’s logic puzzle. This means he offers the prisoners a puzzle, and he’ll let them all free if at least one of them is correct.
He has lots of hats, coming in \(n\) different colours. He tells the prisoners that he’ll put a hat on each of their heads. They might all have different coloured hats, or some of the hat’s colours could be the same. The king tells them that they can see everyone else’s hat colour, but not their own, and that they’re not allowed to communicate once their hats are on. They all have to simultaneously guess the colour of their hat.
He does give them the chance to come up with a strategy before he puts their hats on. How would you help the prisoners escape?
Pascal and Pierre are trying to work out Pythagoras. Being a bit obnoxious, Pythagoras puts a list of \(10\) possible dates on the table in front of them. In private, Pythag tells Pascal only the month of his birthday, and Pierre only the day of the month.
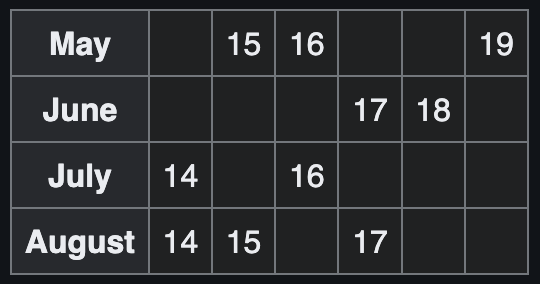
Pascal says “I don’t know Pythagoras’ birthday, but I also know that
Pierre doesn’t know."
Pierre then says “Pascal was right that I didn’t know, but now I do
know." Pascal replies “I know now Pythagoras’ birthday."
What is Pythagoras’ birthday?
Ignat gives two tutors a problem. He’s thinking of two different positive integers greater than \(1\), whose sum is at most \(100\). Ignat tells Pier (\(P\)) the product of the two numbers, and Sasha (\(S\)) the sum of the two numbers. Both Pier and Sasha know all of this, and then have a little conversation:
Sasha says that Pier doesn’t know the two numbers.
Pier says that he knows the two numbers.
Finally Sasha says that he knows the two numbers.
What are the two numbers?