Problems

Show that \(R(k,k)\ge2^{k/2}\).

Explain why you can’t rotate the sides on a normal Rubik’s cube to get to the following picture (with no removing stickers, painting, or other cheating allowed).

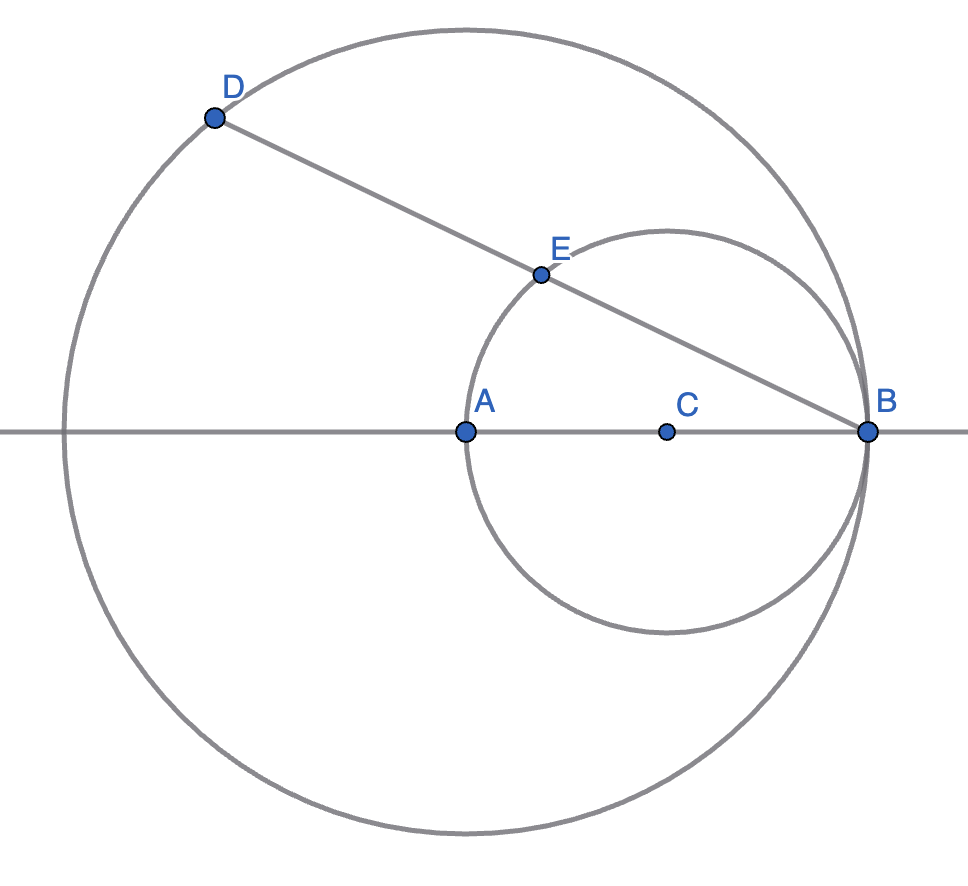
A circle with centre \(A\) has the point \(B\) on its circumference. A smaller circle is drawn inside this with \(AB\) as a diameter and \(C\) as its centre. A point \(D\) (which is not \(B\)) is chosen on the circumference of the bigger circle, and the line \(BD\) is drawn. \(E\) is the point where the line \(BD\) intersects the smaller circle.

Show that \(|BE|=|DE|\).

Are there any two-digit numbers which are the product of their digits?

The sum of Matt’s and Parker’s ages is \(63\) years. Matt is twice as old as Parker was when Matt was as old as Parker is now. How old are they? (Show that there’s no other ages that they could have)

How many \(10\)-digit numbers are there such that the sum of their digits is \(3\)?

We want to prove Monsky’s theorem as a corollary of Sperner’s lemma: it is not possible to dissect a square into an odd number of triangles of equal area. After scaling we can consider the square with coordinates: \((0,0),(0,1),(1,0),(1,1)\), which we want to cut into \(n\) triangles with area \(\frac{1}{n}\) each for an odd \(n\). Consider the following coloring of all the points with rational coordinates \((\frac{p}{q},\frac{r}{s})\) inside the square:
We look at the powers of \(2\) in the fractions \((\frac{p}{q},\frac{r}{s})\), first of all the numbers \(p,q\) are coprime, and thus only one of them is divisible by \(2\), same with \(r,s\). Then the following possibilities might occur:

1. Neither \(q\) nor \(s\) is divisible by \(2\). In this case we color the point red.

2. \(\frac{r}{s}\) is divisible by a larger or equal power of \(2\) than \(\frac{p}{q}\) and \(p\) is not divisible by \(2\). In this case we color the point blue.

3. \(\frac{p}{q}\) is divisible by a strictly larger power of \(2\) than \(\frac{r}{s}\) and \(r\) is not divisible by \(2\). In this case we color the point green.

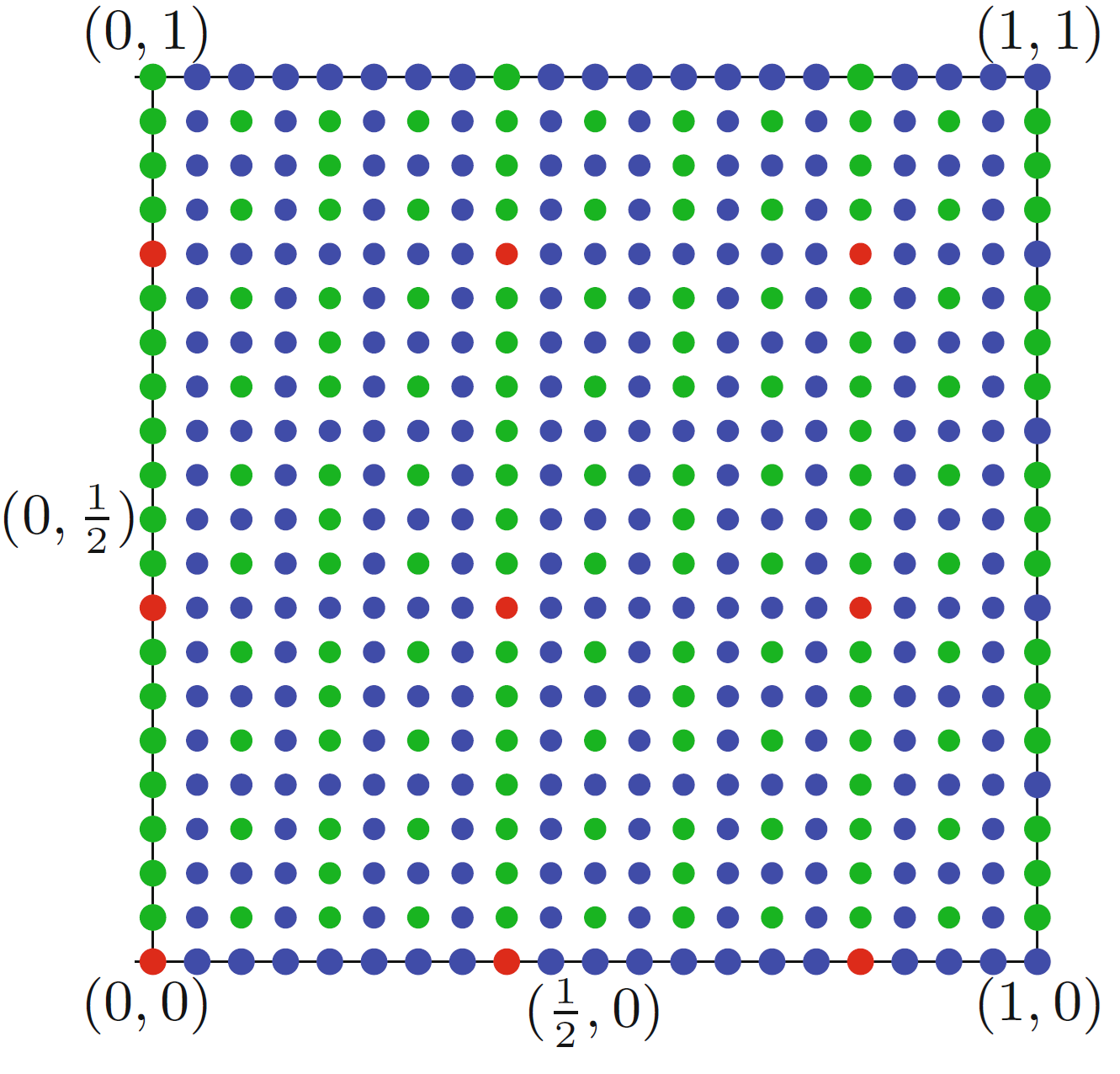
Under an assumption (which you do not have to prove) that the area of any rainbow triangle is at least \(\frac{1}{2}\) prove the Monsky’s theorem.

The sum of digits of a positive integer \(n\) is the same as the number of digits of \(n\). What are the possible products of the digits of \(n\)?

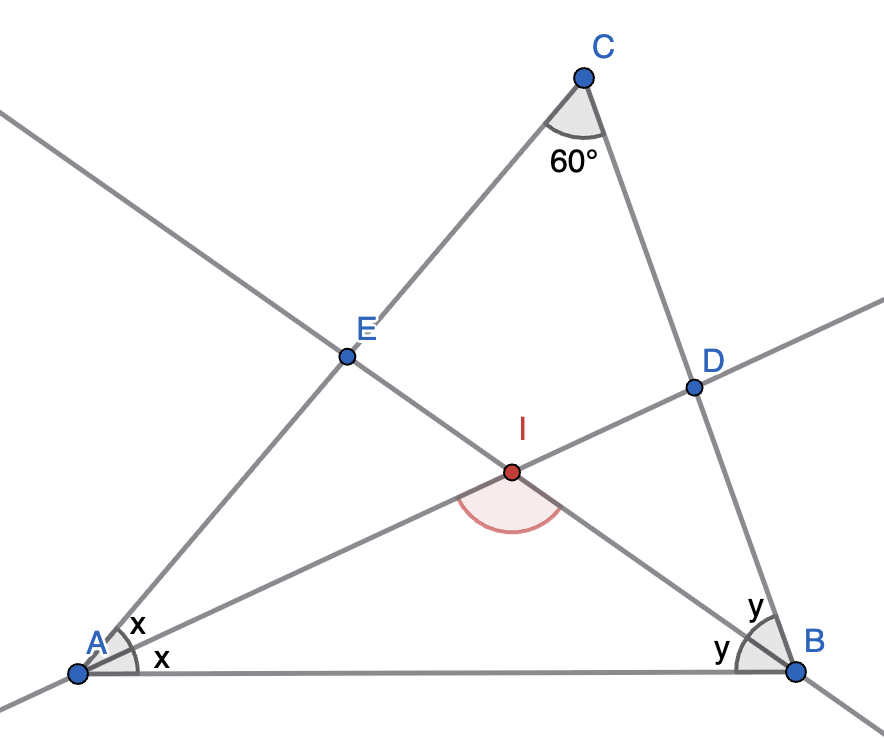
In the triangle \(\triangle ABC\), the angle \(\angle ACB=60^{\circ}\), marked at the top. The angle bisectors \(AD\) and \(BE\) intersect at the point \(I\).

Find the angle \(\angle AIB\), marked in red.

Find, with proof, all integer solutions of \(a^3+b^3=9\).