Problems
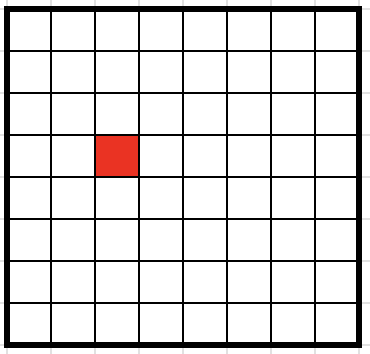
One square is coloured red at random on an \(8\times8\) grid. Show that no matter where this red square is, you can cover the remaining \(63\) squares with \(21\) ‘L’ triominoes, with no gaps or overlaps.

Let \(n\) be a positive integer. Show that \(1+3+3^2+...+3^{n-1}+3^n=\frac{3^{n+1}-1}{2}\).
Show that all integers greater than or equal to \(8\) can be written as a sum of some \(3\)s and \(5\)s. e.g. \(11=3+3+5\). Note that there’s no way to write \(7\) in such a way.
Determine all integer solutions to the equation \(24a + 16b = 6\).
John’s father is 28 years older than John and next year he will be exactly three times the age of John. How old is John’s father?
You have an hourglass that measures 8 minutes and an hourglass that measures 12 minutes. How can you measure exactly 44 minutes with them?
Joe has two kinds of weights: 15 grams and 50 grams. He has an infinite supply of each type. Can you help him find a combination that is exactly 310 grams?
You may have seen the first example (seen below) previously. Before we get to that, let’s introduce some notation. We write \(K_n\) for the complete graph on \(n\) vertices - that is, every possible edge is present.
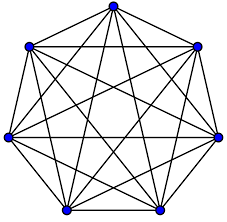
Note that edges don’t have a direction, and are between pairs of different vertices. Ramsey theory looks at what happens when we colour every edge in \(K_n\) either red or blue. Are we guaranteed a red \(K_3\) subgraph? No, because we could just colour every edge in \(K_n\) blue. Instead, we ask if we are guaranteed a red \(K_3\) or a blue \(K_3\) subgraph? It turns out yes, so long as \(n\) is big enough.
We can then look at extensions to this problem. We write \(R(s,t)\) for the least number \(n\) such that whenever you colour the edges of \(K_n\) in red or blue, then you’re guaranteed a red \(K_s\) or a blue \(K_t\). By least \(n\), this means that there’s a colouring of the edges of \(K_{n-1}\) with no red \(K_s\) or blue \(K_t\).
You may like to use the inequality \(R(m,n)\le R(m,n-1)+R(m-1,n)\). Furthermore, when both \(R(m,n-1)\) and \(R(m-1,n)\) are even, we have the stronger inequality of \(R(m,n)\le R(m,n-1)+R(m-1,n)-1\).
Find a formula for \(R(2,k)\), where \(k\) is a natural number.