Problems
George knows a representation of number “8” as the sum of its divisors in which only divisor “1” appears twice: \[8=4+2+1+1.\] His brother showed George that such representation exists for number “16” as well: \[16=8+4+2+1+1.\] He apologies for forgetting an example considering number “32” but he is sure once he saw such representation for this number.
(a) Help George to work out a suitable representation for number “32”;
(b) Can you think of a number which has such representation consisting of 7 terms?
(c) Of 11 terms?
(d) Can you find a number which can be represented as a sum of its divisors which are all different (pay attention that we don’t allow repeating digit “1” twice!)?
(e) What if we require this representation to consist of 11 terms?
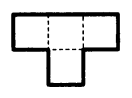
Two figures are said to be similar if they have “the same shape", that is: all corresponding angles are equal, and corresponding sides are in the same proportion. Using several copies of the figure below, construct a larger figure that is similar to it.
Divide a square into several triangles in such a way that every triangle shares a boundary with exactly three other triangles.
Jennifer draws a hexagon, and a line passing through two of its vertices. It turns out one of the figures in which the original hexagon is divided is a heptagon. Show an example of a hexagon and a line for which it is true.
There are four numbers written in a row. The first number is \(100\). It is known that if we divide the first number by the second number we will get a prime number as a result, if we the second number by the third number we will get a prime number, and if we divide the third number by the fourth number we will also get a prime number. Can all the resulting prime numbers be distinct?
George claims that he knows two numbers such that their quotient is equal to their product. Can we believe him? Prove him wrong or provide a suitable example.
Can Jennifer draw an octagon and a line passing through two of its vertices in such a way that this line cuts a 10-gon from it?
In the context of Example 14.2 what is the answer if we have five numbers instead of four? (i.e., can we get four distinct prime numbers then?)
Now George is sure he found two numbers with the quotient equal to their sum. And on top of that their product is still equal to the same value. Can it be true?
A maths teacher draws a number of circles on a piece of paper. When she shows this piece of paper to the young mathematician, he claims he can see only five circles. The maths teacher agrees. But when she shows the same piece of paper to another young mathematician, he says that there are exactly eight circles. The teacher confirms that this answer is also correct. How is that possible and how many circles did she originally draw on that piece of paper?