Problems
The three altitudes of a triangle intersect at a point called the orthocenter of the triangle. Suppose that the vertices of a \(\triangle ABC\) lie on a circle of radius 1 centered at 0. Show that the centroid, the orthocenter and the circumcenter of \(\triangle ABC\) are collinear. This line is called the Euler line of the triangle. Note that the circumcenter of \(\triangle ABC\) is just 0 by our assumption.
Now the detective has actually \(126\) people involved in the case! But he is in a big rush and needs to solve the case in only \(9\) days. Can you help him?
Without carrying out the multiplication, which number is larger \(1234567\times 1234569\) or \(1234568^2\)?
Which of the two fractions is larger? \[\frac{1\overbrace{00\cdots 00}^{1984\text{ zeroes}}1 }{1\underbrace{00\cdots 000}_{1985\text{ zeroes}}1}\qquad \text{or}\qquad \frac{1\overbrace{00\cdots 00}^{1985\text{ zeroes}}1 }{1\underbrace{00\cdots 000}_{1986\text{ zeroes}}1}\]
Which is larger? \[95^2+96^2\qquad \text{or}\qquad 2\times 95\times 96\]
Among all rectangles with perimeter \(4\), show that the one with largest area is a square, and determine that largest area.
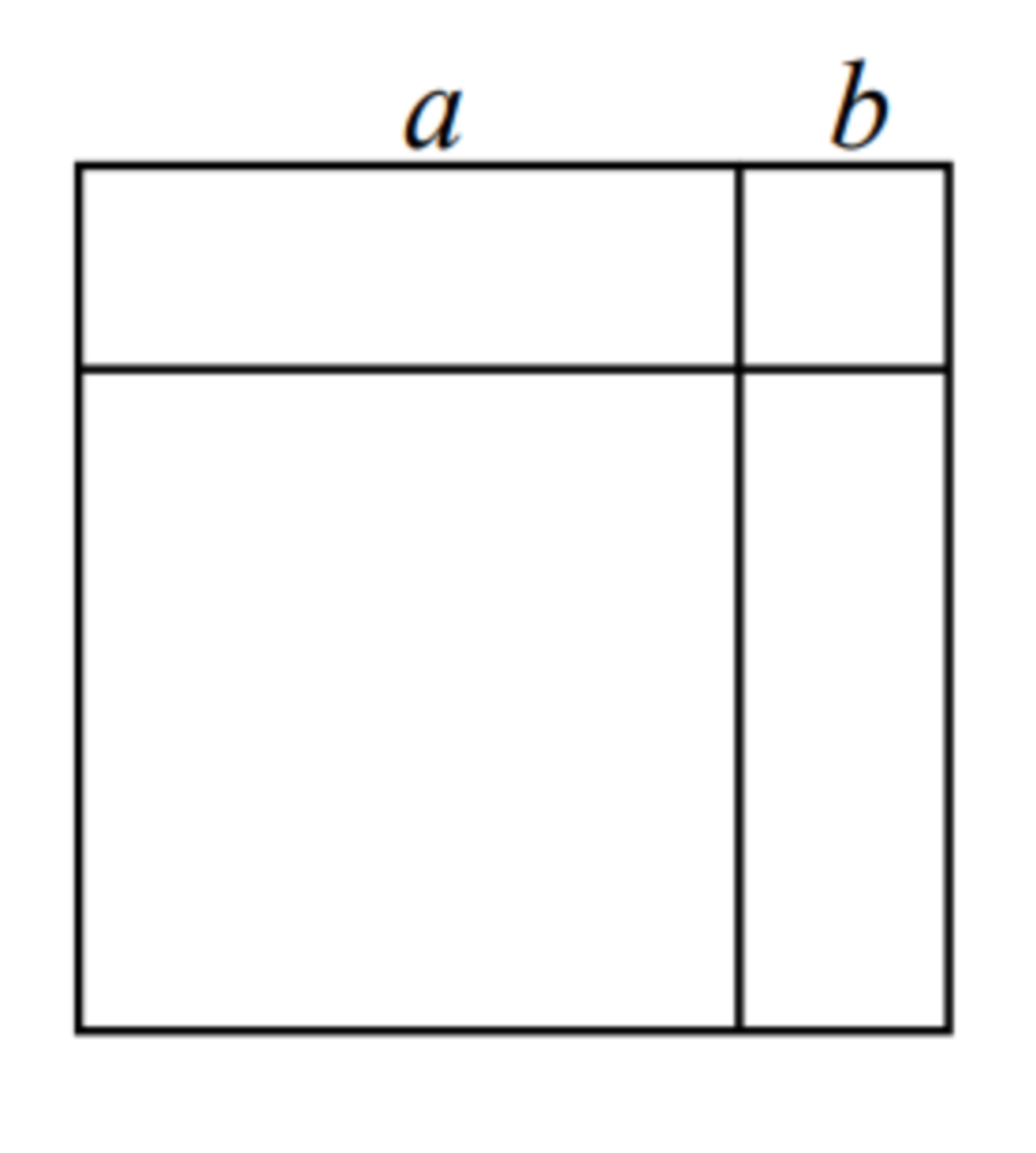
Show how the following diagram “proves" that \((a+b)^2=a^2+2ab+b^2\) without just expanding the brackets:
Show that the consecutive sum of odd numbers from \(1\) until any odd number is a perfect square. For example: \(1+3+5=3^2\), or \(1+3+5+7+9=5^2\).
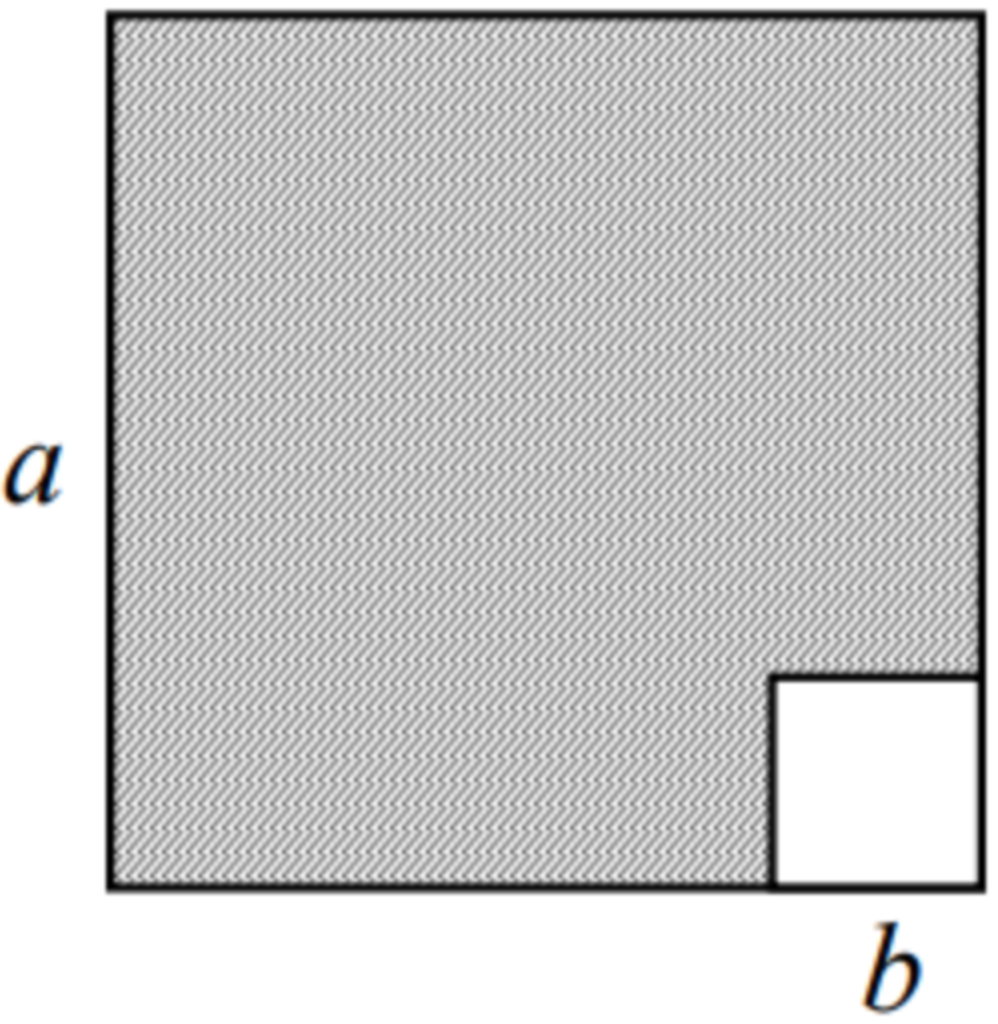
Explain how you can use the diagram below to show that \(a^2-b^2=(a+b)(a-b)\)