Problems
The Arithmetic-Geometric inequality is one of the most famous inequalities. It says that for positive numbers \(a\) and \(b\), \(\frac{a+b}2\geq \sqrt{ab}\). Show this inequality using the diagram below:
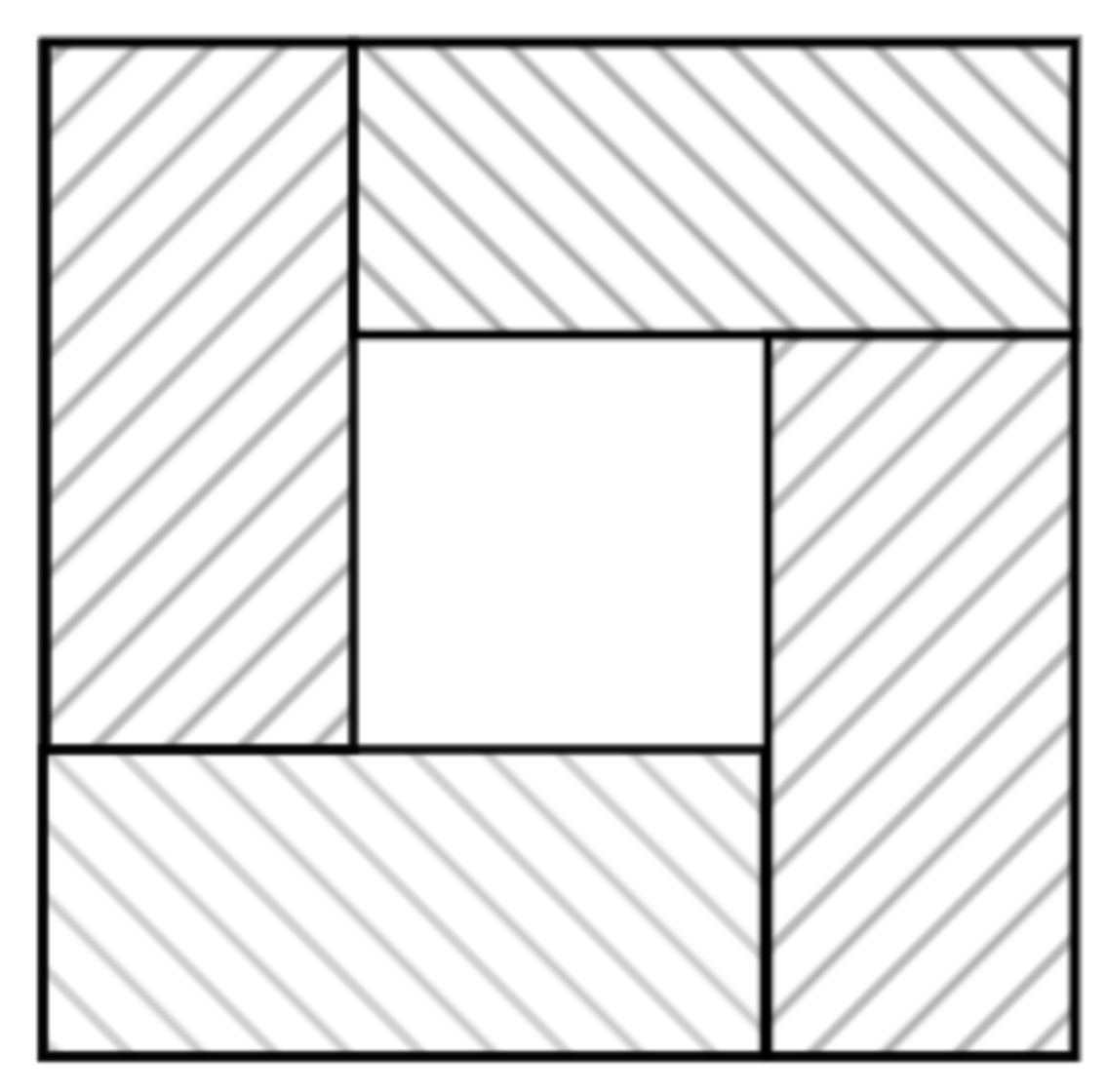
In the examples we showed that the sum of consecutive odd numbers starting from one was a perfect square. Now show how the following diagram can be used to give an alternative proof.
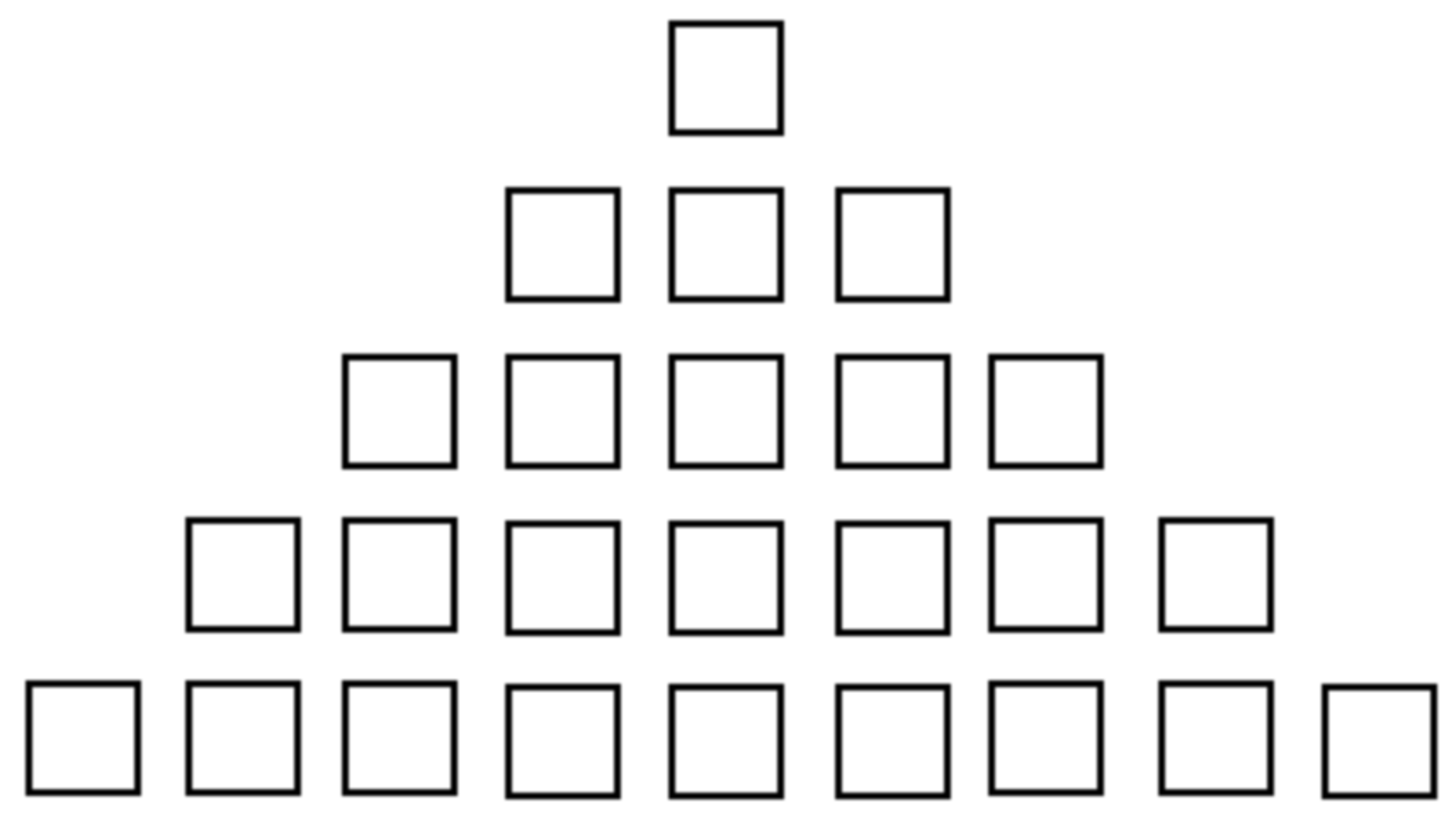
Using a visual proof, show that \(1^3+2^3+3^3+\cdots+n^3=\frac{1}{4}\left(n(n+1)\right)^2\)
Three clubs take part in a festival. Each club has at least one member.
During the festival, every member of one club shakes hands with every member of another club. In total (counting all three pairs of clubs), there were \(243\) handshakes between people from different clubs.
What is the smallest possible total number of participants?
Ten people take part in a challenge. Each is given a hat, either black or white. Everyone can see the other hats, but not their own.
They speak one at a time. On your turn, you must say black or white. One special person may instead say a whole number between \(0\) and \(777\), and then also guess their colour.
Before the hats are placed, the group may agree on a strategy of how to arrange themselves and what colours and numbers to say.
What is the largest number of people who can guarantee a correct guess?
What’s the smallest number of weights we need to weigh any number of grams from \(1\) to \(100\) in a balance scale, if your weights can be placed in any of the two plates of the scale?
Recall that when we write \(n!\) for some natural number \(n\), we mean \(1\times 2\times 3\times \cdots \times n\). You are given that \(20!=243290a0081766bc000,\) for some digits \(a,b,c\). Find those digits.
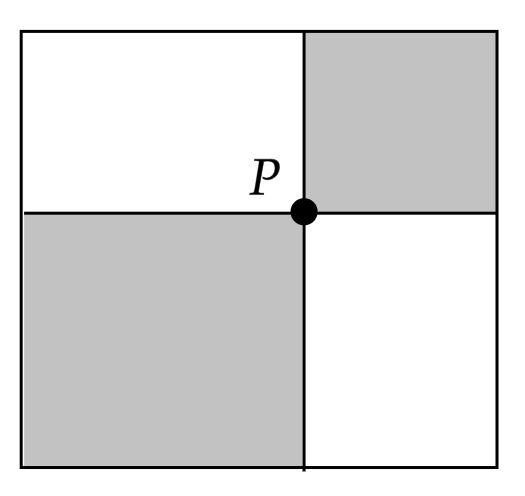
We have a square of side-length \(10\). A point \(P\) is drawn inside the square somewhere along the diagonal, and then the square is split and shaded as in the following diagram. Where should \(P\) be placed so that the shaded area is as smallest as possible? What will this shaded area be? You should provide a proof for your answer.
Let \(ABCD\) be a convex quadrilateral (convex means that all its internal angles are less than \(180^\circ\), i.e: it doesnt “bulge inwards"). Let \(E\) be the point of intersection of the diagonals. We are told that the triangles \(\triangle AED\) and \(\triangle BEC\) have equal areas. Show that \(AB\) and \(CD\) must be parallel.
For a natural number \(n\), we call the number \(1+2+3+\cdots + n\) the \(n^{\text{th}}\) triangular number, and we denote it by \(T_n\). Find \(T_n+T_{n-1}\) in terms of \(n\).