An \(8 \times 8\) chessboard has 30 diagonals total (15 in each direction). Is it possible to place several chess pieces on this chessboard in such a way that the total number of pieces on each diagonal would be odd?
Anna’s garden is a grid of \(n \times m\) squares. She wants to have trees in some of these squares, but she wants the total number of trees in each column and in each row to be an odd number (not necessarily the same, they just all need to be odd). Show that it is possible only if \(m\) and \(n\) are both even or both odd and calculate in how many different ways she can place the trees in the grid.
Matt built a simple wooden hut to protect himself from the rain. From the side the hut looks like a right triangle with the right angle at the top. The longer part of the roof has 20 ft and the shorter one has 15 ft. What is the height of the hut in feet?
The three sides of a right triangle have all integer lengths. Show that at least one of them has an even length.
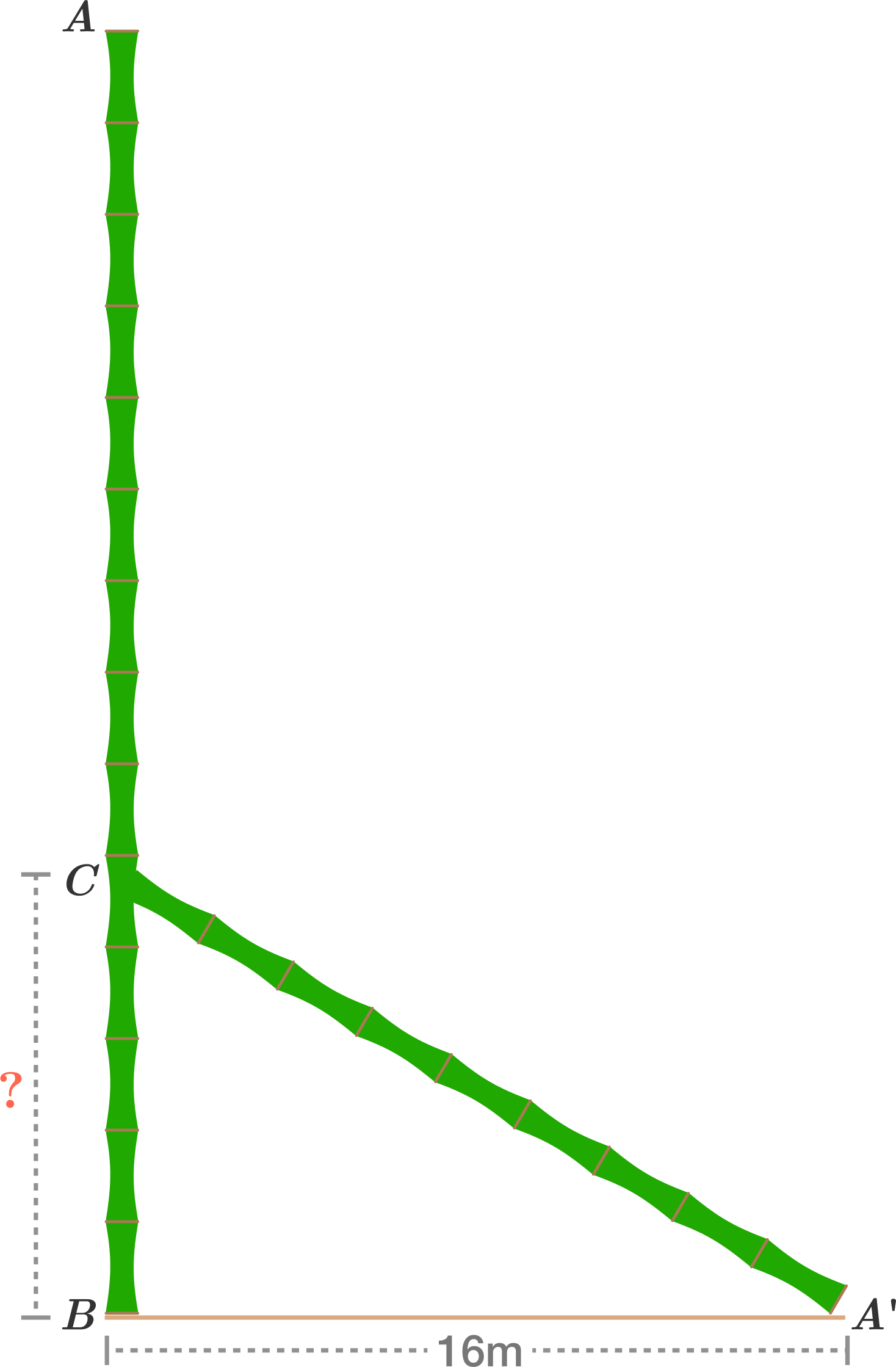
A bamboo tree, originally \(32\) metres high, broke in two parts. The end of the other one has fallen \(16\) metres far from the trunk. How high is the remaining vertical part of the bamboo tree?
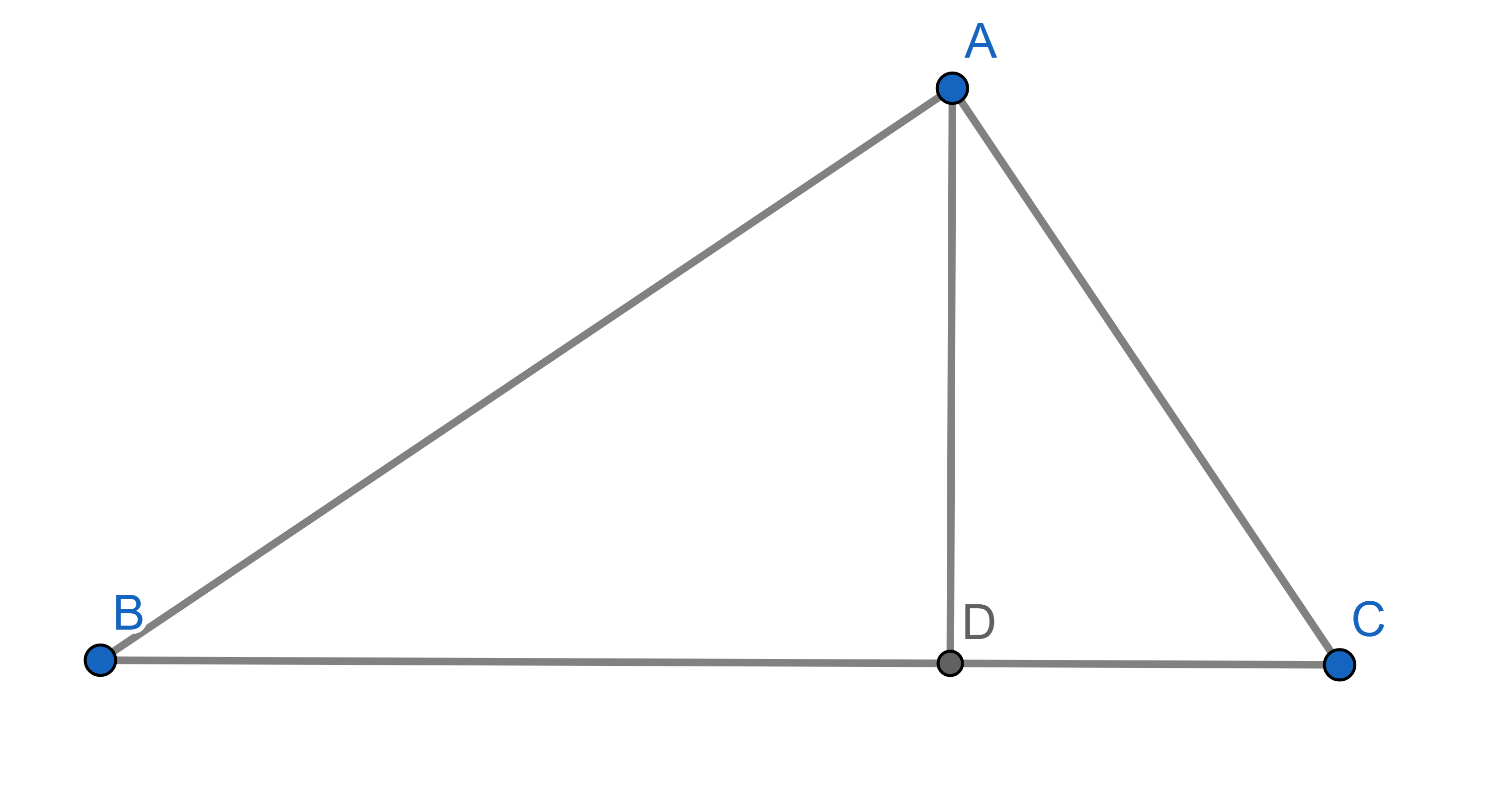
Matt has build an additional support for his hut (\(AD\)), whose length is equal to the height of the hut calculated in the Example 1. What are the distances from the base of the support to both ends of the hut? Looking at the picture, what are the distances \(BD\) and \(DC\), if \(AB = 20\) and \(AC = 15\)? Show that \(AD^2 = BD \times AC\) in this particular case. Do you think it is true in general?
Can you build a right triangle using 25 identical matches, without breaking them? You have to use them all. If yes, show how, if not, show why.
On the sides of a right triangle three equilateral triangles were built. Show that the areas of two of the two smaller ones sum up to the area of the larger one.
One triangle has sidelengths \(25,25\) and \(48\), the other triangle has sidelengths \(25,25\) and \(14\). Which of them has a larger area?
Find the area of the green annulus, if the marked pink segment has length \(1\).