Problems
Show that the equation \(x^2 +6x-1 = y^2\) has no solutions in integer \(x\) and \(y\).
Multiplication of numbers. Restore the following example of the multiplication of natural numbers if it is known that the sum of the digits of both factors is the same.
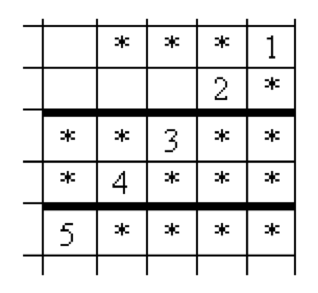
Restore the example of the multiplication.

Petya and Misha play such a game. Petya takes in each hand a coin: one – 10 pence, and the other – 15. After that, the contents of the left hand are multiplied by 4, 10, 12 or 26, and the contents of the right hand – by 7, 13, 21 or 35. Then Petya adds the two results and tells Misha the result. Can Misha, knowing this result, determine which hand – the right or left – contains the 10 pence coin?
Giuseppe has a sheet of plywood, measuring \(22 \times 15\). Giuseppe wants to cut out as many rectangular blocks of size \(3 \times 5\) as possible. How should he do it?
a) An apple is heavier than a banana, and a banana is heavier than a kiwi. What’s heavier – a kiwi or an apple?
b) A mandarin is lighter than a pear, and an orange is heavier than a mandarin. What is heavier – a pear or an orange?
The evil stepmother, leaving for the ball, gave Cinderella a bag in which rice and cous-cous were mixed, and ordered for them to be sorted. When Cinderella was leaving for the ball, she left three bags: one was rice, the other – cous-cous, and in the third – an unsorted mixture. In order not to confuse the bags, Cinderella attached to each of them a sign saying: “Rice”, “Cous-cous” and “Mixture”.
The stepmother returned from the ball first and deliberately swapped all the signs in such a way that on every sack there was an incorrect sign. The Fairy Godmother managed to warn Cinderella that now none of the signs on the bags are true. Then Cinderella took out only one single grain from one sack and, looking at it, immediately worked out what was in each bag. How did she do it?
Fred and George had two square cakes. Each twin made two straight cuts on his cake from edge to edge. However, one ended up with three pieces, and the other with four. How could this be?
There is a 12 litre barrel filled with water, and two empty barrels (one is 5 litres in volume and the other is 8 litres). Using these barrels, try to
a) divide the water into 2 parts with volumes: 3 litres and 9 litres;
b) divide the water into 2 parts with equal volume.
If yesterday was Thursday, what day will be yesterday for the day after tomorrow?