Problems

Let \(x\) be a 2 digit number. Let \(A\), \(B\) be the first (tens) and second (units) digits of \(x\), respectively. Suppose \(A\) is twice as large as \(B\). If we add the square of \(A\) to \(x\) then we get the square of a certain whole number. Find the value of \(x\).

The bank of the Nile was approached by a group of six people: three Bedouins, each with his wife. At the shore is a boat with oars, which can withstand only two people at a time. A Bedouin can not allow his wife to be without him whilst in the company of another man. Can the whole group cross to the other side?

Solve problem number 108736 for the inscription \(A\), \(BC\), \(DEF\), \(CGH\), \(CBE\), \(EKG\).

A row of 4 coins lies on the table. Some of the coins are real and some of them are fake (the ones which weigh less than the real ones). It is known that any real coin lies to the left of any false coin. How can you determine whether each of the coins on the table is real or fake, by weighing once using a balance scale?

Members of the State parliament formed factions in such a way that for any two factions \(A\) and \(B\) (not necessarily different)

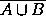
– also a faction (through

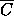
the set of all parliament members not included in \(C\) is denoted). Prove that for any two factions \(A\) and \(B\), \(A \cup % \includegraphics{https://problems-static.s3.amazonaws.com/production/problem_images/109909-3.png} B\) is also a faction.

Looking back at her diary, Natasha noticed that in the date 17/02/2008 the sum of the first four numbers are equal to the sum of the last four. When will this coincidence happen for the last time in 2008?

A magician with a blindfold gives a spectator five cards with the numbers from 1 to 5 written on them. The spectator hides two cards, and gives the other three to the assistant magician. The assistant indicates to the spectator two of them, and the spectator then calls out the numbers of these cards to the magician (in the order in which he wants). After that, the magician guesses the numbers of the cards hidden by the spectator. How can the magician and the assistant make sure that the trick always works?

In 10 boxes there are pencils (there are no empty boxes). It is known that in different boxes there is a different number of pencils, and in each box, all pencils are of different colors. Prove that from each box you can choose a pencil so that they will all be of different colors.

A block of cheese comes in packaging with parallel lines of different colours printed on it. If you cut along the red lines then you will get 5 slices of cheese, if you cut along the yellow lines then there will be 7 slices, and along the green lines you will get 11 slices. How many slices will you get if you cut along the lines of all three colours?

In Neverland, only elves and gnomes live. Gnomes lie about their gold, but in any other instances they tell the truth. Elves lie when talking about gnomes, but in other instances they tell the truth. One day two neverlandians said:

\(A\): All my gold I stole from the Dragon.

\(B\): You’re lying.

Determine whether each of them is an elf or a gnome.