We solve problems

In two purses lie two coins, and one purse has twice as many coins as the other. How can this be?

Problems Discrete Mathematics Algorithm Theory Theory of algorithms (other)

Three people A, B, C counted a bunch of balls of four colors (see table).

Each of them correctly distinguished some two colors, and confused the numbers of the other two colours: one mixed up the red and orange, another – orange and yellow, and the third – yellow and green. The results of their calculations are given in the table.

How many balls of each colour actually were there?

Problem #PRU-103812

Problems Number Theory Arithmetic operations. Number identities Discrete Mathematics Set theory and logic Mathematical logic Puzzles

11–11 2.0

Alex laid out an example of an addition of numbers from cards with numbers on them and then swapped two cards. As you can see, the equality has been violated. Which cards did Alex rearrange?

Problem #PRU-103815

Problems Discrete Mathematics Combinatorics Dissections, partitions, covers and tilings Dissections with certain properties Fun Problems Word Problems Tables and tournaments Tables and tournaments (other)

11–11 2.0

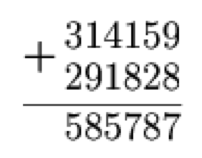
Cut the board shown in the figure into four congruent parts so that each of them contains three shaded cells. Where the shaded cells are placed in each part need not be the same.

Problem #PRU-103817

Problems Discrete Mathematics Algorithm Theory Theory of algorithms (other)

10–12 2.0

A family went to the bridge at night. The dad can cross over it in 1 minute, the mom can cross it in 2, the child takes 5 minutes, and grandmother in 10 minutes. They have one flashlight. The bridge can only withstands two people at a time. How can they all cross the bridge in 17 minutes? (If two people pass, then they go at the lower of their speeds.) You can not move along a bridge without a flashlight. You can not shine it from a distance.

Problem #PRU-103818

Problems Geometry Plane geometry Quadrilateral Parallelogram Special cases Rectangles and squares. Criteria and properties

11–12 2.0

Which rectangles with whole sides are there more of: with perimeter of 1996 or with perimeter of 1998? (The rectangles \(a \times b\) and \(b \times a\) are assumed to be the same).

Problem #PRU-103824

Problems Geometry Solid geometry Spheres Circle on a sphere Visual geometry in space

11–13 2.0

A globe has 17 parallels and 24 meridians. How many parts is the globe’s surface divided into? The meridian is an arc connecting the North Pole with the South Pole. A parallel is a circle parallel to the equator (the equator is also a parallel).

Problem #PRU-103825

Problems Algebra and arithmetic Arithmetics. Mental maths Methods Examples and counterexamples. Constructive proofs Discrete Mathematics Algorithm Theory Theory of algorithms (other)

10–12 2.0

Three hedgehogs divided three pieces of cheese of mass of 5g, 8g and 11g. The fox began to help them. It can cut off and eat 1 gram of cheese from any two pieces at the same time. Can the fox leave the hedgehogs equal pieces of cheese?

Problem #PRU-103827

Problems Dissections

11–11 2.0

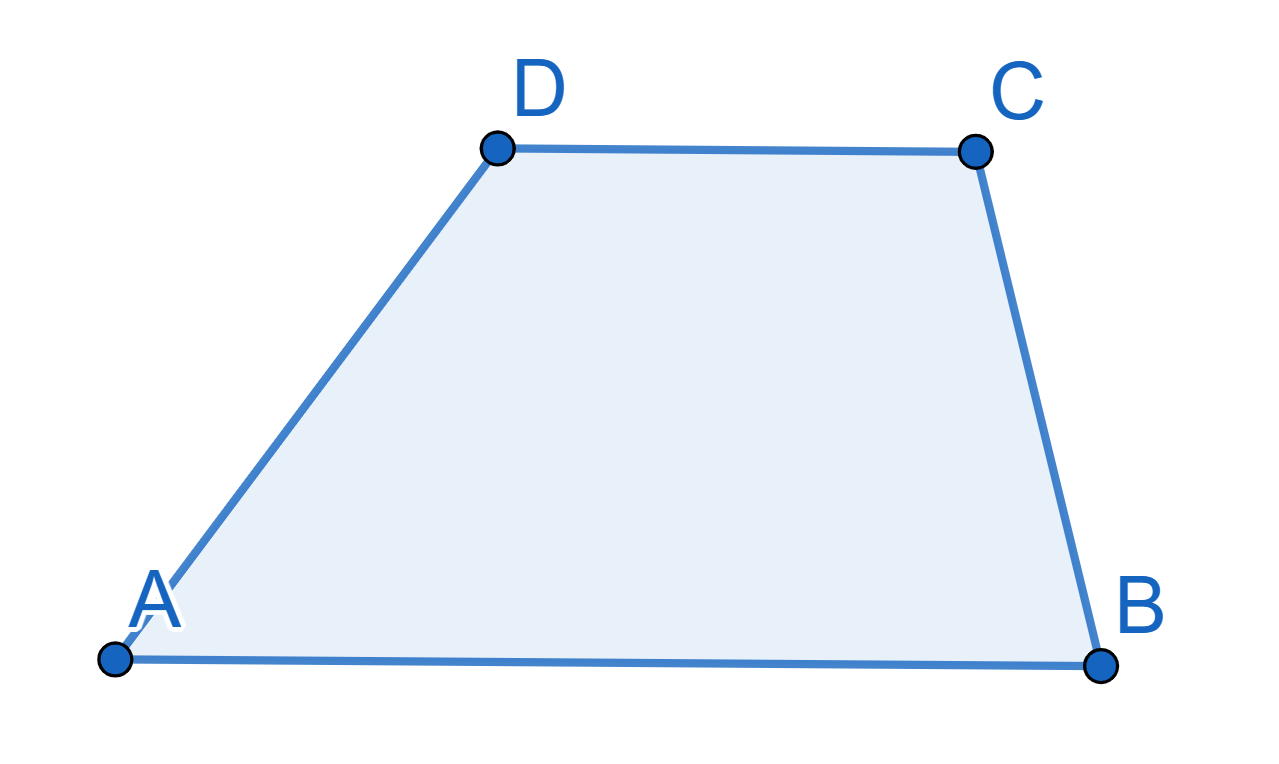
Cut the trapezium \(ABCD\) into two parts which you can use to construct a triangle.

Problem #PRU-103833

Problems Discrete Mathematics Algorithm Theory Theory of algorithms (other)

10–12 2.0

On the island of Contrast, both knights and liars live. Knights always tell the truth, liars always lie. Some residents said that the island has an even number of knights, and the rest said that the island has an odd number of liars. Can the number of inhabitants of the island be odd?