Problems
Find the largest value of the expression \(a + b + c + d - ab - bc - cd - da\), if each of the numbers \(a\), \(b\), \(c\) and \(d\) belongs to the interval \([0, 1]\).
To a certain number, we add the sum of its digits and the answer we get is 2014. Give an example of such a number.
It is known that \(AA + A = XYZ\). What is the last digit of the product: \(B \times C \times D \times D \times C \times E \times F \times G\) (where different letters denote different digits, identical letters denote identical digits)?
The pupils of class 5A had a total of 2015 pencils. One of them lost a box with five pencils, and instead bought a box with 50 pencils. How many pencils do the pupils of class 5A now have?
In one box, there are two pies with mushrooms, in another box there are two with cherries and in the third one, there is one with mushrooms and one with cherries. The pies look and weigh the same, so it’s not known what is in each one. The grandson needs to take one pie to school. The grandmother wants to give him a pie with cherries, but she is confused herself and can only determine the filling by breaking the pie, but the grandson does not want a broken pie, he wants a whole one.
a) Show that the grandmother can act so that the probability of giving the grandson a whole pie with cherries will be equal to \(2/3\).
b) Is there a strategy in which the probability of giving the grandson a whole pie with cherries is higher than \(2/3\)?
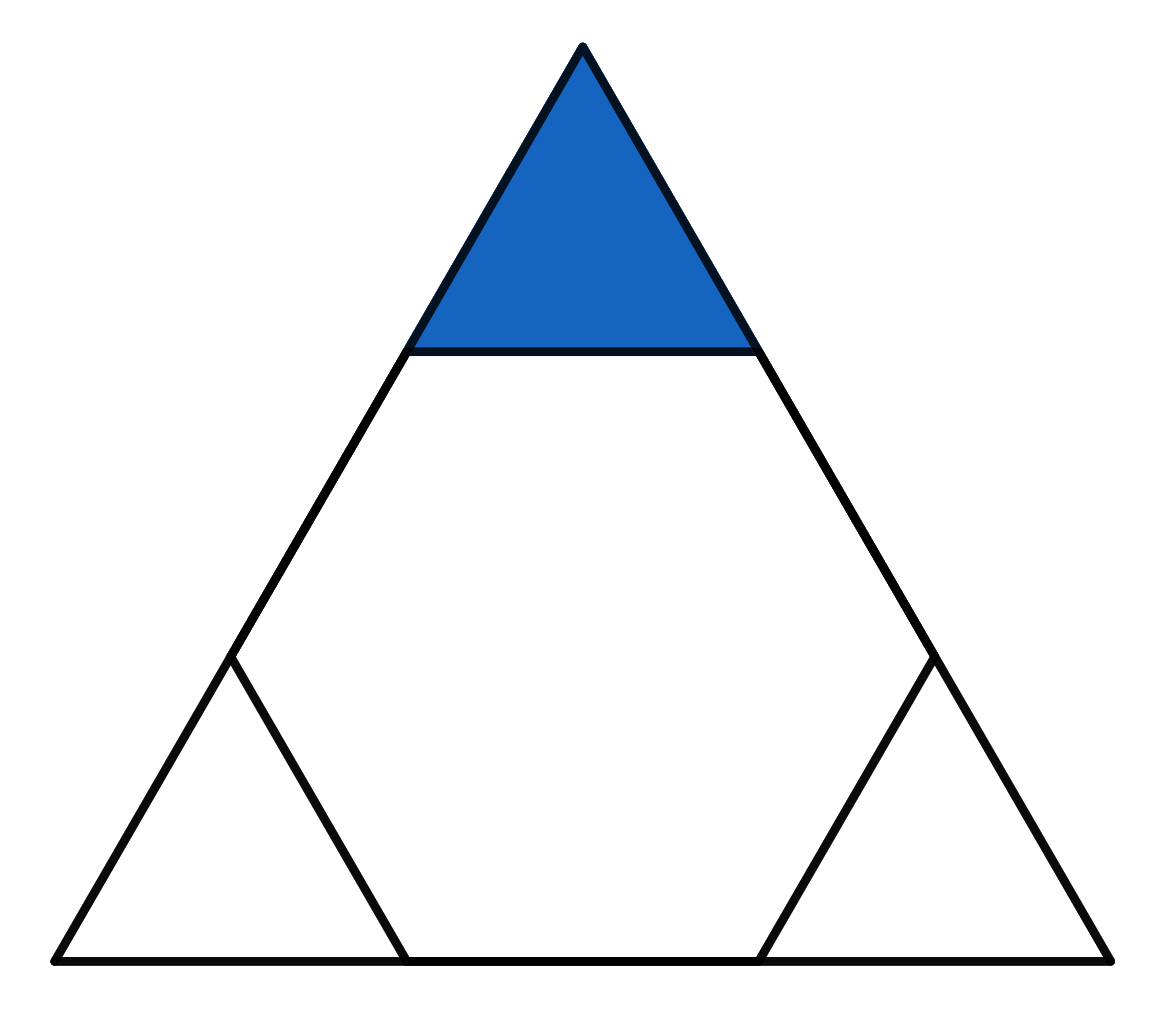
The triangle visible in the picture is equilateral. The hexagon inside is a regular hexagon. If the area of the whole big triangle is \(18\), find the area of the small blue triangle.
The White Rook pursues a black horse on a board of \(3 \times 1969\) cells (they walk in turn according to the usual rules). How should the rook play in order to take the horse? White makes the first move.
In a set there are 100 weights, each two of which differ in mass by no more than 20 g. Prove that these weights can be put on two cups of weighing scales, 50 pieces on each one, so that one cup of weights is lighter than the other by no more than 20 g.
Peter bought an automatic machine at the store, which for 5 pence multiplies any number entered into it by 3, and for 2 pence adds 4 to any number. Peter wants, starting with a unit that can be entered free of charge to get the number 1981 on the machine number whilst spending the smallest amount of money. How much will the calculations cost him? What happens if he wants to get the number 1982?
Izzy wrote a correct equality on the board: \(35 + 10 - 41 = 42 + 12 - 50\), and then subtracted 4 from both parts: \(35 + 10 - 45 = 42 + 12 - 54\). She noticed that on the left hand side of the equation all of the numbers are divisible by 5, and on the right hand side by 6. Then she took 5 outside of the brackets on the left hand side and 6 on the right hand side and got \(5(7 + 2 - 9)4 = 6(7 + 2 - 9)\). Having simplified both sides by a common multiplier, Izzy found that \(5 = 6\). Where did she go wrong?