Problems
One term a school ran 20 sessions of an after-school Astronomy Club. Exactly five pupils attended each session and no two students encountered one another over all of the sessions more than once. Prove that no fewer than 20 pupils attended the Astronomy Club at some point during the term.
In the rebus below, replace the letters with numbers such that the same numbers are represented with the same letter. The asterisks can be replaced with any numbers such that the equations hold.
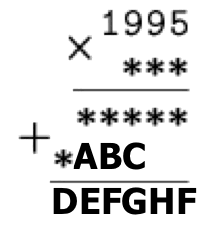
An explanation of the notation used: the unknown numbers in the third and fourth rows are the results of multiplying 1995 by each digit of the number in the second row, respectively. These third and fourth rows are added together to get the total result of the multiplication \(1995 \times ***\), which is the number in the fifth row. This is an example of a “long multiplication table”.
In two purses lie two coins, and one purse has twice as many coins as the other. How can this be?
Which five-digit numbers are there more of: ones that are not divisible by 5 or those with neither the first nor the second digit on the left being a five?
Three people A, B, C counted a bunch of balls of four colors (see table).
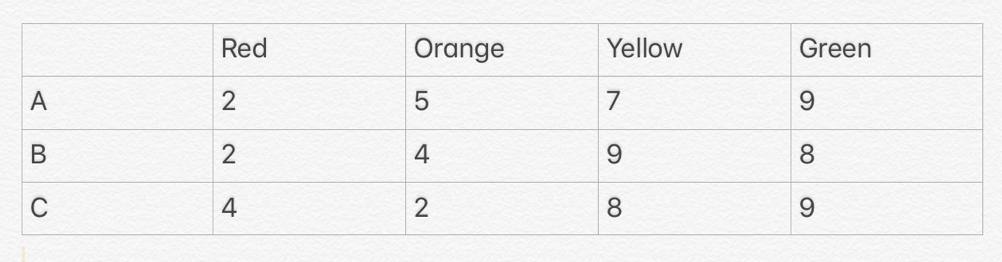
Each of them correctly distinguished some two colors, and confused the numbers of the other two colours: one mixed up the red and orange, another – orange and yellow, and the third – yellow and green. The results of their calculations are given in the table.
How many balls of each colour actually were there?
Alex laid out an example of an addition of numbers from cards with numbers on them and then swapped two cards. As you can see, the equality has been violated. Which cards did Alex rearrange?
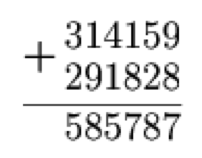
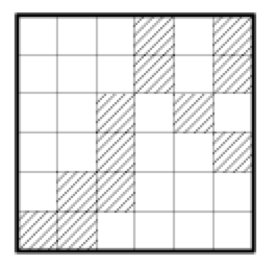
Cut the board shown in the figure into four congruent parts so that
each of them contains three shaded cells. Where the shaded cells are
placed in each part need not be the same.
A family went to the bridge at night. The dad can cross over it in 1 minute, the mom can cross it in 2, the child takes 5 minutes, and grandmother in 10 minutes. They have one flashlight. The bridge can only withstands two people at a time. How can they all cross the bridge in 17 minutes? (If two people pass, then they go at the lower of their speeds.) You can not move along a bridge without a flashlight. You can not shine it from a distance.
Which rectangles with whole sides are there more of: with perimeter of 1996 or with perimeter of 1998? (The rectangles \(a \times b\) and \(b \times a\) are assumed to be the same).
In Mexico, environmentalists have succeeded in enacting a law whereby every car should not be driven at least one day a week (the owner informs the police about their car registration number and the day of the week when this car will not be driven). In a certain family, all adults want to travel daily (each for their own business!). How many cars (at least) should the family have, if the family has a) 5 adults? b) 8 adults?