We solve problems

Problems Methods Algebraic methods Proof by exhaustion Set theory and logic Mathematical logic Puzzles

Find the smallest four-digit number \(CEEM\) for which there exists a solution to the rebus \(MN + PORG = CEEM\). (The same letters correspond to the same numbers, different – different.)

Problem #PRU-103883

Problems Set theory and logic Mathematical logic Mathematical logic (other)

11–12 2.0

A space traveller decided to visit the planet and upon arrival he met three inhabitants. The traveller asked each of the inhabitants: “How many truth tellers are there among your companions?”. The first one answered: “None.” The second one said: “One”. What did the third alien say?

Problem #PRU-103884

Problems Combinatorics Dissections, partitions, covers and tilings Dissections with certain properties Methods Examples and counterexamples. Constructive proofs Algebra and arithmetic Fractions Simple fractions

11–12 2.0

A rectangle is cut into several smaller rectangles, the perimeter of each of which is an integer number of meters. Is it true that the perimeter of the original rectangle is also an integer number of meters?

Problem #PRU-103885

Problems Combinatorics Partitions Tilings with ordinary and domino tiles

11–12 2.0

At the disposal of a tile layer there are 10 identical tiles, each of which consists of 4 squares and has the shape of the letter L (all tiles are oriented the same way). Can he make a rectangle with a size of \(5 \times 8\)? (The tiles can be rotated, but you cannot turn them over). For example, the figure shows the wrong solution: the shaded tile is incorrectly oriented.

Problem #PRU-103887

Problems Set theory and logic Mathematical logic Puzzles Algebra and arithmetic Fractions Simple fractions

12–12 2.0

Arrange brackets and arithmetic signs around these numbers so that the correct equality is obtained: \[\frac{1}{2}\quad \frac{1}{6}\quad \frac{1}{6009} \ = \ 2003.\]

Problem #PRU-103888

Problems Methods Algebraic methods Proof by exhaustion Geometry Solid geometry Visual geometry in space

11–12 2.0

A square napkin was folded in half, the resulting rectangle was then folded in half again (see the figure). The resulting square was then cut with scissors (in a straight line). Could the napkin have been broken up a) into 2 parts? b) into 3 parts? c) into 4 parts? d) into 5 parts? If yes – illustrate such a cut, if not – write the word “no”.

Problem #PRU-103899

Problems Combinatorics Discrete geometry

12–12 2.0

A rabbit, preparing for the arrival of guests, hung lightbulbs in three corners of his polygonal hole. Winnie the Pooh and Piglet came and noticed that lights did not illuminate all the pots of honey which were in the rabbit hole. When they reached for some honey, two of the lightbulbs broke. The rabbit moved the remaining light bulb into some corner so that the whole hole was lit up. Is this possible? (If yes, draw an example, if not, justify the answer.)

Problem #PRU-103946

Problems Algebra and arithmetic Arithmetic operations. Number identities

11–12 2.0

The number \(A\) is positive, \(B\) is negative, and \(C\) is zero. What is the sign of the number \(AB + AC + BC\)?

Problem #PRU-103947

Problems Geometry Plane geometry Area

10–12 2.0

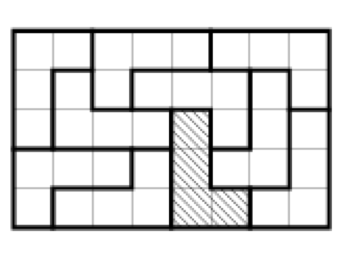
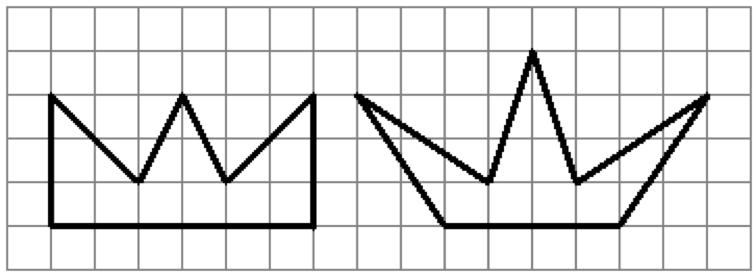
Find the area of the figures shown below.

Problem #PRU-103955

Problems Set theory and logic Algorithm Theory Game Theory Winning and loosing positions

12–13 2.0

Ben and Joe play chess. In addition to a chessboard, they have one rook, which they put in the lower right corner, and they move it in turns. It can only be moved upwards or to the left (for any number of cells). The player who can not make a move, loses. Joe goes first. Who will win with the correct method?