We solve problems

Find the area of the figures shown below.

Problems Discrete Mathematics Algorithm Theory Game theory Winning and loosing positions

Ben and Joe play chess. In addition to a chessboard, they have one rook, which they put in the lower right corner, and they move it in turns. It can only be moved upwards or to the left (for any number of cells). The player who can not make a move, loses. Joe goes first. Who will win with the correct method?

Problem #PRU-103960

Problems Methods Pigeonhole principle Pigeonhole principle (other)

11–13 2.0

Prove that if 21 people collected 200 nuts between them, there are two people in the group who collected the same number of nuts.

Problem #PRU-103964

Problems Number Theory Divisibility Division with remainders. Arithmetic of remainders Arithmetic of remainders Methods Pigeonhole principle Pigeonhole principle (other)

12–14 3.0

There are \(n\) integers. Prove that among them either there are several numbers whose sum is divisible by \(n\) or there is one number divisible by \(n\) itself.

Problem #PRU-103966

Problems Algebra Algebraic equations and systems of equations Higher order equations. Palindromic polynomial equations Equations of higher order (other) Calculus Real numbers Integer and fractional parts. Archimedean property

12–14 2.0

In Mongolia there are in circulation coins of 3 and 5 tugriks. An entrance ticket to the central park costs 4 tugriks. One day before the opening of the park, a line of 200 visitors queued up in front of the ticket booth. Each of them, as well as the cashier, has exactly 22 tugriks. Prove that all of the visitors will be able to buy a ticket in the order of the queue.

Problem #PRU-103967

Problems Discrete Mathematics Algorithm Theory Theory of algorithms (other)

10–12 2.0

There is a rectangular table. Two players start in turn to place on it one pound coin each, so that these coins do not overlap one another. The player who cannot make a move loses. Who will win with the correct strategy?

Problem #PRU-103969

Problems Discrete Mathematics Algorithm Theory Theory of algorithms (other)

10–12 2.0

a) Two players play in the following game: on the table there are 7 two pound coins and 7 one pound coins. In a turn it is allowed to take coins worth no more than three pounds. The one who takes the last coin wins. Who will win with the correct strategy?

b) The same question, if there are 12 one pound and 12 two pound coins.

Problem #PRU-103987

Problems Methods Pigeonhole principle Pigeonhole principle (other)

10–12 2.0

a) Prove that in any football team there are two players who were born on the same day of the week.

b) Prove that in the population of London, which is almost 9 million, there will be ten thousand people who celebrate their birthday on the same day.

Problem #PRU-104001

Problems Discrete Mathematics Combinatorics Dissections, partitions, covers and tilings Various dissection problems

12–13 2.0

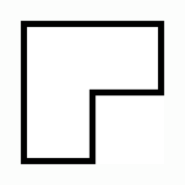
Kai has a piece of ice in the shape of a “corner” (see the figure). The Snow Queen demanded that Kai cut it into four equal parts. How can he do this?

Problem #PRU-104009

Problems Discrete Mathematics Set theory and logic Mathematical logic Mathematical logic (other)

12–13 2.0

The king made a test for the future groom of his daughter. He put the princess in one of three rooms, a tiger in the other, and left the last room empty. It is known that the sign on the door where the princess is sitting is true, where the tiger is – it is false, and nothing is known about the sign on the third room. The tablets are as follows:

1 – room 3 is empty

2 – the tiger is in room 1

3 – this room is empty

Can the prince correctly guess the room with the princess?