Problems

Find all rectangles that can be cut into \(13\) equal squares.

Cut a square into two equal:
1. Triangles.
2. Pentagons
3. Hexagons.

Today we will practice to encrypt and decipher information using some of the most common codes. Majority of the codes in use can be alphabetic and numeric, namely one may want to encode a word, a phrase, or a number, or just any string of symbols using either letters, or numbers, or both. Some of the codes, however may use various other symbols to encrypt the information. To solve some of the problems you will need the correspondence between alphabet letters and numbers
0.85

@*26c@ A & B & C & D &E & F &G &H &I &J &K &L &M&N&O&P&Q&R&S&T&U&V&W&X&Y&Z
1 & 2 & 3&4&5&6&7&8&9&10&11&12&13&14&15&16&17&18&19&20&21&22&23&24&25&26

Two expressions are written on the board:

\[1 + 22 + 333 + 4444 + 55555 + 666666 +7777777 + 88888888 + 999999999\] \[9 + 98 + 987 + 9876 + 98765 + 987654 + 9876543 + 98765432 + 987654321\]

Determine which one is greater or whether the numbers are equal.

Cut the "biscuit" into 16 congruent pieces. The sections are not necessarily rectilinear.

Bryn calls the date beautiful if all \(6\) digits of the date entry are different. For example: 19.04.23 is a beautiful date, but 19.02.23 and 01.06.23 are not. How many beautiful dates are there in \(2023\)?

In the middle of an empty pool there is a square platform of \(50 \times 50\) cm, split into cells of \(10\times 10\) cm. Sunny builds towers of \(10\times 10\times 10\)cm cubes on the platform cells. After that his friend Margo turns on the water and counts how many towers are still above the water level. They call each visible tower an island.

For example, let’s consider the case when the heights of the towers are as given in the table on the right. Then at the water level of \(5\) cm there is \(1\) island, at the water level of \(15\) cm there are two islands (if the islands have a common corner or don’t intersect at all, they are considered separate islands), and at the water level of \(25\) cm, all the towers are covered with water and there are \(0\) islands.

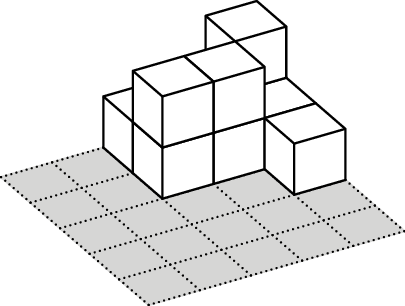
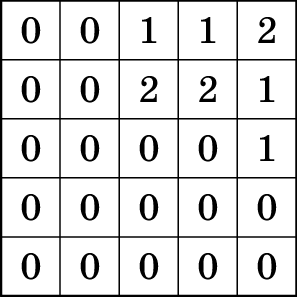
Find out how Sunny should build his towers to get the following numbers of islands corresponding to the level of water in the pool: \[\begin{array}{@{}*{26}{c}@{}} \textit{Water level (cm)}& 5& 15& 25& 35& 45\\ \textit{Number of islands}& 2& 5& 2& 5& 0 \end{array}\]

In the solution, write down how many cubes are there composing a tower in each cell as it is done in the example.

The king possesses \(7\) bags of gold coins, each containing \(100\) coins. While the coins in each bag appear identical, they vary in weight and they cannot be told apart by looking. The king recalls that within these bags, one contains coins that weigh \(7\)g each, another has coins weighing \(8\)g, the third bag contains coins weighing \(9\)g, the fourth has coins weighing \(10\)g, the fifth contains coins weighing \(11\)g, the sixth holds coins weighing \(12\)g, and finally, the seventh bag contains coins weighing \(13\)g each. However, he cannot remember which bag corresponds to which coin weight.
The king reported his situation to his chancellor, pointing to one of the bags, and asked how to determine the weight of the coins in that bag. The chancellor has large two-cup scales without weights. These scales can precisely indicate whether the weights on the cups are equal or, if not, which cup is heavier. Can the chancellor ascertain which coins are in the bag indicated by the king, using no more than two weightings? The chancellor is permitted to take as many coins as necessary to conduct the weightings.

Abigail’s little brother Carson found a big rectangular cake in the fridge and cut a small rectangular piece out of it.

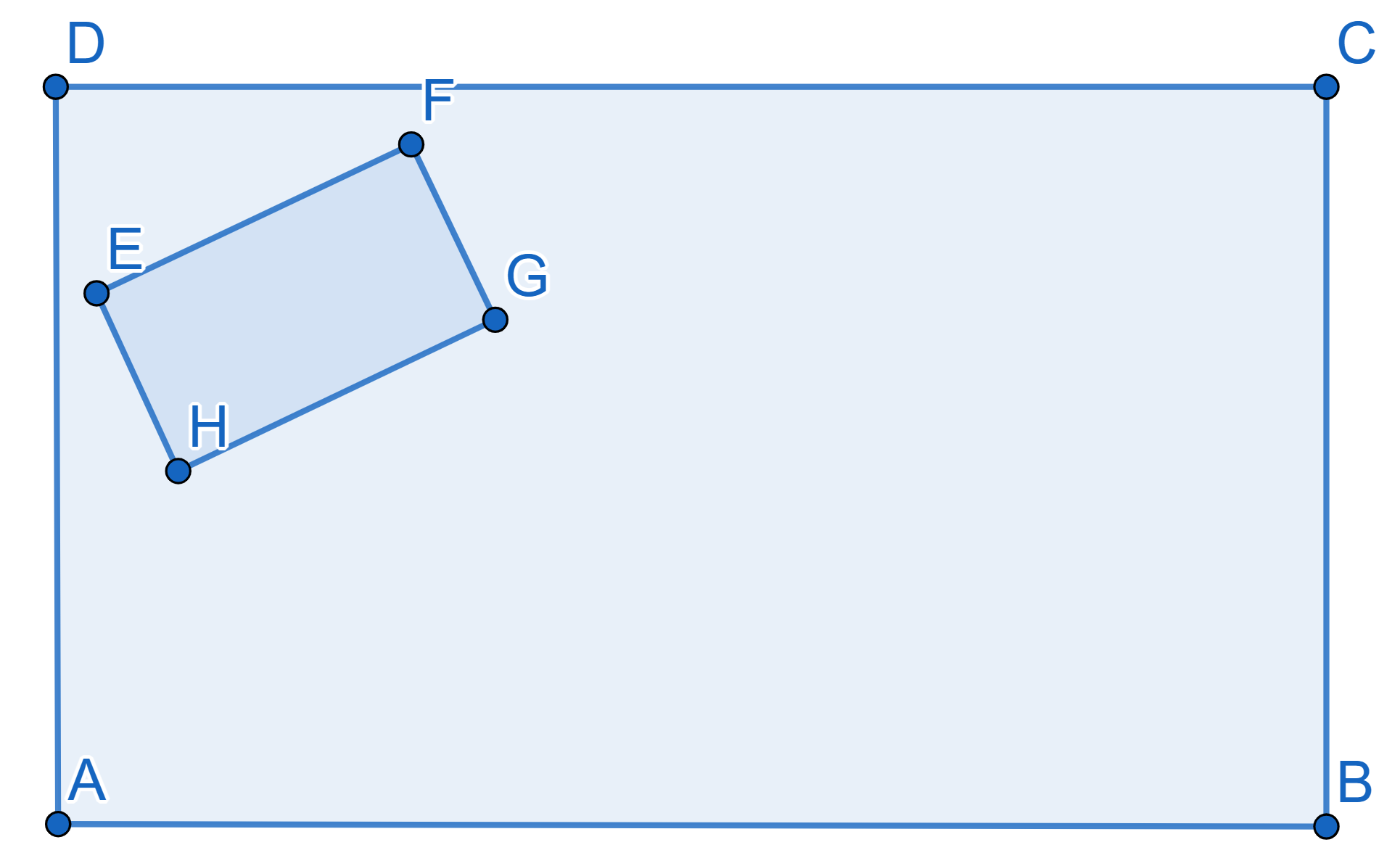
Now Abigail needs to find a way to cut the remaining cake into two pieces of equal area with only one straight cut. How could she do that? The removed piece can be of any size or orientation.

A chord of a circle is a straight line between two points on the circumference of the circle. Is it possible to draw five chords on a circle in such a way that there is a pentagon and two quadrilaterals among the parts into which these chords divide the circle?