Problems

Consider the following "proof" that any triangle is equilateral: Given a triangle \(ABC\), we first prove that \(AB = AC\). First let’s draw the bisector of the angle \(\angle A\). Now draw the perpendicular bisector of segment \(BC\), denote by \(D\) the middle of \(BC\) and by \(O\) the intersection of these lines. See the diagram

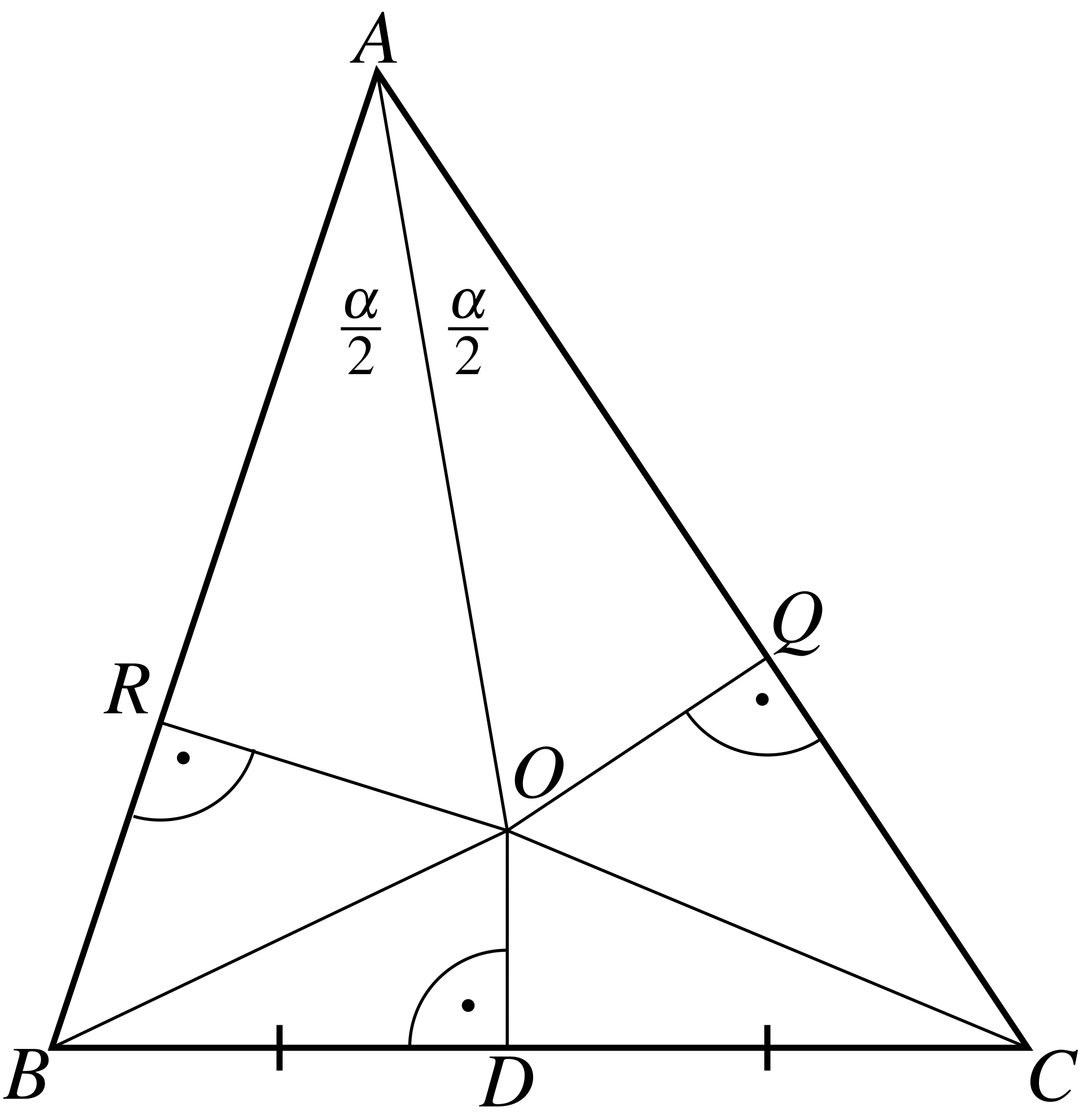
Draw the lines \(OR\) perpendicular to \(AB\) and \(OQ\) perpendicular to \(AC\). Draw lines \(OB\) and \(OC\). Then the triangles, \(RAO\) and \(QAO\) are equal, since we have equal angles \(\angle ORA = \angle OQA = 90°,\) and \(\angle RAO = \angle QAO,\) and the common side \(AO\). On the other hand the triangles \(ROB\) and \(QOC\) are also equal since the angles \(\angle BRO = \angle CQO = 90°\), the hypotenuses \(BO = OC\) the legs \(RO = OQ\). Thus, \(AR = AQ,\) \(RB = QC,\) and \(AB = AR + RB = AQ + QC = AC.\) Q.E.D.

As a corollary, one can show that all the triangles are equilateral, by showing that \(AB = BC\) in the same way.

Let’s prove the following statement: every graph without isolated vertices is connected.
Proof We use the induction on the number of vertices. Clearly the statement is true for graphs with \(2\) vertices. Now, assume we have proven the statement for graphs with up to \(n\) vertices.
Take a graph with \(n\) vertices by induction hypothesis it must be connected. Let’s add a non-isolated vertex to it. As this vertex is not isolated, it is connected to one of the other \(n\) vertices. But then the whole graph of \(n+1\) vertices is connected!

Nick writes the numbers \(1,2,\dots,33\), each exactly once, at the vertices of a polygon with \(33\) sides, in some order.

For each side of the polygon, his little sister Hannah writes down the sum of the two numbers at its ends. In total she writes down \(33\) numbers, one for each side.

It turns out that when read in order around the polygon, these \(33\) sums are \(33\) consecutive whole numbers.

Can you find an arrangement of the numbers written by Nick that makes this happen?

Is it possible to arrange the numbers \(1,\, 2,\, ...,\, 50\) at the vertices and middles of the sides of a regular \(25\)-gon so that the sum of the three numbers at the ends and in the middle of each side is the same for all sides?

Draw a shape that can both be cut into 4 copies of the figure on the left or alternatively into 5 copies of the figure on the right. (the figures can be rotated).

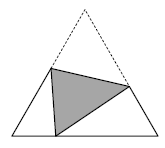
A equilateral triangle made of paper bends in a straight line so that one of the vertices falls on the opposite side as shown on the picture. Show that the corresponding angles of the two white triangles are equal.

Draw how Robinson Crusoe should use pegs, ropes, and sliding rings to tie his goat in order for the goat to graze grass in the shape of a square.

Draw how Robinson Crusoe should put pegs and ropes to tie his goat in order for the goat to graze grass in the shape of a parallelogram.

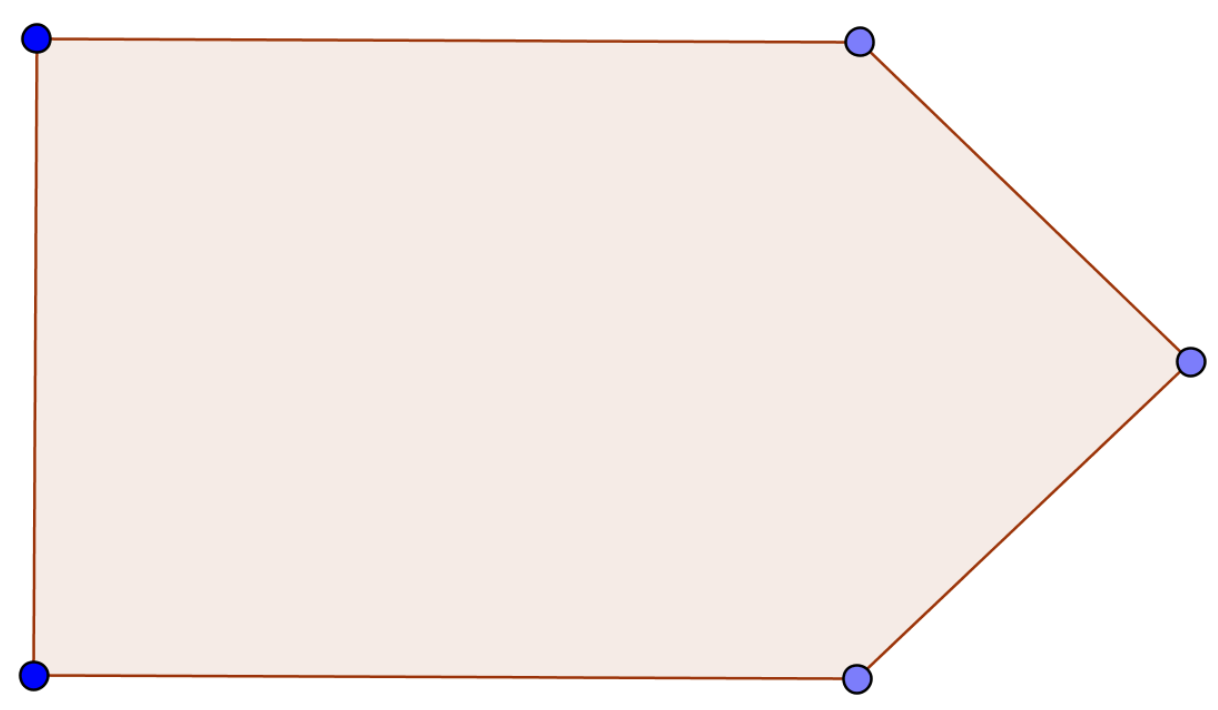
Draw how Robinson Crusoe should put pegs and ropes to tie his goat in order for the goat to graze grass in an area of the following shape:

Draw how Robinson Crusoe should put pegs and ropes to tie his goat in order for the goat to graze grass in the shape of a given triangle.