Problems
Look at the diagram below, which shows how to rearrange the pieces forming the first triangle.
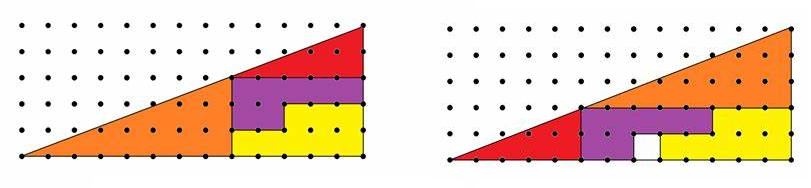
The shape seems unchanged, yet after looking more closely, we see that
the second picture appears to contain one extra square of area. How can
this be?
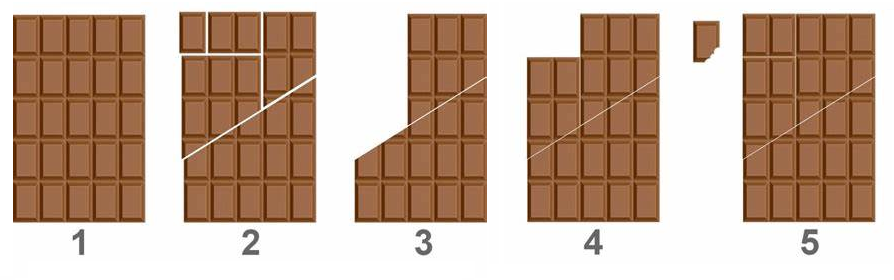
This problem is often called "The infinite chocolate bar". Depicted
below is a way to get one more piece of chocolate from the \(5\times 6\) chocolate bar. Do you see where
is it wrong?
Consider the following "proof" that any triangle is equilateral:
Given a triangle \(ABC\), we first
prove that \(AB = AC\). First let’s
draw the bisector of the angle \(\angle
A\). Now draw the perpendicular bisector of segment \(BC\), denote by \(D\) the middle of \(BC\) and by \(O\) the intersection of these lines. See
the diagram
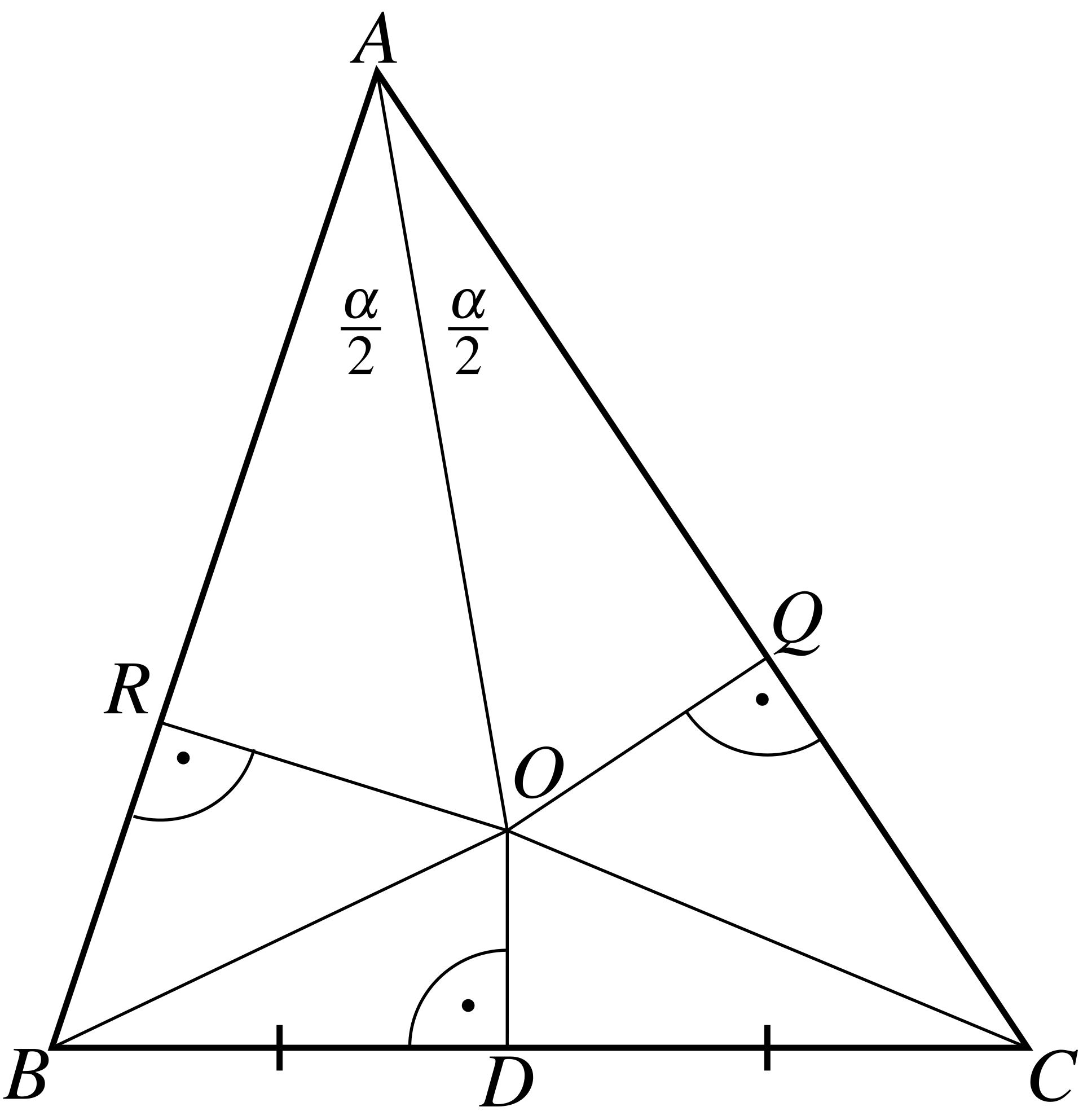
Draw the lines \(OR\) perpendicular to
\(AB\) and \(OQ\) perpendicular to \(AC\). Draw lines \(OB\) and \(OC\). Then the triangles, \(RAO\) and \(QAO\) are equal, since we have equal angles
\(\angle ORA = \angle OQA = 90°,\) and
\(\angle RAO = \angle QAO,\) and the
common side \(AO\). On the other hand
the triangles \(ROB\) and \(QOC\) are also equal since the angles \(\angle BRO = \angle CQO = 90°\), the
hypotenuses \(BO = OC\) the legs \(RO = OQ\). Thus, \(AR = AQ,\) \(RB =
QC,\) and \(AB = AR + RB = AQ + QC =
AC.\) Q.E.D.
As a corollary, one can show that all the triangles are equilateral, by showing that \(AB = BC\) in the same way.
Let’s prove the following statement: every graph without isolated
vertices is connected.
Proof We use the induction on the number of vertices.
Clearly the statement is true for graphs with \(2\) vertices. Now, assume we have proven
the statement for graphs with up to \(n\) vertices.
Take a graph with \(n\) vertices by
induction hypothesis it must be connected. Let’s add a non-isolated
vertex to it. As this vertex is not isolated, it is connected to one of
the other \(n\) vertices. But then the
whole graph of \(n+1\) vertices is
connected!
Nick has written in some order all the numbers \(1,2,...33\) at the vertices of a regular \(33\)-gon. His little sister Hannah assigned to each side of the \(33\)-gon the number equal to the sum of the numbers at the ends of that side. It turns out that Hannah obtained \(33\) consecutive numbers in certain order. Can you find an arrangement of numbers as written by Nick which lead to this situation?
Is it possible to arrange the numbers \(1,\, 2,\, ...,\, 50\) at the vertices and middles of the sides of a regular \(25\)-gon so that the sum of the three numbers at the ends and in the middle of each side is the same for all sides?
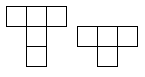
Draw a shape that can be cut into \(4\) copies of the figure on the left or
into \(5\) copies of the figure on the
right (the figures can be rotated).
A equilateral triangle made of paper bends in a straight line so that
one of the vertices falls on the opposite side as shown on the picture.
Show that the corresponding angles of the two white triangles are
equal.
Sometimes proof of a statement requires elaborate reasoning, but sometimes it enough to provide an example when the described construction works. Often enough the problem is asking whether an event is possible, or if an object exists under certain conditions making the existence seemingly unlikely, in such cases all you need to do is to provide an example to solve the problem. Today we will see how to construct such examples.
In a lot of geometric problems the main idea is to find congruent figures. We call two polygons congruent if all their corresponding sides and angles are equal. Triangles are the easiest sort of polygons to deal with. Assume we are given two triangles \(ABC\) and \(A_1B_1C_1\) and we need to check whether they are congruent or not, some rules that help are:
If all three corresponding sides of the triangles are equal, then the triangles are congruent.
If, in the given triangles \(ABC\) and \(A_1B_1C_1\), two corresponding sides \(AB=A_1B_1\), \(AC=A_1C_1\) and the angles between them \(\angle BAC = \angle B_1A_1C_1\) are equal, then the triangles are congruent.
If the sides \(AB=A_1B_1\) and pairs of the corresponding angles next to them \(\angle CAB = \angle C_1A_1B_1\) and \(\angle CBA = \angle C_1B_1A_1\) are equal, then the triangles are congruent.
At a previous geometry lesson we have derived these rules from the axioms of Euclidean geometry, so now we can just use them.