Problems
Author: A.A. Egorov
Calculate the square root of the number \(0.111 \dots 111\) (100 ones) to within a) 100; b) 101; c)* 200 decimal places.
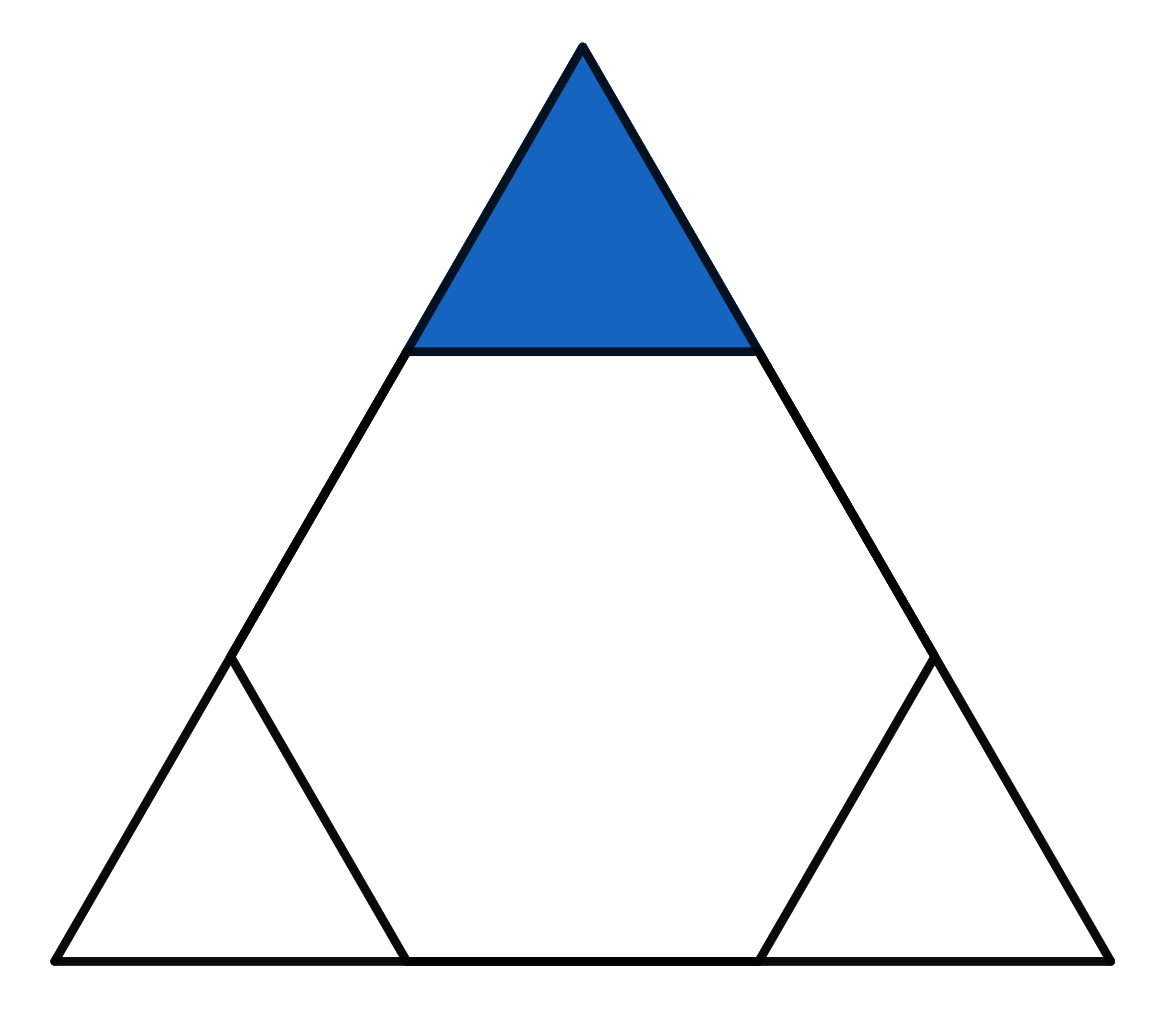
The triangle visible in the picture is equilateral. The hexagon inside is a regular hexagon. If the area of the whole big triangle is \(18\), find the area of the small blue triangle.
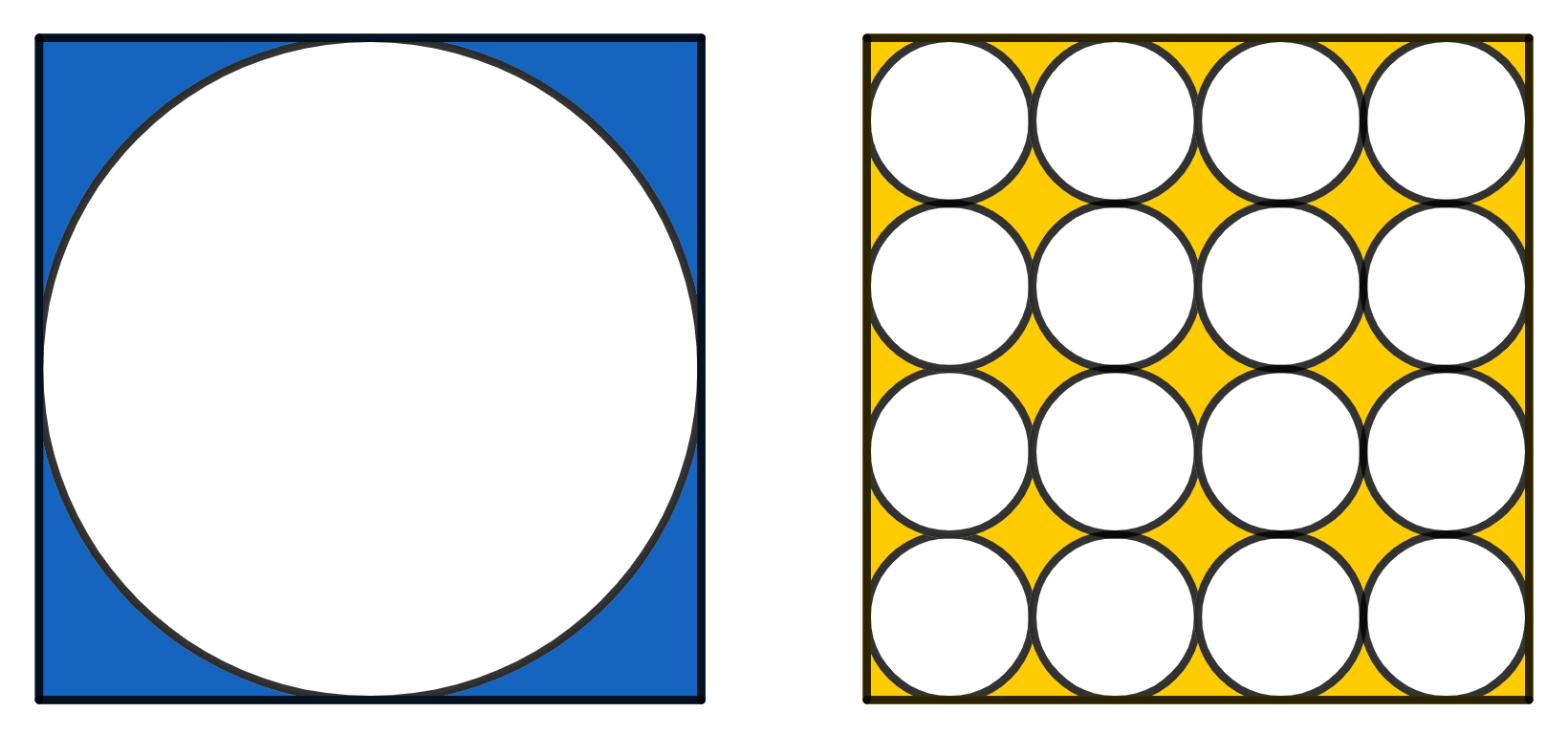
On the left there is a circle inscribed in a square of side 1. On the right there are 16 smaller, identical circles, which all together fit inside a square of side 1. Which area is greater, the yellow or the blue one?
Two people play a game with the following rules: one of them guesses a set of integers \((x_1, x_2, \dots , x_n)\) which are single-valued digits and can be either positive or negative. The second person is allowed to ask what is the sum \(a_1x_1 + \dots + a_nx_n\), where \((a_1, \dots ,a_n)\) is any set. What is the smallest number of questions for which the guesser recognizes the intended set?
Airlines connect pairs of cities. How can you connect 50 cities with the fewest number of airlines so that from every city you can get to any other city by taking at most two flights?
Two lines on the plane intersect at an angle \(\alpha\). On one of them there is a flea. Every second it jumps from one line to the other (the point of intersection is considered to belong to both straight lines). It is known that the length of each of her jumps is 1 and that she never returns to the place where she was a second ago. After some time, the flea returned to its original point. Prove that for the angle \(\alpha\) the value \(\alpha/\pi\) is a rational number.
The White Rook pursues a black horse on a board of \(3 \times 1969\) cells (they walk in turn according to the usual rules). How should the rook play in order to take the horse? White makes the first move.
In a set there are 100 weights, each two of which differ in mass by no more than 20 g. Prove that these weights can be put on two cups of weighing scales, 50 pieces on each one, so that one cup of weights is lighter than the other by no more than 20 g.
Peter bought an automatic machine at the store, which for 5 pence multiplies any number entered into it by 3, and for 2 pence adds 4 to any number. Peter wants, starting with a unit that can be entered free of charge to get the number 1981 on the machine number whilst spending the smallest amount of money. How much will the calculations cost him? What happens if he wants to get the number 1982?
Izzy wrote a correct equality on the board: \(35 + 10 - 41 = 42 + 12 - 50\), and then subtracted 4 from both parts: \(35 + 10 - 45 = 42 + 12 - 54\). She noticed that on the left hand side of the equation all of the numbers are divisible by 5, and on the right hand side by 6. Then she took 5 outside of the brackets on the left hand side and 6 on the right hand side and got \(5(7 + 2 - 9)4 = 6(7 + 2 - 9)\). Having simplified both sides by a common multiplier, Izzy found that \(5 = 6\). Where did she go wrong?