There was a football match of 10 versus 10 players between a team of liars (who always lie) and a team of truth-tellers (who always tell the truth). After the match, each player was asked: “How many goals did you score?” Some participants answered “one”, Callum said “two”, some answered “three”, and the rest said “five”. Is Callum lying if it is known that the truth-tellers won with a score of 20:17?
Out of the given numbers 1, 2, 3, ..., 1000, find the largest number \(m\) that has this property: no matter which \(m\) of these numbers you delete, among the remaining \(1000 - m\) numbers there are two, of which one is divisible by the other.
Author: A.A. Egorov
Calculate the square root of the number \(0.111 \dots 111\) (100 ones) to within a) 100; b) 101; c)* 200 decimal places.
A rectangular chocolate bar size \(5 \times 10\) is divided by vertical and horizontal division lines into 50 square pieces. Two players are playing the following game. The one who starts breaks the chocolate bar along some division line into two rectangular pieces and puts the resulting pieces on the table. Then players take turns doing the same operation: each time the player whose turn it is at the moment breaks one of the parts into two parts. The one who is the first to break off a square slice \(1\times 1\) (without division lines) a) loses; b) wins. Which of the players can secure a win: the one who starts or the other one?
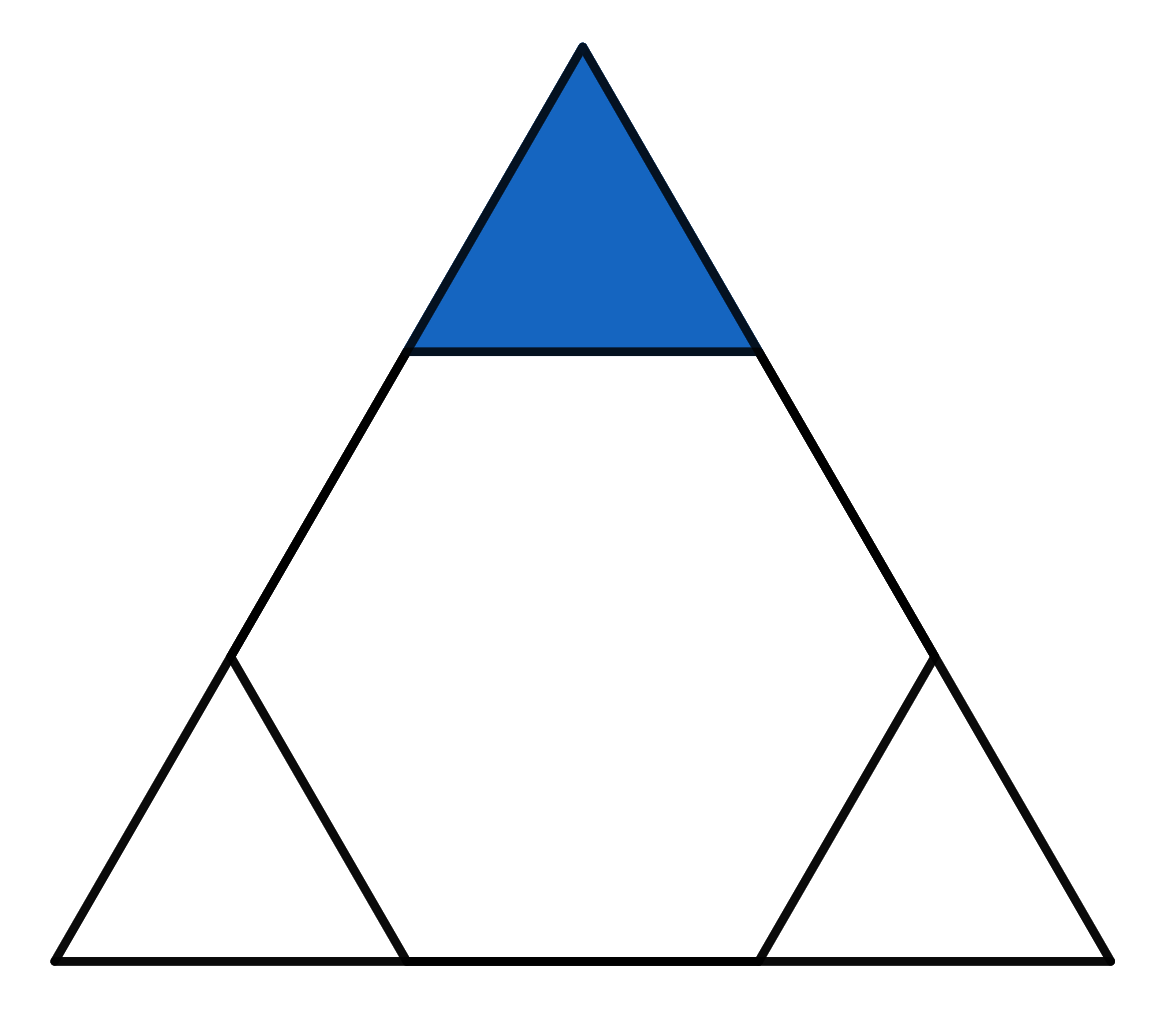
The triangle visible in the picture is equilateral. The hexagon inside is a regular hexagon. If the area of the whole big triangle is \(18\), find the area of the small blue triangle.
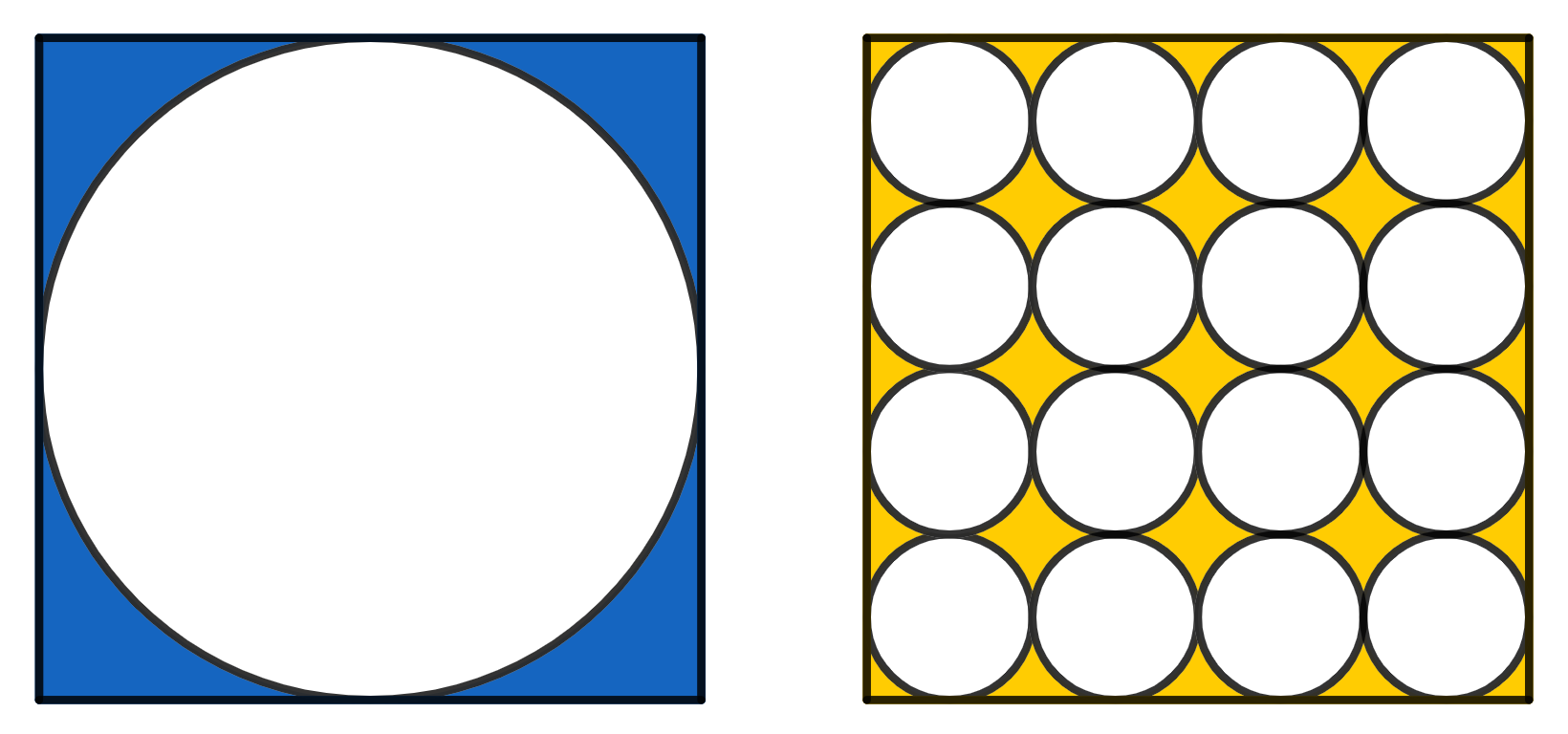
On the left there is a circle inscribed in a square of side 1. On the right there are 16 smaller, identical circles, which all together fit inside a square of side 1. Which area is greater, the yellow or the blue one?
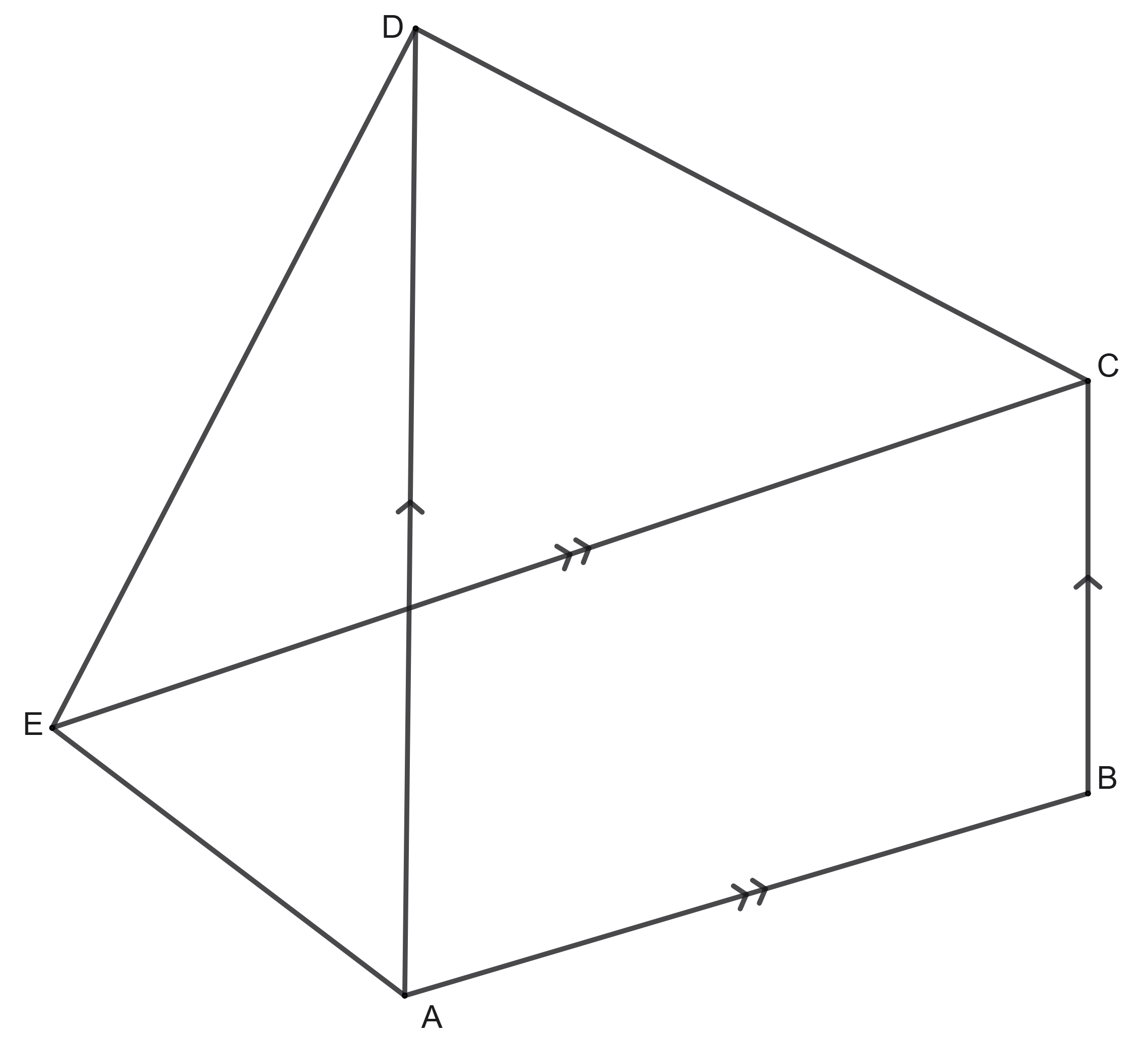
In a pentagon \(ABCDE\), diagonal \(AD\) is parallel to the side \(BC\) and the diagonal \(CE\) is parallel to the side \(AB\). Show that the areas of the triangles \(\triangle ABE\) and \(\triangle BCD\) are the same.
Prove that, for any integer \(n\), among the numbers \(n, n + 1, n + 2, \dots , n + 9\) there is at least one number that is mutually prime with the other nine numbers.
How can you arrange the numbers \(5/177\), \(51/19\) and \(95/9\) and the arithmetical operators “\(+\)”, “\(-\)”, “\(\times\)” and “\(\div\)” such that the result is equal to 2006? Note: you can use the given numbers and operators more than once.
There are 13 weights, each weighing an integer number of grams. It is known that any 12 of them can be divided into two cups of weights, six weights on each one, which will come to equilibrium. Prove that all the weights have the same weight.