Problems
On a certain island there are \(17\) grey, \(15\) brown and \(13\) crimson chameleons. If two chameleons of different colours meet, then both of them change into the third colour. No other colour changes are allowed. Is it possible that, after a number of such colour changes, all the chameleons have the same colour?
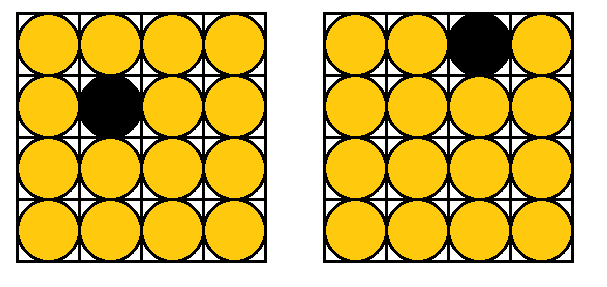
Sixteen lightbulbs are arranged in a \(4 \times 4\) grid. Some of them are on, the other ones are off. You are allowed to change the state of all the bulbs in a column, in a row, or along any diagonal (note: there are \(14\) diagonals in total!). Is it possible to go from the arrangement on the left to the one on the right by repeating this operation?
The numbers \(1\) to \(2025\) are written on a board. In one move, we may erase any two numbers and replace them with the absolute value of their difference. Can we, after some number of moves, end up with a sequence consisting only of \(0\)?
Hard. Let \(\mathcal{S}\) be a finite set of at least two points in the plane. Assume that no three points of \(\mathcal S\) are collinear. A windmill is a process that starts with a line \(\ell\) going through a single point \(P \in \mathcal S\). The line rotates clockwise about the pivot \(P\) until the first time that the line meets some other point belonging to \(\mathcal S\). This point, \(Q\), takes over as the new pivot, and the line now rotates clockwise about \(Q\), until it next meets a point of \(\mathcal S\). This process continues indefinitely. Show that we can choose a point \(P\) in \(\mathcal S\) and a line \(\ell\) going through \(P\) such that the resulting windmill uses each point of \(\mathcal S\) as a pivot infinitely many times.
In the quadrilateral \(ABCD\) the
diagonals \(AC\) and \(BD\) intersect at the point \(E\). It is known that the perimeter of the
triangle \(ABC\) is equal to the
perimeter of the triangle \(ABD\), and
the perimeter of the triangle \(ACD\)
equals the perimeter of the triangle \(BCD\).
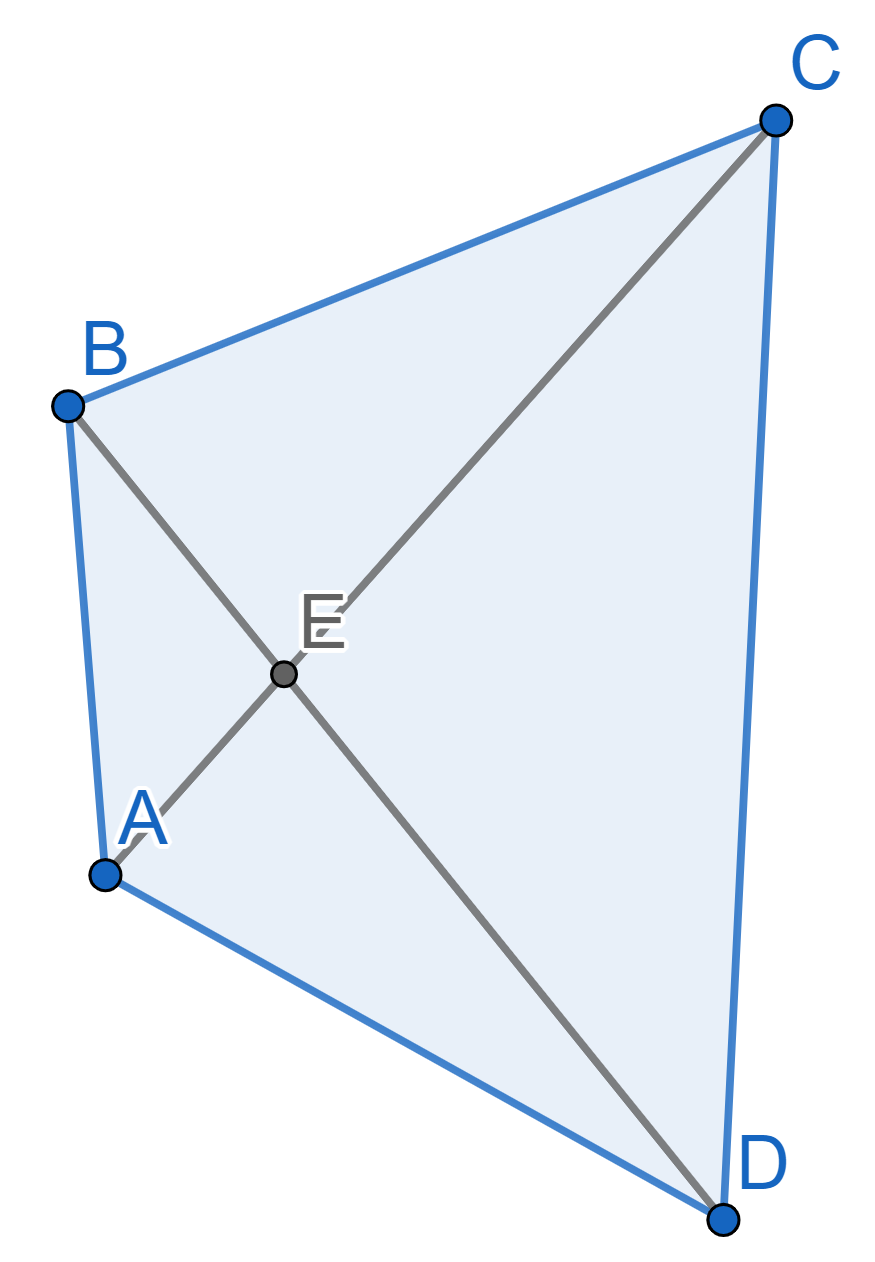
Prove that \(AE=BE\).
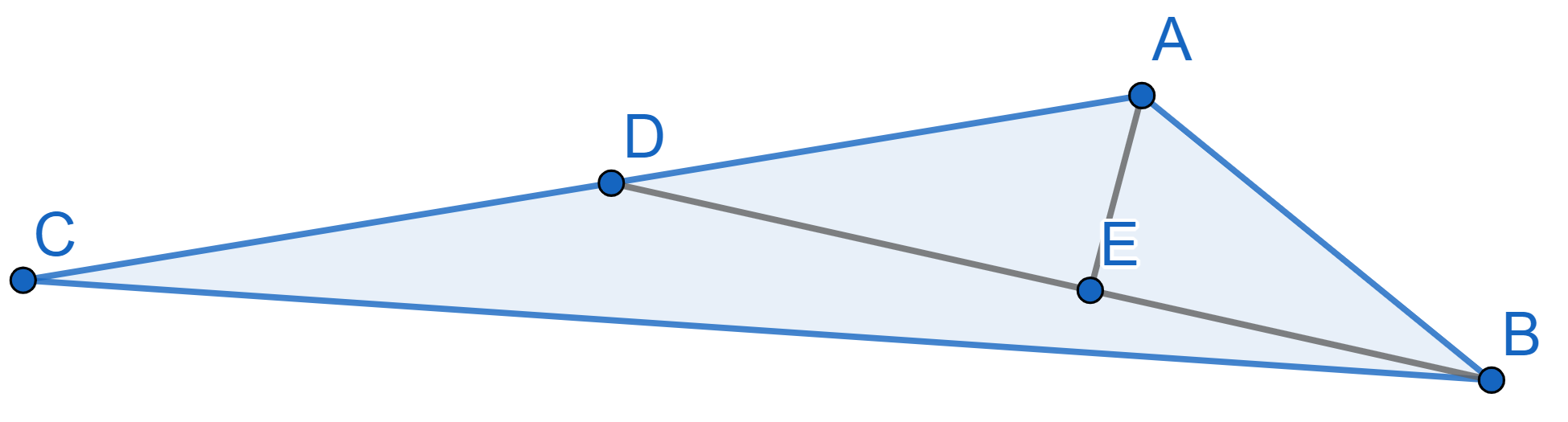
In the triangle \(ABC\) the segment
\(AB=5\) and the segment \(BD\) is the median. The segment \(AE\) is perpendicular to \(BD\) and divides \(BD\) in half. Find the length of \(AC\).
A magic square is a square filled with numbers, one in each cell, in such a way that the sums of the numbers in each row, each column and along each of the two main diagonals are the same. The value of this sum is known as the magic constant of the square. Show that in any \(4 \times 4\) magic square (which contains \(16\) numbers) the sum of all the numbers in the \(4\) central squares is also equal to the magic constant of the square.
Show that for any natural number \(n\geq 1\), the number \[n^4+4n^2+9\] is not a perfect square.
There are \(12\) light bulbs placed on top of the numbers on a clock face. Initially, only the bulb at \(12\) is on. We can choose any \(6\) consecutive bulbs and change their state simultaneously, that is, if any were on, we turn them off, if any were off, we turn them on. Can we perform this operation multiple times so that in the end only the bulb at \(11\) is on?
A group of schoolboys are going to walk down a narrow path in a straight line, one behind the other. There are \(11\) boys, and among them are Will, Tom, and Alex. If exactly two of them walk directly next to each other, they will start arguing. But if the three of them are all next to each other, in any order, the third one will always break the argument of the other two. We don’t want any arguments to persist. How many ways are there to order all \(11\) boys?