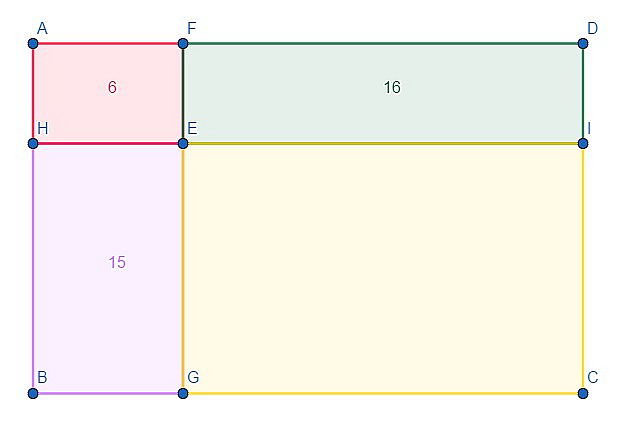
Problems
Today’s topic is inequalities, expressions like \(a\geq b\), or \(a>b\). There are certain rules for operating inequalities: one can subtract the same number from both sides of the inequality, namely if \(a\geq b\), then \(a-b \geq 0\). If \(a \geq b\) and \(b\geq c\), then \(a\geq c\). If a number \(c\geq 0\), then from \(a\geq b\) it follows that \(ac \geq bc\). However, in case of multiplication by a negative number \(c\leq 0\), the inequality sign reverses: from \(a\geq b\) it follows that \(ac \leq bc\). One should also remember that the square of any real number is non-negative.
Draw how Robinson Crusoe should use pegs, ropes, and sliding rings to tie his goat in order for the goat to graze grass in the shape of a square.
Draw how Robinson Crusoe should put pegs and ropes to tie his goat in order for the goat to graze grass in the shape of a parallelogram.
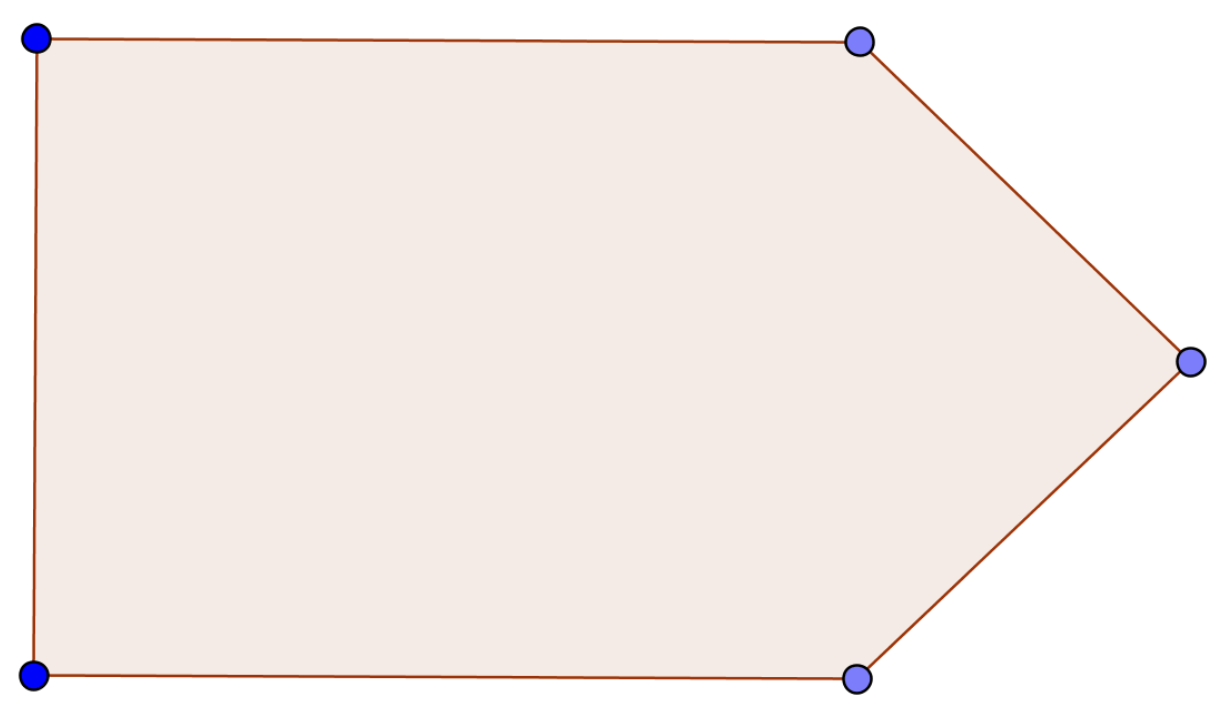
Draw how Robinson Crusoe should put pegs and ropes to tie his goat in order for the goat to graze grass in an area of the following shape:
Draw how Robinson Crusoe should put pegs and ropes to tie his goat in order for the goat to graze grass in the shape of a given triangle.
Draw how Robinson Crusoe should arrange pegs and ropes so that his goat grazes in the shape of a hexagon. The hexagon doesn’t need to be regular.
Robinson Crusoe’s goat is tied to a single peg with one rope. Draw how Robinson should arrange pegs, ropes, a sliding ring, and a wolf so that the goat grazes in the shape of a half-circle.
One day, Robinson found a wolf in the island. He took the wolf with him and tied it with a rope to a peg. Robinson noticed that the goat would not graze anywhere that the wolf could reach. How could Robinson arrange both animals with pegs and ropes so that the goat can only graze in the shape of a waning moon? (see picture below)

Draw how Robinson Crusoe should arrange pegs, ropes, and a wolf so that the goat grazes grass in the shape of a half-ring.