Problems
Anna has a garden of square shape with side \(4\) m. After playing with her dog in the garden she left \(5\) dog toys on the lawn. Show that some two of them are closer than \(3\) m apart.
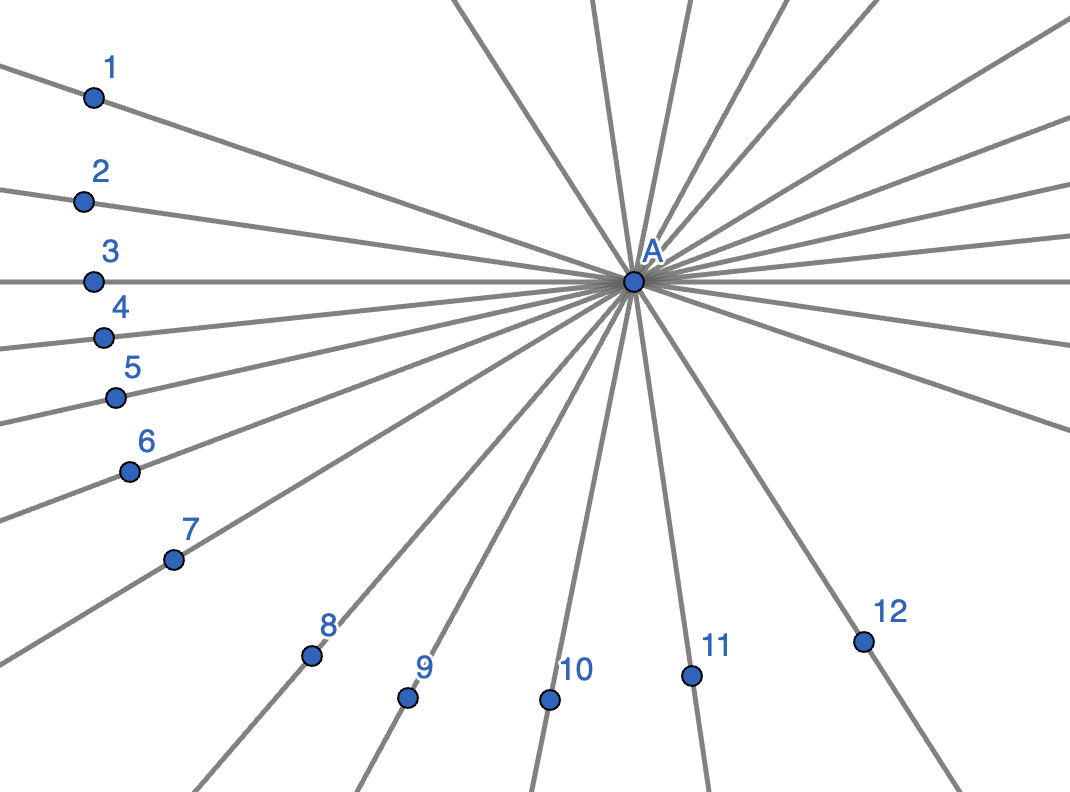
Twelve lines are drawn on the plane, passing through a point \(A\). Prove that there are two of them with angle less than \(17^{\circ}\) between them.
Inside a square of area \(6\), there are three polygons, each of area \(3\). Show that some two of these polygons overlap and the area of the overlap is at least \(1\).
A Wimbledon doubles court is \(78\)ft\(\times36\)ft. After a long practice match, there were \(79\) tennis balls in the court area. Show that some two of the balls were at most \(6\sqrt{2}\)ft away from each other.
There are \(n\) ambassadors, each from a different country, sitting at a round table. The flag for each country is on the table, but unfortunately the flags have been mixed up. As a result each ambassador has a wrong flag in front of them, while their flag is in front of some other ambassador. Show that you can rotate the table with the flags on it, in such a way that at least two ambassadors will have correct flags in front of them.
We have an infinitely large chessboard, consisting of white and black squares. We would like to place a stain of a specific shape on this chessboard. The stain is a bounded and connected shape with an area strictly less than the area of one square of the chessboard. Show that it is always possible to place the stain in such a way that it does not cover a vertex of any square.
There are \(n\) straight lines on a plane, no two among them are parallel to each other. Show that some two of them cross at an angle no more than \(\frac{180^{\circ}}{n}\).
Thirteen boys and girls met to play a football match. Eleven of them shook hands with everybody else in the group. The last two shook hands with everybody else but not each other, because they were siblings and arrived together. How many handshakes took place?
The city of Konigsberg has seven bridges as depicted on the layout below. \[\includegraphics[scale=0.5]{https://problems-static.s3.amazonaws.com/production/problem_images/WSP-000146.png}\] Is it possible for the great mathematician Leonard Euler to have an excursion in Konigsberg visiting all islands and land banks, but crossing each bridge exactly once?
There are \(6\) people at a party. Each two people either know each other or not, and the knowledge goes both ways: if \(A\) knows \(B\), then \(B\) knows \(A\). Show that there either is a trio of people who all know each other or a trio of people who all don’t know each other.