The length of the hypotenuse of a right-angled triangle is 3.
a) The Scattered Scientist calculated the dispersion of the lengths of the sides of this triangle and found that it equals 2. Was he wrong in the calculations?
b) What is the smallest standard deviation of the sides that a rectangular triangle can have? What are the lengths of its sides, adjacent to the right angle?
The mathematics teacher suggested changing the voting scheme at the performance competition. Currently, two groups compete in the final. In the first group, there are \(n\) pupils from class 5A, and in the second, there are \(n\) pupils from class 5B. \(2n\) mothers of all \(2n\) students attended the final of the competition. The best performance is chosen by the mothers voting. It is known that exactly half of the mothers vote honestly for the best performance, and the other half, in any case, vote for the performance in which her child participates (see problem number 65299). The teacher believes that it is necessary to choose a jury of \(2m\) people \((2m \ensuremath{\leq} n)\) from all \(2n\) mums at random. Find the probability that the best performance will win under such voting conditions.
A numerical set \(x_1, \dots , x_n\) is given. Consider the function \(d(t) = \frac{min_{i=1,\dots ,n}|x_i-t| + max_{i=1,\dots ,n}|x_i - t|}{2}\).
a) Is it true that the function \(d (t)\) takes the smallest value at a single point, for any set of numbers \(x_1, \dots , x_n\)?
b) Compare the values of \(d (c)\) and \(d (m)\) where \(c = \frac{min_{i=1,\dots ,n}x_i + max_{i=1,\dots ,n}x_i}{2}\) and \(m\) is the median of the specified set.
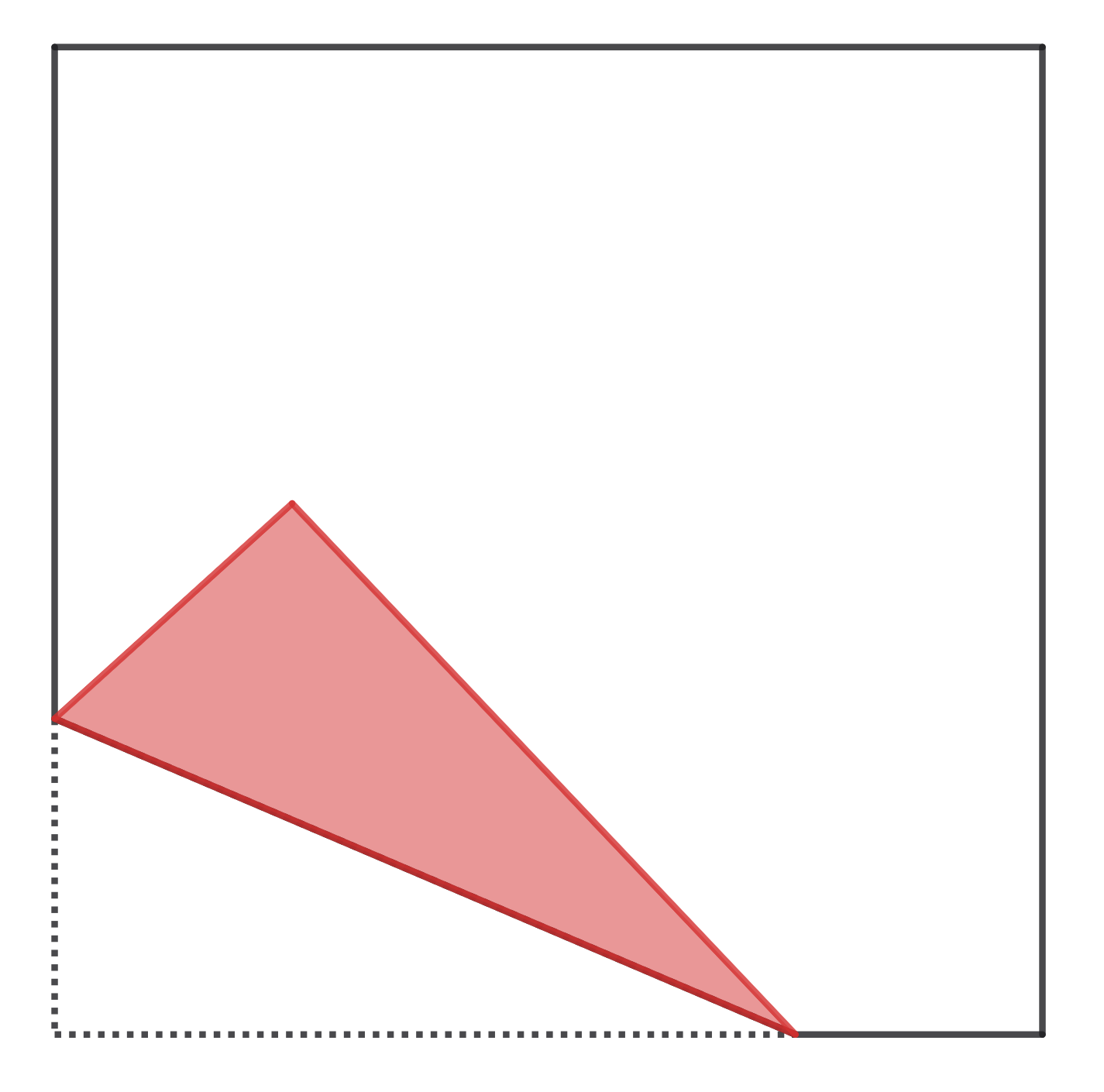
James furiously cuts a rectangular sheet of paper with scissors. Every second he cuts a random piece by an unsystematic rectilinear cut into two parts.
a) Find the mathematical expectation of the number of sides of a polygon (made from a piece of paper) that James randomly picks up after an hour of such work.
b) Solve the same problem if at first the piece of paper had the form of an arbitrary polygon.
The upper side of a piece of square paper is white, and the lower one is red. In the square, a point F is randomly chosen. Then the square is bent so that one randomly selected vertex overlaps the point F. Find the mathematical expectation of the number of sides of the red polygon that appears.
In the Valley of the Five Lakes there are five identical lakes, some of which are connected by streams (in the image, dotted lines denote the possible “routes” of streams). Small carps are born only in lake \(S\). While the carp is growing up, it passes exactly four times from one lake to another by some stream (the carp chooses a stream at random), and then it remains in the lake in which it ended up. Of every thousand carps, an average of 375 remain in lake \(S\), and the rest remain in lake \(B\), no one else lives in the other lakes. Determine how many streams there are in the Valley of the Five Lakes.
A regular dice is thrown many times. Find the mathematical expectation of the number of rolls made before the moment when the sum of all rolled points reaches 2010 (that is, it became no less than 2010).
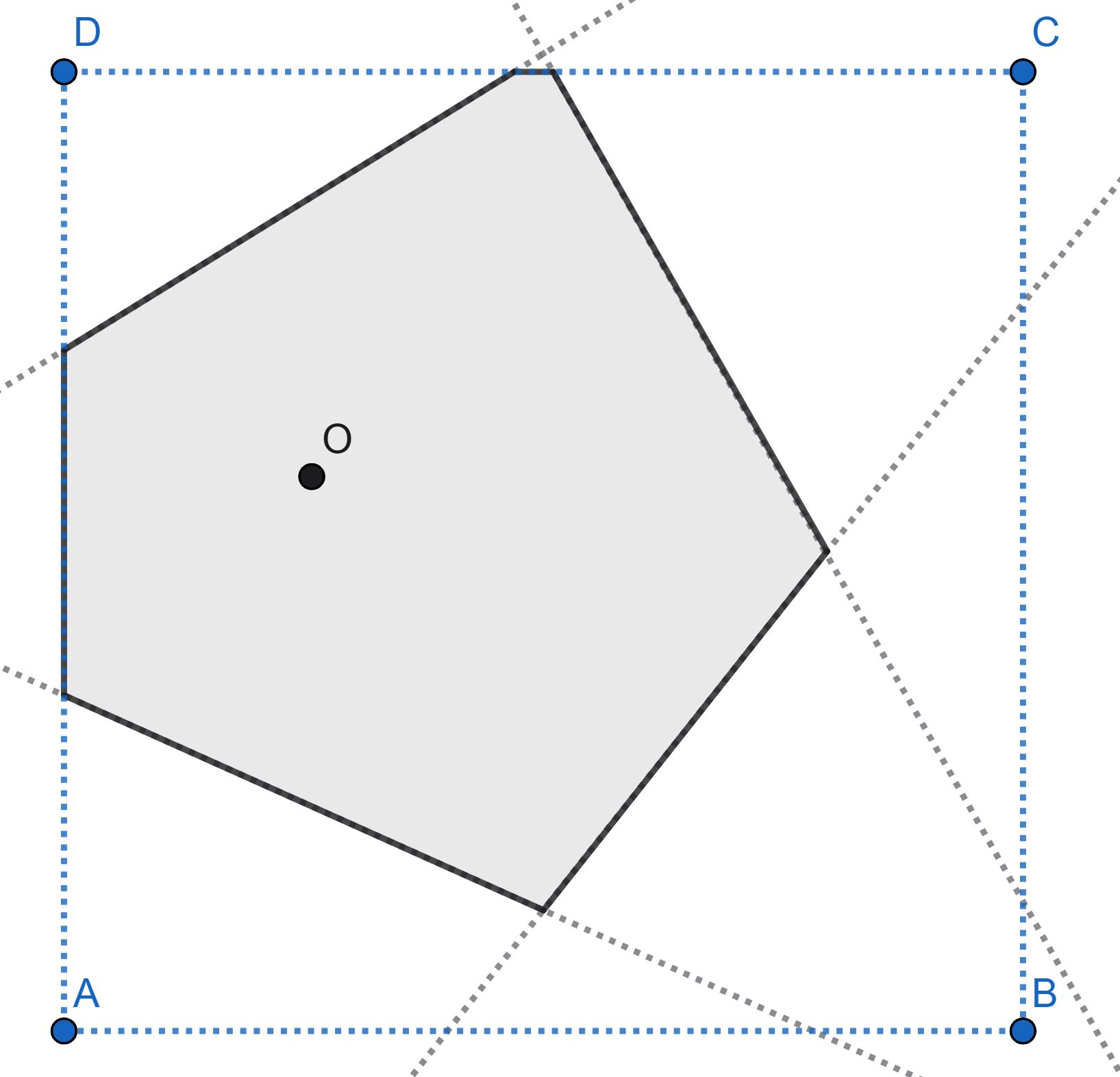
The point \(O\) is randomly chosen on piece of square paper. Then the square is folded in such a way that each vertex is overlaid on the point \(O\). The figure shows one of the possible folding schemes. Find the mathematical expectation of the number of sides of the polygon that appears.
The bus has \(n\) seats, and all of the tickets are sold to \(n\) passengers. The first to enter the bus is the Scattered Scientist and, without looking at his ticket, takes a random available seat. Following this, the passengers enter one by one. If the new passenger sees that his place is free, he takes his place. If the place is occupied, then the person who gets on the bus takes the first available seat. Find the probability that the passenger who got on the bus last will take his seat according to his ticket?
A fair dice is thrown many times. It is known that at some point the total amount of points became equal to exactly 2010.
Find the mathematical expectation of the number of throws made to this point.