Problems
The Scattered Scientist constructed a device consisting of a sensor and a transmitter. The average life expectancy of the sensor part is 3 years, the average lifetime of the transmitter is 5 years. Knowing the distribution of the lifetime of the sensor and the transmitter, the Scattered Scientist calculated that the average lifetime of the entire device is 3 years 8 months. Was the Scattered Scientist wrong in his calculations?
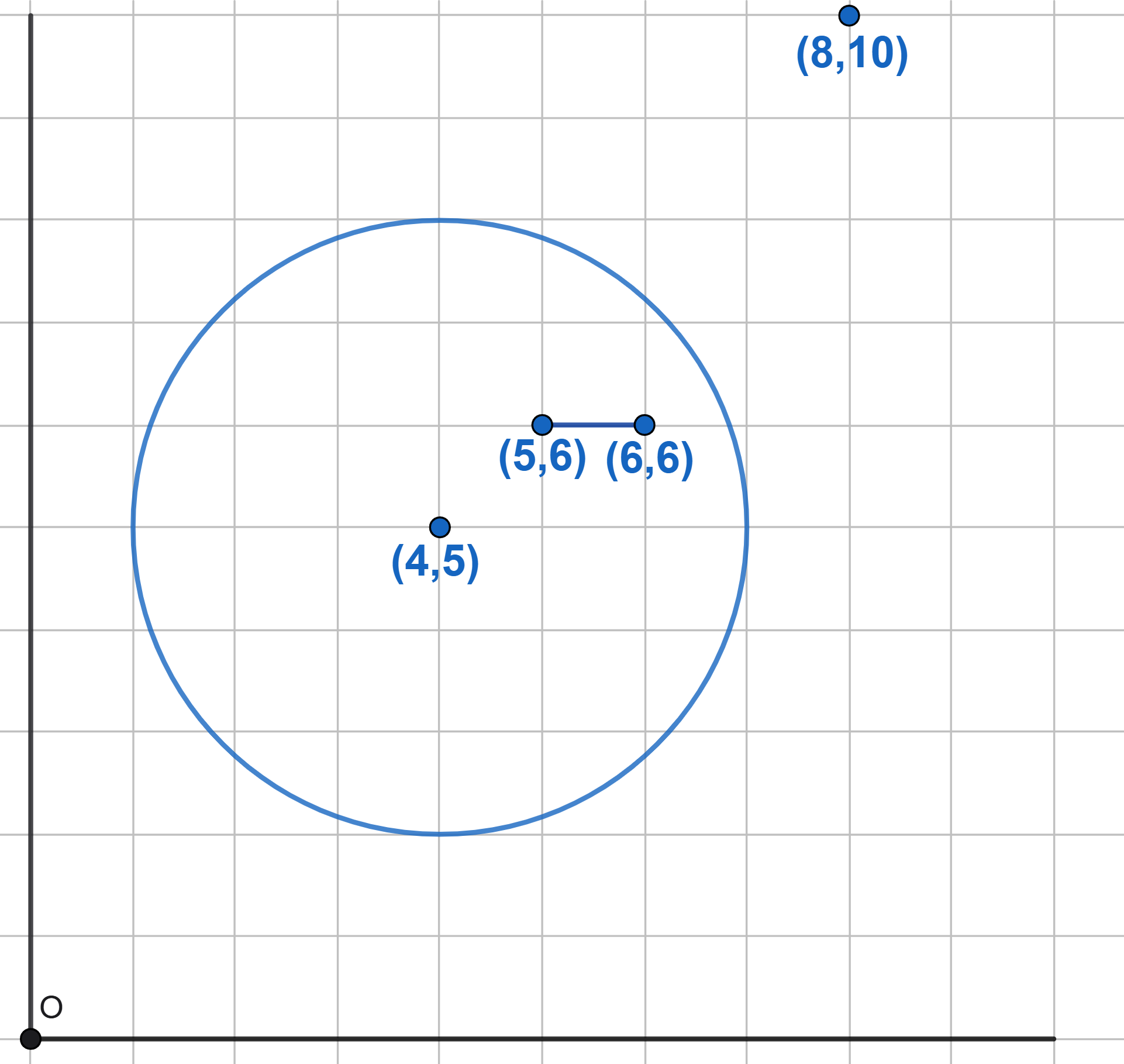
A fly crawls along a grid from the origin. The fly moves only along the lines of the integer grid to the right or upwards (monotonic wandering). In each node of the net, the fly randomly selects the direction of further movement: upwards or to the right. Find the probability that at some point:
a) the fly will be at the point \((8, 10)\);
b) the fly will be at the point \((8, 10)\), along the line passing along the segment connecting the points \((5, 6)\) and \((6, 6)\);
c) the fly will be at the point \((8, 10)\), passing inside a circle of radius 3 with center at point \((4, 5)\).
In a numerical set of \(n\) numbers, one of the numbers is 0 and another is 1.
a) What is the smallest possible variance of such a set of numbers?
b) What should be the set of numbers for this?
The television game “What? Where? When?” consists of a team of “experts” trying to solve 13 questions that are thought up and sent in by the viewers of the programme. Envelopes with the questions are selected in turn in random order with the help of a spinning top with an arrow. If the experts answer correctly, they earn a point, and if they answer incorrectly, the viewers get one point. The game ends as soon as one of the teams scores 6 points. The probability of the team of experts winning in one round is 0.6 and there can be no draws. Currently, the experts are losing 3 to 4. Find the probability that the experts will still win.
A fly moves from the origin only to the right or upwards along the lines of the integer grid (a monotonic wander). In each node of the net, the fly randomly selects the direction of further movement: upwards or to the right.
a) Prove that sooner or later the fly will reach the point with abscissa 2011.
b) Find the mathematical expectation of the ordinate of the fly at the moment when the fly reached the abscissa 2011.
The point \(O\), lying inside the triangle \(ABC\), is connected by segments with the vertices of the triangle. Prove that the variance of the set of angles \(AOB\), \(AOC\) and \(BOC\) is less than a) \(10\pi ^2/27\); b) \(2\pi ^2/9\).
King Arthur has two equally wise advisers – Merlin and Percival. Each of them finds the correct answer to any question with probability \(p\) or an incorrect answer, with probability \(q = 1 - p\).
If both counsellors say the same thing, the king listens to them. If they say opposite things, then the king chooses a solution by tossing a coin.
One day, Arthur thought about why he had two advisers, would one not be enough? Then the king called for his counsellors and said:
“It seems to me that the probability of making the right solutions will not decrease if I keep one adviser and listen to him. If so, I must fire one of you. If not, I’ll leave it as it is. Tell me, should I fire one of you?”.
“Who exactly are you going to fire, King Arthur?”, asked the advisers.
“If I make the solution to fire one of you, I will make a choice by tossing a coin”.
The advisers went to think about the answer. The advisors, we repeat, are equally wise, but not equally honest. Percival is very honest and will try to give the right answer, even if he faces dismissal. And Merlin, honest about everything else, in this situation decides to give such an answer with which the probability of his dismissal is as low as possible. What is the probability that Merlin will be fired?
On the skin of a Rhinoceros, its folds are vertical and horizontal. If the Rhinoceros has \(a\) vertical and \(b\) horizontal folds on the left side, and on the right side – \(c\) vertical and \(d\) horizontal folds, we will say that this is a rhinoceros in the state \((abcd)\) or just an \((abcd)\) rhinoceros.
If the Rhinoceros’ itches one of his sides against a tree in an up-down movement, and Rhinoceros has two horizontal folds on this side, then these two horizontal folds are smoothed out. If there are no two folds like this, then nothing happens.
Similarly, if the Rhinoceros itches on of his sides in a back and forth movement, and on this side, there are two vertical folds, then they are smoothed out. If there are no two folds like this, then nothing happens.
If, on some side, two folds are smoothed out, then on the other side, two new folds immediately appear: one vertical and one horizontal.
The rhinoceroses often have random sides that are itchy and need to be scratched against a tree in random directions.
At first there was a herd of Rhinoceroses in the savannah \((0221)\). Prove that after some time there were Rhinoceros of state \((2021)\) in the savannah.
At the sound of the whistle of the PE teacher, all 10 boys and 7 girls lined up randomly.
Find the mathematical expectation of the value “the number of girls standing to the left of all of the boys.”
Hercules meets the three-headed snake Hydra of Lerna. Every minute, Hercules chops off one head of the snake. Let \(x\) be the survivability of the snake (\(x > 0\)). The probability \(p_s\) of the fact that in the place of the severed head will grow s new heads \((s = 0, 1, 2)\) is equal to \(\frac{x^s}{1 + x + x^2}\).
During the first 10 minutes of the battle, Hercules recorded how many heads grew in place of each chopped off one. The following vector was obtained: \(K = (1, 2, 2, 1, 0, 2, 1, 0, 1, 2)\). Find the value of the survivability of the snake, under which the probability of the vector \(K\) is greatest.