Problems
Is it possible to link three rings together in such a way that they cannot be separate from each other, but if you remove any ring, then the other two will fall apart?
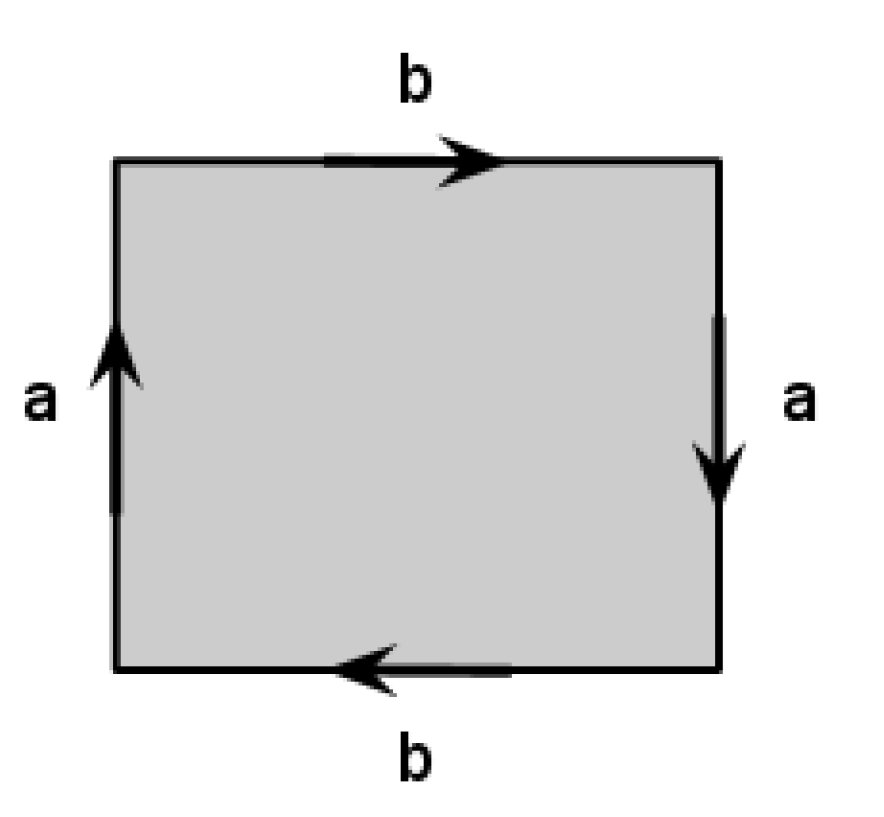
If we glue the opposite sides of the paper band in the same direction as on the picture, we will get a cylinder. What surface do we get, if we glue the circles of the cylinder in the same direction as well?
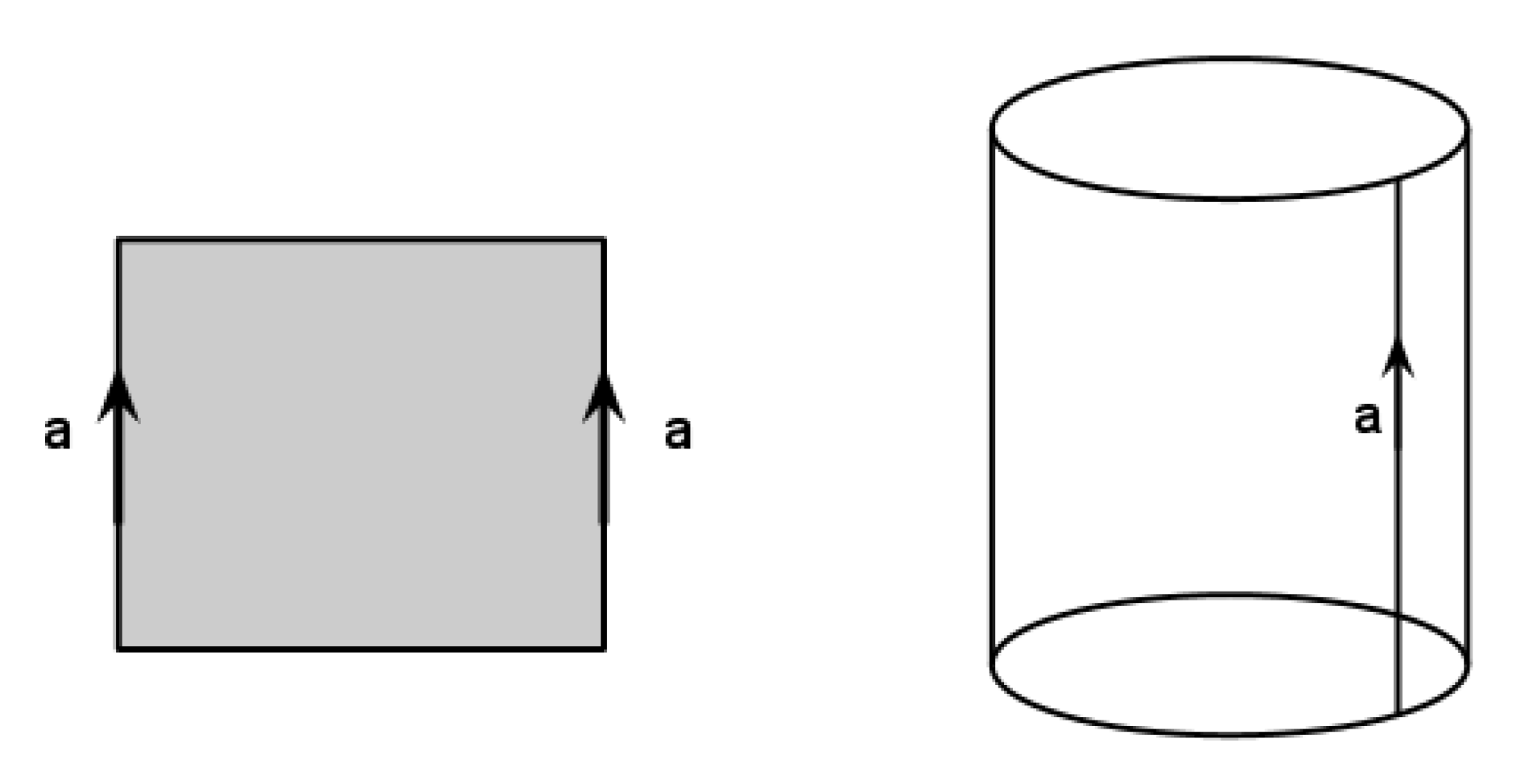
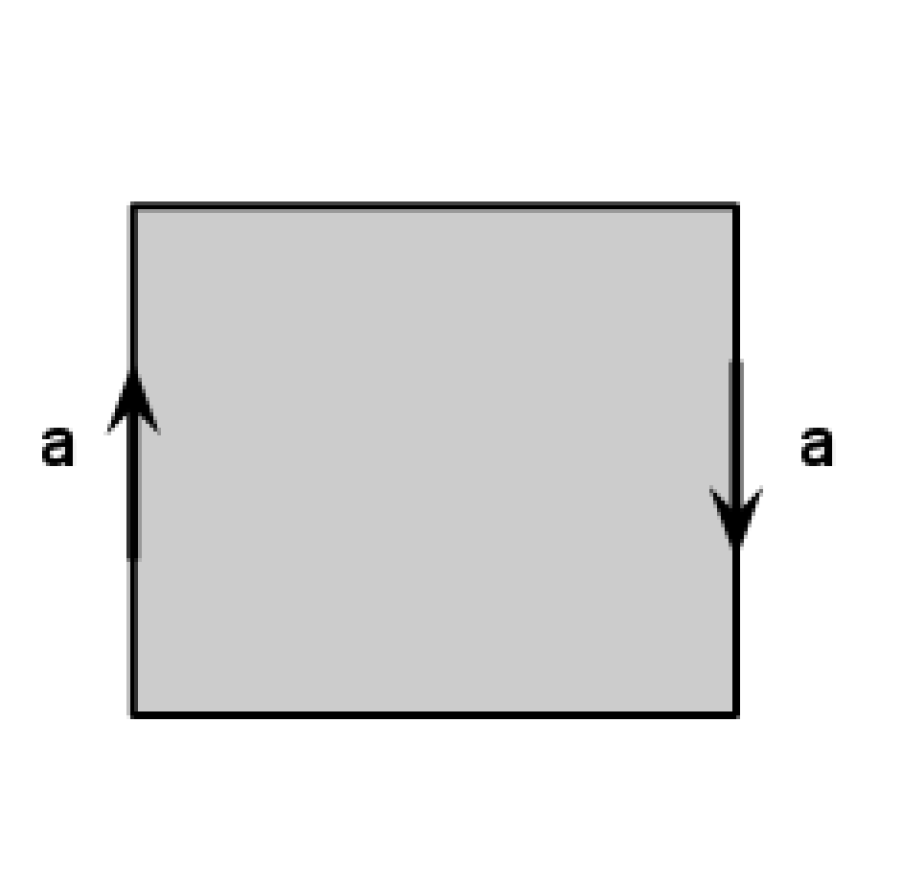
We start with a rectangular sheet of paper - preferably with proportions more than \(6:1\), so that it looks more like a band. For now assume that one can stretch or shrink the paper band as needed. Describe the surface we get if we start with a rectangular sheet of paper and then glue the opposite sides of the paper band in the opposite direction as in the picture.
In the last room, there are two doors, but someone broke into this room and the signs that used to be on the doors are now on the floor! You do not know which sign was on which door, but the statements on them say:
There is a trap behind this door.
There are traps behind both doors.
Your guide says: The first sign is true if there is treasure behind
the first door, otherwise it is false. The second sign is false if there
is treasure behind the second door, otherwise it is true.
But you don’t know which sign is first! What do you do?
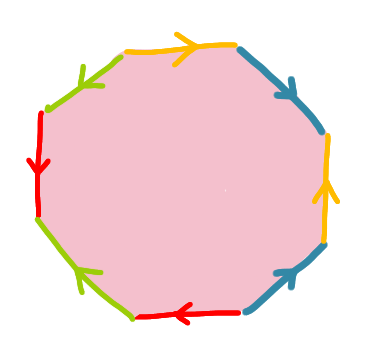
How would you describe the surface obtained by glueing the sides of the octagon as on the picture? Sides of the same colour are glued together in the same direction as shown.
Describe the surface which we can get if we start with a rectangular sheet of paper, make a cylinder by glueing the opposite sides in the same direction and then glue the other opposite sides of the paper band in the opposite direction as on the picture.
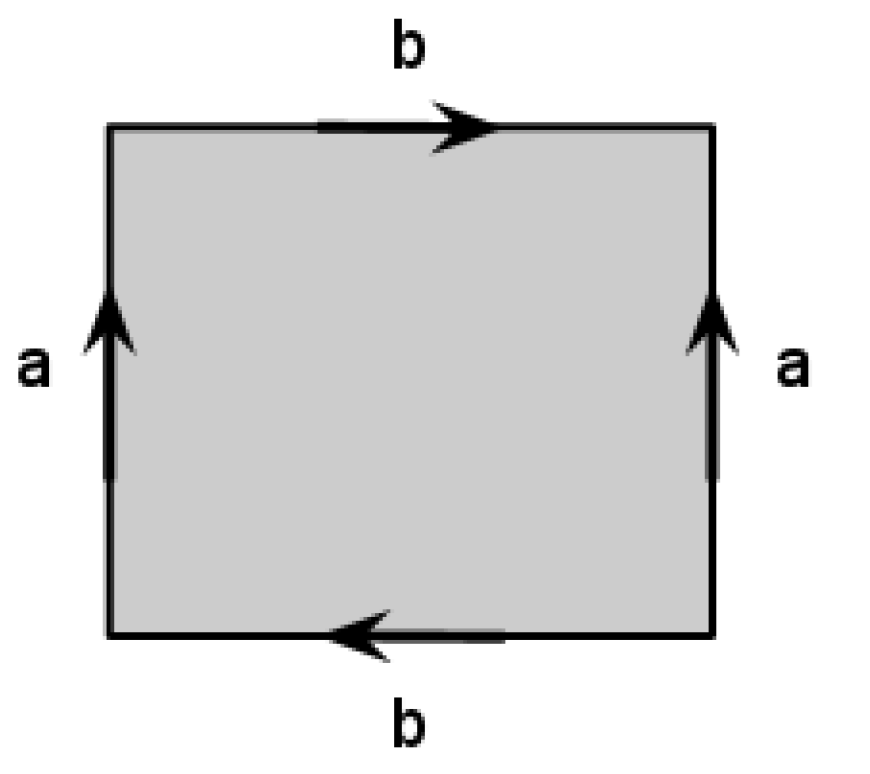
Describe the surface which we can get if we start with a rectangular sheet of paper, make a Moebius band by glueing the opposite sides in the opposite directions and then glue the other opposite sides of the paper band in the opposite direction as on the picture.
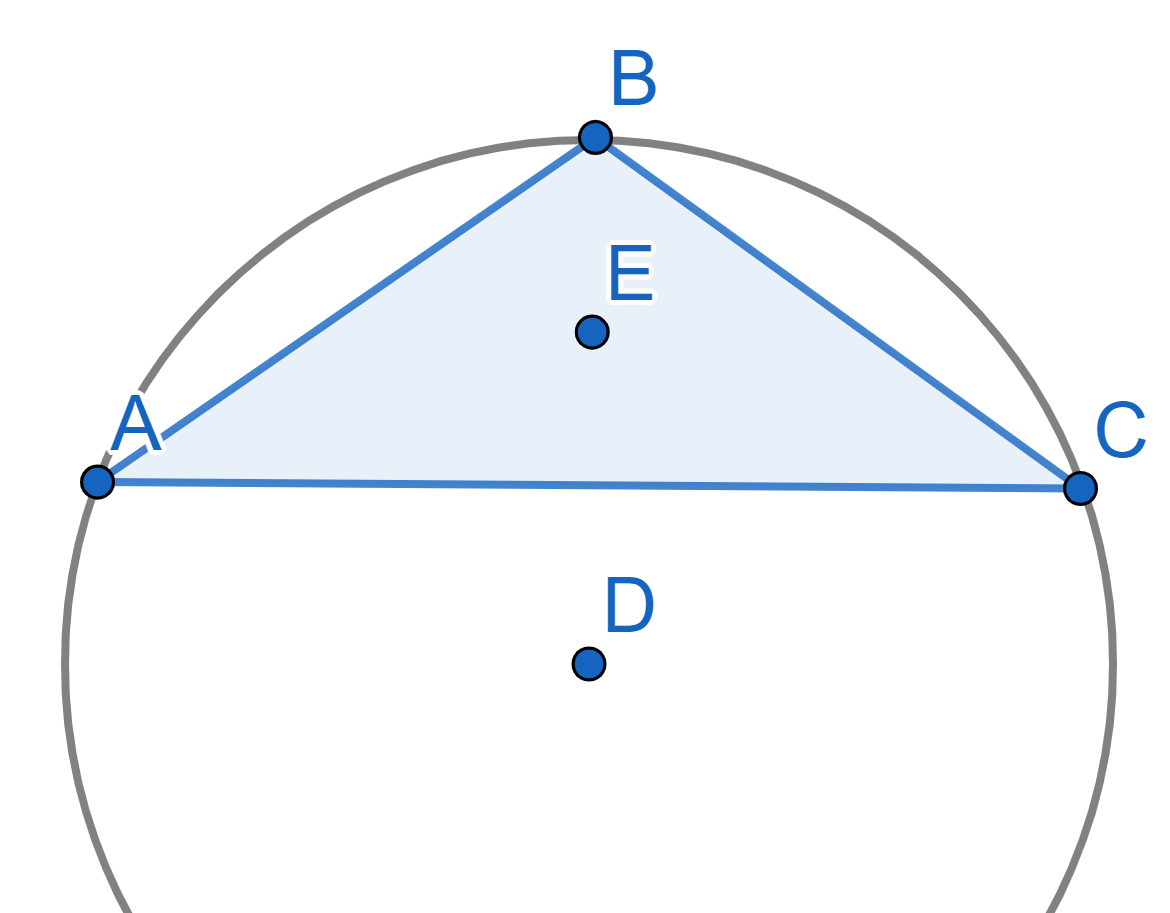
\(ABC\) is a triangle. The circumscribed circle is the circle that touches all three vertices of the triangle \(ABC\). It is also the smallest circle lying entirely outside the triangle. The center of the circumscribed circle is \(D\).
The inscribed circle is the circle which touches all three sides of the triangle \(ABC\). It is also the largest circle lying entirely inside the triangle. The center of the inscribed circle is \(E\).
The points \(D\) and \(E\) are symmetric with respect to the segment \(AC\). Find the angles of the triangle \(ABC\).
Scrooge McDuck has \(100\) golden coins on his office table. He wants to distribute them into \(10\) piles so that no two piles contain the same amount of coins. Moreover, no matter how you divide any of the piles into two smaller piles, among the resulting \(11\) piles there will be two with the same amount of coins. Find an example of how he could do that.
A parliament has 650 members. In this parliament there is only one house and every member has at most three enemies. We wish to split this parliament into two separate houses in such a way that each member will have at most one enemy in the same house as them. We assume that hard feelings among members of parliament are mutual, namely if \(A\) recognises \(B\) as their enemy, then \(B\) also recognises \(A\) as their enemy.
Is this splitting possible?