Problems

You and I are going to play a game. We have one million grains of sand in a bag. We take it in turns to remove $2$, $3$ or $5$ grains of sand from the bag. The first person that cannot make a move loses.

Would you go first?

For every natural number $k\ge 2$, find two combinations of $k$ real numbers such that their sum is twice their product.

Show that $n^2+n+1$ is not divisible by $5$ for any natural number $n$.

Prove the following identity for any three non-zero real numbers $a,b,c$: $$\frac{b}{2a}+\frac{c^2+ab}{4bc}-\left|\frac{c^2-ab}{4bc}\right|-\left|\frac{b}{2a}-\frac{c^2+ab}{4bc}+\left|\frac{c^2-ab}{4bc}\right|\right|=min\{\frac{b}{a},\frac{c}{b},\frac{a}{c}\}.$$

There are $n$ balls labelled 1 to $n$. If there are $m$ boxes labelled 1 to $m$ containing the $n$ balls, a legal position is one in which the box containing the ball $i$ has number at most the number on the box containing the ball $i+1$, for every $i$.

There are two types of legal moves: 1. Add a new empty box labelled $m+1$ and pick a box from box 1 to $m+1$, say the box $j$. Move the balls in each box with (box) number at least $j$ up by one box. 2. Pick a box $j$, shift the balls in the boxes with (box) number strictly greater than $j$ down by one box. Then remove the now empty box $m$.

Prove it is possible to go from an initial position with $n$ boxes with the ball $i$ in the box $i$ to any legal position with $m$ boxes within $n+m$ legal moves.

Given a natural number $n$, find a formula for the number of $k$ less than $n$ such that $k$ is coprime to $n$. Prove that the formula works.

A paper band of constant width is tied into a simple knot and tightened. Prove that the knot has the shape of a regular polygon.

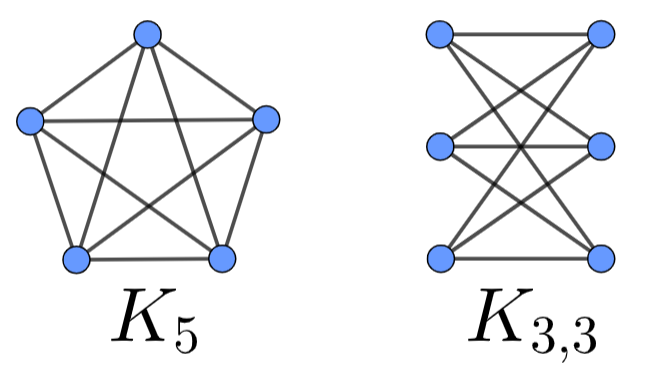
In the picture below you can see the graphs of $K_5$, the complete graph on $5$ vertices, and $K_{3,3}$, the complete bipartite graph on $3$ and $3$ vertices. A theorem states that these graphs cannot be embedded into plane, namely one cannot draw graphs $K_5$ and $K_{3,3}$ on a plane in such a way that there are no intersecting edges.
The question is: can you draw the graphs $K_5$ and $K_{3,3}$ without intersecting edges on a torus?

Is it possible to draw the graph $K_{3,3}$ without intersecting edges on a Moebius band?

Is it possible to link three rings together in such a way that they cannot be separate from each other, but if you remove any ring, then the other two will fall apart?