Problems
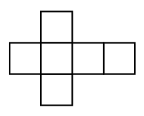
How can we tile the plane with this cube net?
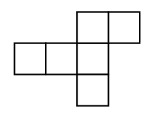
How can we tile the plane with this cube net?
Queen Hattius has two prisoners and gives them a puzzle. If they succeed, then she’ll let them free. She will randomly put a hat on each of their heads. The hats could be red or blue. They will simultaneously guess the colour of their own hat, and if at least one person is correct, then they win.
Each prisoner can only see the other prisoner’s hat - and not their own. The prisoners aren’t allowed to communicate once they’re wearing the hats, but they’re allowed to come up with a strategy before.
What should their strategy be?
Two children come in from playing outside, and both of their faces are muddy. Their dad says that at least one of their faces is muddy. He’ll repeat this phrase until all of the children with muddy faces have come forward. Assuming that the children can’t see or feel their own face, but that they’re perfect at logic, what happens?
Prince Hattius tests his three wisest men with a hat puzzle. He tells them that he’ll put a hat on each of their heads, either green or yellow. These wise men, used to such puzzles, know that in such a setup they’ll be able to see the colours of the other two hats, but not their own.
Then the Prince says that at least one hat is green and the winner is the first person to work out the colour of his own hat. He adds on that this puzzle is fair to all of them - what happens?
This time three children with muddy faces run into the house. They are perfect logicians, but don’t yet know whether their own faces are muddy - yet they can see the other childrens’ faces.
Their dad says that at least one of them has a muddy face. And that he’ll keep repeating sentence every ten seconds until all children with muddy faces step forward.
Show that all three step forward after he’s said the sentence for the third time.
Three witches (Rosalind, Sabrina and Theresa) are having a duel between themselves. Rosalind is the most accurate, hitting her target \(100\%\) of the time. Sabrina is moderately accurate, hitting her target \(\frac{2}{3}\) of the time. Theresa still needs to practise, so only hits her target \(\frac{1}{3}\) of the time.
The witches take it in turns to fire shots. Once a witch has been shot, she can no longer fire shots. To make it fair given their respective accuracies, they agree that the order will be Theresa, Sabrina and Rosalind, and then repeat in that order until the end.
Why is Theresa’s best strategy to fire her first shot away from both of her opponents?
Anna gives three pupils at We Solve Problems (Jacob, Leonhard and Sophie) the following puzzle. She writes down three different numbers on pieces of card, and asks each of the three pupils to hold up their cards. She asks them to do this in such a way that they can’t see their own card, but that the other two people can see theirs.
Sophie sees that Jacob has \(8\) and
Leonhard has \(12\). Anna then tells
them that two of the cards add up to the third.
Sophie says ‘I don’t know my number.’
Leonhard says ‘I also don’t know my number.
What is Sophie’s number?
One of three friends gives the other two a puzzle. Mario says “I’ve thought of two different one-digit numbers. When you multiply these two numbers, the last digit of that is the same as the last digit of Lizzie’s house number. What’s the sum of these two one-digit numbers?"
Ioannis says “I don’t know Lizzie’s house number"
Then Lizzie says “Well, obviously I know my own house number. And now I’ve worked out the sum of the two numbers."
Finally Ioannis says “Ahh, I didn’t know the sum before, but now I
know the sum."
What’s the sum?
Princess Hattius invites several of the court’s Logicians to the forest. She tells them she’ll put a hat on each of their heads. The logicians will be able to see the colours of others’ hats, but not their own. The logicians are used to such puzzles, and so know that they’re not allowed to take off their own hat, or look in a mirror, or lake reflection. They are only allowed to work out their hat’s colour by logic and deduction.
The princess tells them she’ll ring a bell every minute, and that once a logician has worked out his or her own hat’s colour, then they should stand up and leave at the next bell. She also tells them that every colour appears twice, so each logician sees someone else with the same colour hat of their own.
What happens?