Problems
In chess, knights can move one square in one direction and two squares in a perpendicular direction. This is often seen as an ‘L’ shape on a regular chessboard. A closed knight’s tour is a path where the knight visits every square on the board exactly once, and can get to the first square from the last square.
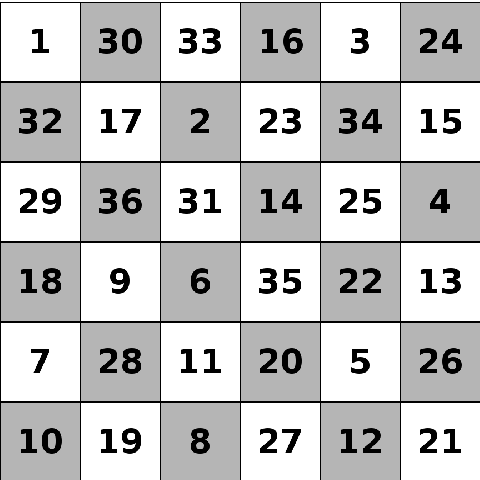
This is a closed knight’s tour on a \(6\times6\) chessboard.
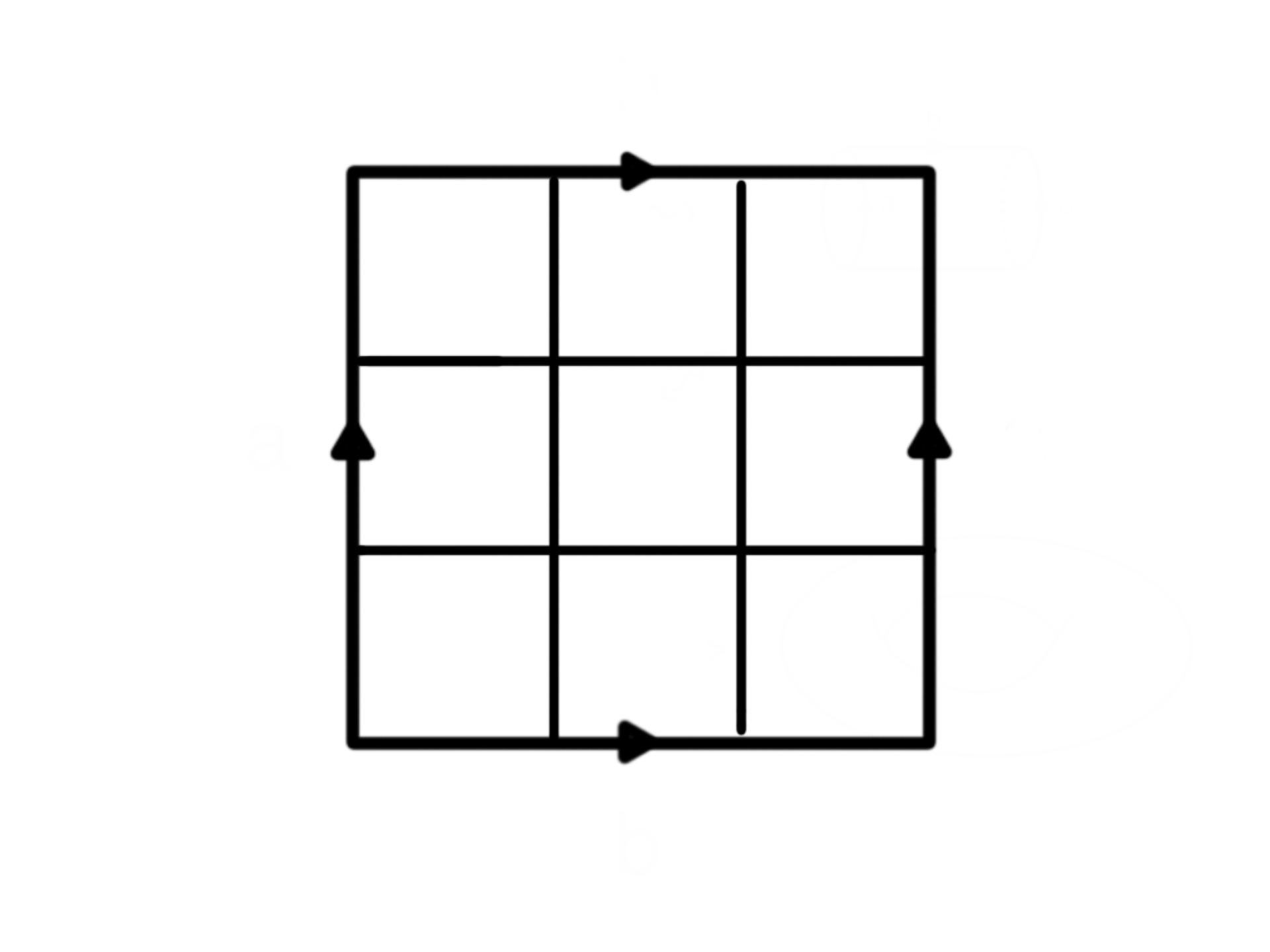
Can you draw a closed knight’s tour on a \(3\times3\) torus? That is, a \(3\times3\) square with both pairs of opposite sides identified in the same direction, like the diagram below.
You may remember the game Nim. We will now play a slightly modified version, called Thrim. In Thrim, there are two piles of stones (or any objects of your choosing), one of size \(1\) and the other of size \(5\). Whoever takes the last stone wins. The players take turns to remove stones - they can only remove stones from one pile at a time, and they can remove at most \(3\) stones at a time. Does the player going first or the player going second have a winning strategy?
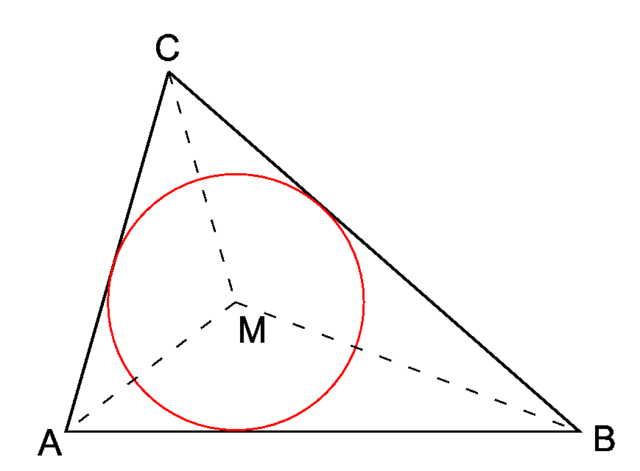
A circle is inscribed in a triangle (that is, the circle touches the sides of the triangle on the inside). Let the radius of the circle be \(r\) and the perimeter of the triangle be \(p\). Prove that the area of the triangle is \(\frac{pr}{2}\).
We meet a group of people, all of whom are either knights or liars. Knights always tell the truth and liars always lie. Prove that it’s impossible for someone to say “I’m a liar".
We’re told that Leonhard and Carl are knights or liars (the two of them could be the same or one of each). They have the following conversation.
Leonhard says “If \(49\) is a prime number, then I am a knight."
Carl says “Leonhard is a liar".
Prove that Carl is a liar.
Today we will solve some logic problems. This time, we are visiting a strange planet. This planet is inhabited by two kinds of aliens, Cricks and Goops. The physical differences between them are not enough for a human being to distinguish them, but they have another remarkable feature. They can only ask questions. Cricks can only ask questions whose answer is yes, while Goops can only ask questions whose answer is no.
Let \(p\) be a prime number greater than \(3\). Prove that \(p^2-1\) is divisible by \(12\).
In this sheet, we will look at basic counting problems. The fundamental principle is quite simple. If you have two independent choices to make, then the number of options for making both choices is calculated by multiplying the number of options for each choice.
An issue we frequently run into is that of overcounting. This means we count the same thing more than once. In the examples and problems today, you will see various ideas that we can use to correct for overcounting, or for avoiding it.
From the examples above, we see that we often need to pick \(k\) objects from \(n\) objects where the order of the \(k\) objects is ignored. The number of ways to pick them is notated with the special symbol \(\binom{n}{k}\), pronounced "\(n\) choose \(k\)". What’s a formula for \[\binom{n}{k}\]?
By checking which of the following numbers are divisible by \(11\): \[121,\,143,\,286,\,235,\,473,\,798,\,693,\,576,\,748\] can you find and prove a condition that is enough to guarantee a number is divisible by \(11\)?