Problems

Given an endless piece of chequered paper with a cell side equal to one. The distance between two cells is the length of the shortest path parallel to cell lines from one cell to the other (it is considered the path of the center of a rook). What is the smallest number of colors to paint the board (each cell is painted with one color), so that two cells, located at a distance of 6, are always painted with different colors?

\(f(x)\) is an increasing function defined on the interval \([0, 1]\). It is known that the range of its values belongs to the interval \([0, 1]\). Prove that, for any natural \(N\), the graph of the function can be covered by \(N\) rectangles whose sides are parallel to the coordinate axes so that the area of each is \(1/N^2\). (In a rectangle we include its interior points and the points of its boundary).

A group of numbers \(A_1, A_2, \dots , A_{100}\) is created by somehow re-arranging the numbers \(1, 2, \dots , 100\).

100 numbers are created as follows: \[B_1=A_1,\ B_2=A_1+A_2,\ B_3=A_1+A_2+A_3,\ \dots ,\ B_{100} = A_1+A_2+A_3\dots +A_{100}.\]

Prove that there will always be at least 11 different remainders when dividing the numbers \(B_1, B_2, \dots , B_{100}\) by 100.

There are 68 coins, and it is known that any two coins differ in weight. With 100 weighings on a two-scales balance without weights, find the heaviest and lightest coin.

a) Give an example of a positive number \(a\) such that \(\{a\} + \{1 / a\} = 1\).

b) Can such an \(a\) be a rational number?

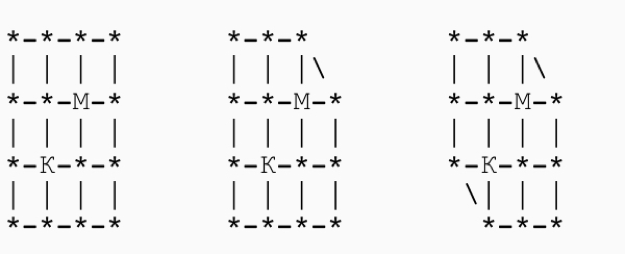
A cat tries to catch a mouse in labyrinths A, B, and C. The cat walks first, beginning with the node marked with the letter “K”. Then the mouse (from the node “M”) moves, then again the cat moves, etc. From any node the cat and mouse go to any adjacent node. If at some point the cat and mouse are in the same node, then the cat eats the mouse.

Can the cat catch the mouse in each of the cases A, B, C?

Two play a game on a chessboard \(8 \times 8\). The player who makes the first move puts a knight on the board. Then they take turns moving it (according to the usual rules), whilst you can not put the knight on a cell which he already visited. The loser is one who has nowhere to go. Who wins with the right strategy – the first player or his partner?

Two players in turn increase a natural number in such a way that at each increase the difference between the new and old values of the number is greater than zero, but less than the old value. The initial value of the number is 2. The winner is the one who can create the number 1987. Who wins with the correct strategy: the first player or his partner?

a) The vertices (corners) in a regular polygon with 10 sides are colored black and white in an alternating fashion (i.e. one vertex is black, the next is white, etc). Two people play the following game. Each player in turn draws a line connecting two vertices of the same color. These lines must not have common vertices (i.e. must not begin or end on the same dot as another line) with the lines already drawn. The winner of the game is the player who made the final move. Which player, the first or the second, would win if the right strategy is used?

b) The same problem, but for a regular polygon with 12 sides.

We consider a sequence of words consisting of the letters “A” and “B”. The first word in the sequence is “A”, the \(k\)-th word is obtained from the \((k-1)\)-th by the following operation: each “A” is replaced by “AAB” and each “B” by “A”. It is easy to see that each word is the beginning of the next, thus obtaining an infinite sequence of letters: AABAABAAABAABAAAB...

a) Where in this sequence will the 1000th letter “A” be?

b) Prove that this sequence is non-periodic.