Problems
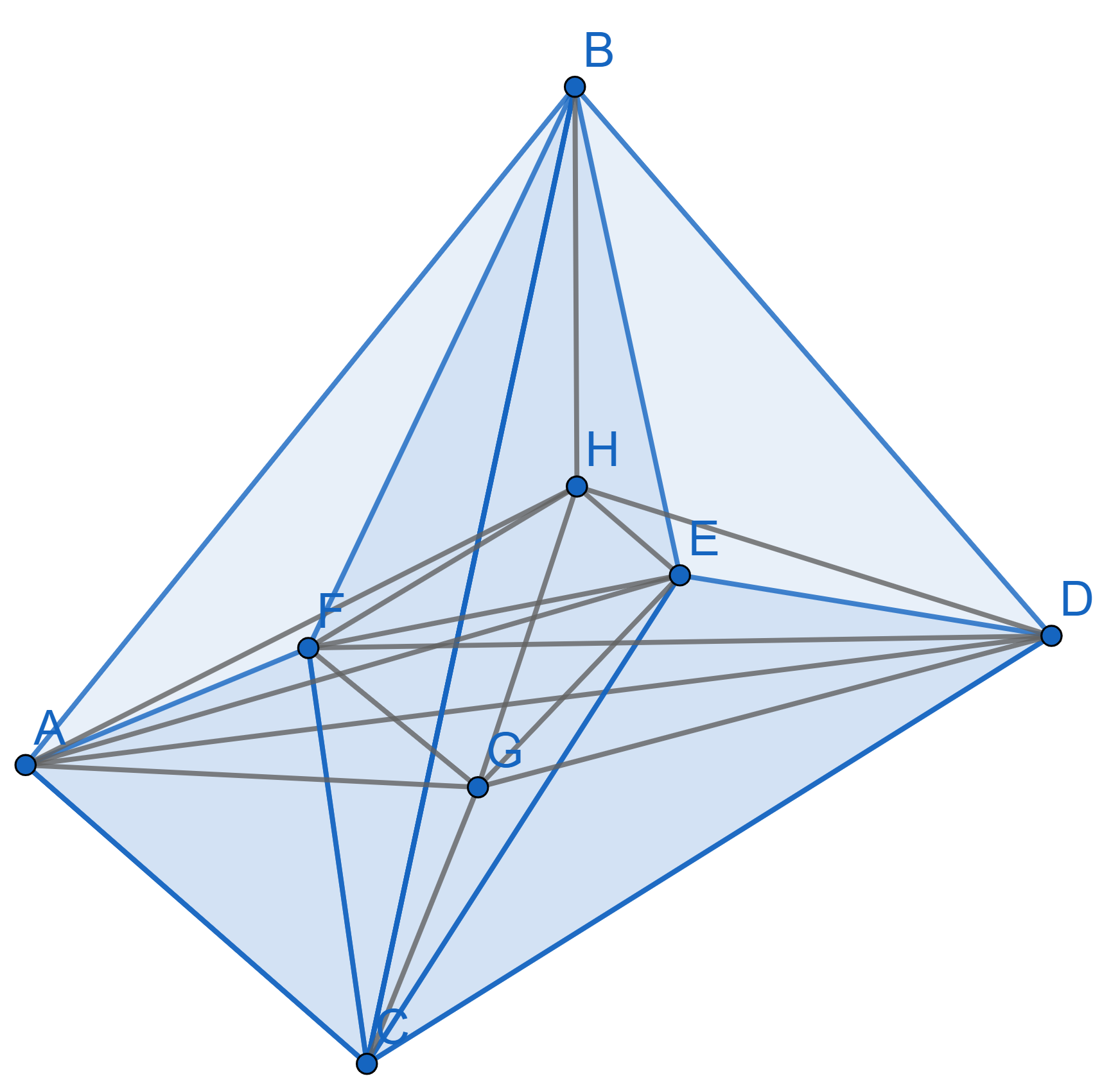
Draw a Sperner’s coloring for the following \(3\)-dimensional simplex. The blue segments are visible, the grey ones are inside the tetrahedron. The point \(F\) is on the face \(ABC\), point \(E\) is on the face \(BCD\), point \(G\) is on the face \(ACD\) and the point \(H\) is on the face \(ABD\).
Four football teams play in a tournament. There’s the Ulams (\(U\)), the Vandermondes (\(V\)), the Wittgensteins (\(W\)) and the Xenos (\(X\)). Each team plays every other team
exactly once, and matches can end in a draw.
If a game ends in a draw, then both teams get \(1\) point. Otherwise, the winning team gets
\(3\) points and the losing team gets
\(0\) points. At the end of the
tournament, the teams have the following points totals: \(U\) has \(7\), \(V\)
has \(4\), \(W\) has \(3\) and \(X\) has \(2\).
Work out the results of each match, including showing that there’s no other way the results could have played out.
Naomi and Rory get tired of playing Nim, so decide to change the rules to mix it up. They call their new variant ‘Wonim’. There are two piles of four matchsticks each. They take it in turns to take matchsticks. Each player has to take at least one matchstick, and they can take as many as they like from one pile only.
Except, their new rule is that a player cannot take the same number of matchsticks that their opponent just did. For example, consider Wonim(\(5\),\(10\)). If Naomi’s first move is to take \(4\) matchsticks from the pile of size \(5\), turning the game to Wonim(\(1\),\(10\)), then Rory cannot take \(4\) matchsticks - he has to take more or less. A player loses if they cannot go - this can happen if there are no matchsticks left, or if there are matchsticks left, but they can’t take any since their opponent took that number. e.g. Wonim(\(1\),\(1\)), Naomi takes \(1\), Rory faces Wonim(\(1\)) but can’t move since he’s not allowed to take \(1\).
In the game Wonim(\(4\),\(4\)) with Naomi going first, who has the winning strategy?
Prove that \(n^{n+1}>(n+1)^n\) for integers \(n\ge3\).
What is the following as a single fraction? \[\frac{1}{1\times2}+\frac{1}{2\times3}+\frac{1}{3\times4}+...+\frac{1}{98\times99}+\frac{1}{99\times100}.\]
Prove that \(3\) always divides \(2^{2n}-1\), where \(n\) is a positive integer.
Adi and Maxim play a game. There are \(100\) sweets in a bowl, and they each take in turns to take either \(2\), \(3\) or \(4\) sweets. Whoever cannot take any more sweets (since the bowl is empty, or there’s only \(1\) left) loses.
Maxim goes first - who has the winning strategy?
Michelle and Mondo play the following game, with Michelle going first. They start with a regular polygon, and take it in turns to move. A move is to pick two non-adjacent points in one polygon, connect them, and split that polygon into two new polygons. A player wins if their opponent cannot move - which happens if there are only triangles left. See the diagram below for an example game with a pentagon. Prove that Michelle has the winning strategy if they start with a decagon (\(10\)-sided polygon).
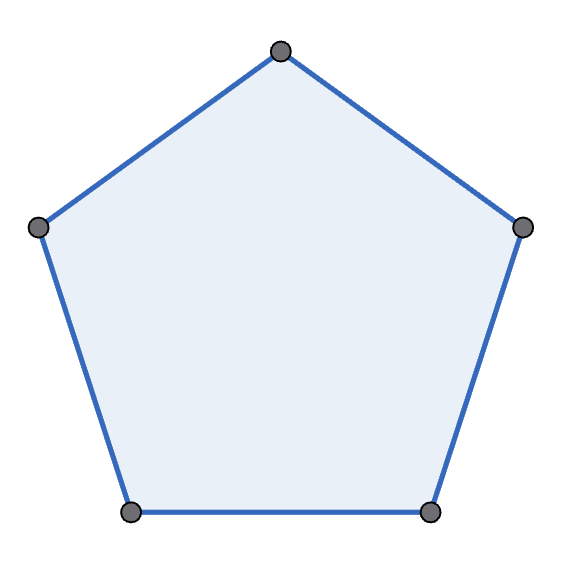
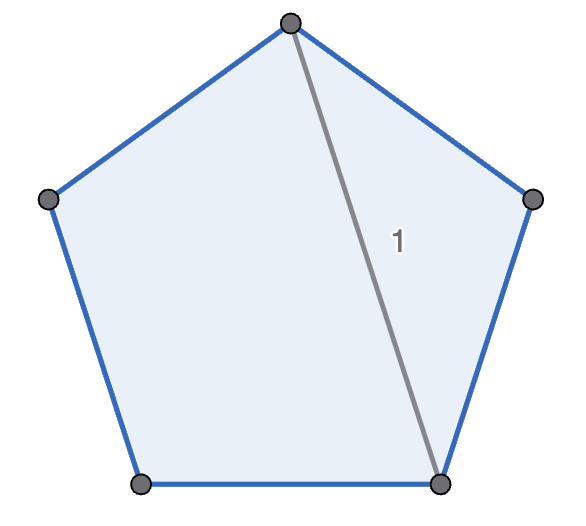
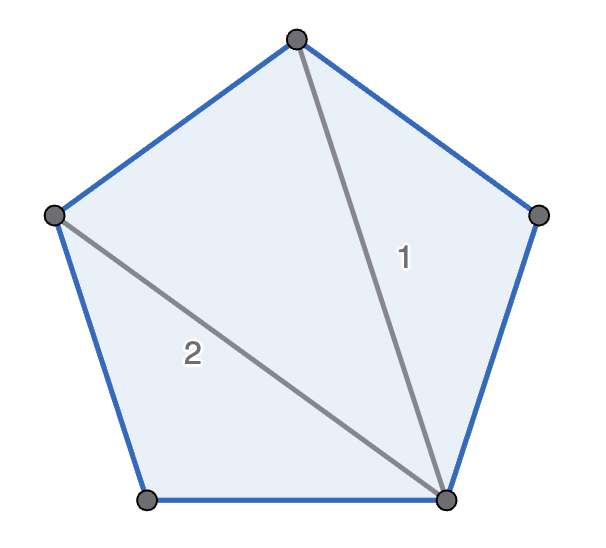
Let \(n\) be a positive integer. Show that \(1+3+3^2+...+3^{n-1}+3^n=\frac{3^{n+1}-1}{2}\).
Show that all integers greater than or equal to \(8\) can be written as a sum of some \(3\)s and \(5\)s. e.g. \(11=3+3+5\). Note that there’s no way to write \(7\) in such a way.