Problems
During the ball every young man danced the waltz with a girl, who was either more beautiful than the one he danced with during the previous dance, or more intelligent, but most of the men (at least 80%) – with a girl who was at the same time more beautiful and more intelligent. Could this happen? (There was an equal number of boys and girls at the ball.)
A \(1 \times 10\) strip is divided into unit squares. The numbers \(1, 2, \dots , 10\) are written into squares. First, the number 1 is written in one square, then the number 2 is written into one of the neighboring squares, then the number 3 is written into one of the neighboring squares of those already occupied, and so on (the choice of the first square is made arbitrarily and the choice of the neighbor at each step). In how many ways can this be done?
4 points \(a, b, c, d\) lie on the segment \([0, 1]\) of the number line. Prove that there will be a point \(x\), lying in the segment \([0, 1]\), that satisfies \[\frac{1}{ | x-a |}+\frac{1}{ | x-b |}+\frac{1}{ | x-c |}+\frac{1}{ | x-d |} < 40.\]
Some points with integer co-ordinates are marked on a Cartesian plane. It is known that no four points lie on the same circle. Prove that there will be a circle of radius 1995 in the plane, which does not contain a single marked point.
Imagine an infinitely large sheet of paper with a square drawn on it. Somewhere on the paper, a point \(P\) is marked with ink that is invisible to you. However, a friend with a special pair of glasses can see the point.
We are allowed to draw straight lines on the paper, and for each line, our friend will tell us on which side of the line the point \(P\) is. (If \(P\) is exactly on the line, they will say so.) For example, on this picture, our friend would say that the point \(P\) is above the line we’ve drawn:
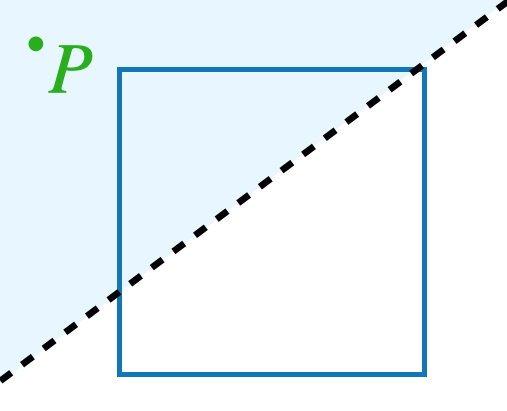
What is the smallest number of such questions that are needed in order to be certain whether \(P\) lies inside the square? Explain why it cannot be done in less questions then you are suggesting.
Let \(n\) numbers are given together with their product \(p\). The difference between \(p\) and each of these numbers is an odd number.
Prove that all \(n\) numbers are irrational.
Two play tic-tac-toe on a \(10 \times 10\) board according to the following rules. First they fill the whole board with noughts and crosses, putting them in turn (the first player puts crosses, their partner – noughts). Then two numbers are counted: \(K\) is the number of five consecutively standing crosses and \(H\) is the number of five consecutively standing zeros. (Five, standing horizontally, vertically and parallel to the diagonal are counted, if there are six crosses in a row, this gives two fives, if there are seven, then three, etc.). The number \(K-H\) is considered to be the winnings of the first player (the losses of the second).
a) Does the first player have a winning strategy?
b) Does the first player have a non-losing strategy?
Some real numbers \(a_1, a_2, a_3,\dots ,a _{2022}\) are written in a row. Prove that it is possible to pick one or several adjacent numbers, so that their sum is less than 0.001 away from a whole number.
a) Could an additional \(6\) digits be added to any \(6\)-digit number starting with a \(5\), so that the \(12\)-digit number obtained is a complete square?
b) The same question but for a number starting with a \(1\).
c) Find for each \(n\) the smallest \(k = k (n)\) such that to each \(n\)-digit number you can assign \(k\) more digits so that the resulting \((n + k)\)-digit number is a complete square.
Initially, on each cell of a \(1 \times n\) board a checker is placed. The first move allows you to move any checker onto an adjacent cell (one of the two, if the checker is not on the edge), so that a column of two pieces is formed. Then one can move each column in any direction by as many cells as there are checkers in it (within the board); if the column is on a non-empty cell, it is placed on a column standing there and unites with it. Prove that in \(n - 1\) moves you can collect all of the checkers on one square.